leetcode刷题--数组类-编程知识

文章目录

- - 1. 485 最大连续1的个数
  - 2. 495 提莫攻击
  - 3. 414 第三大的数
  - 4. 628 三个数的最大乘积
  - 5. 645 错误的集合
  - 6. 697 数组的度
  - 7. 448 找到所有数组中消失的数字
  - 9. 41 缺失的第一个正数
  - 10. 274 H指数
  - 11. 453 最小操作次数使得数组元素相等
  - 12. 665 非递减数列
  - 13. 283 移动零
  - 14. 118 杨辉三角
  - 15. 119 杨辉三角II
  - 16. 661 图片平滑器
  - 17. 598 范围求和 II
  - 18. 419 甲板上的战舰
  - 19. 189 轮转数组
  - 20. 396 旋转函数
  - 21. 54 螺旋矩阵
  - 22. 59 螺旋矩阵II
  - 23. 498 对角线遍历
  - 24. 566 重塑矩阵
  - 25. 73 矩阵置零
  - 26.289 生命游戏
  - 27. 303 区域和检索--数组不可变
  - 28. 304 二维区域和检索-矩阵不可变
  - 29. 238 除自身以外数组的乘积

数组的遍历 485、495、414、628

统计数组中的元素 645、697、448、442、41、274

数组的改变、移动 453、665、283

二维数组及滚动数组 118、119、661、598、419

数组的旋转 189、396

特定顺序遍历二维数组 54、59、498

二维数组变换 566、48、73、289

前缀和数组 303、304、238

1. 485 最大连续1的个数

解法：很简单的一次遍历

为了得到数组中最大的连续1的个数，使用cnt记录当前连续1的个数，使用max记录最大连续的1。当遇到1时候，cnt+1，当碰到的不是1时，需要比较cnt和max之间的值，判断是否更新max值，并且将cnt置为0。

最后要注意的是，当循环遍历结束之后，还需要比较一次cnt和max。因为数组的最后一位数有可能是1，且最长连续1的子数组可能出现在数组的末尾。

代码：

//
// Created by 高森森 on 2022/9/19.
//#ifndef LEETCODE_SOLUTION_1_H
#define LEETCODE_SOLUTION_1_H
#include<bits/stdc++.h>
using namespace std;class solution_1 {
public:
int findMaxConsecutiveOnes(vector<int>& nums) {
int cnt=0;
int max=0;
for(int i=0;i<nums.size();i++){
if(nums[i]==1){
cnt++;
}
else{
if(cnt>max){
max=cnt;
}
cnt=0;
}
}
if(cnt>max){
max=cnt;
}
return max;
}
};#endif //LEETCODE_SOLUTION_1_H

时间复杂度：O（n）n是数组的长度

空间复杂度：O（1）

2. 495 提莫攻击

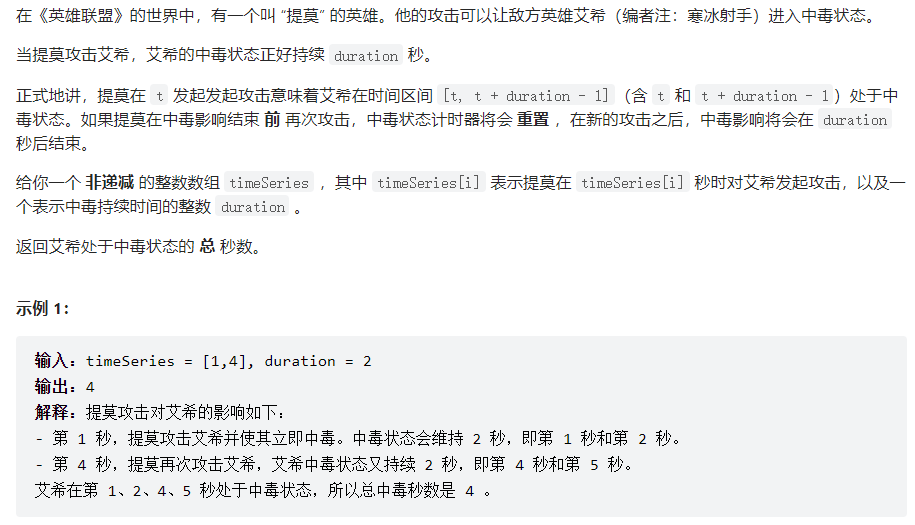
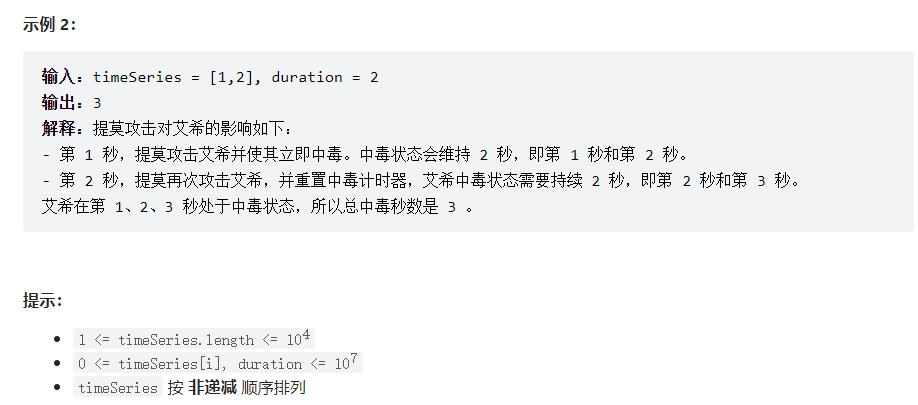
解法：简单的模拟题，遍历一遍数组，每次保存上一次结束的时间last，ans用于累积加和。当last小于当前的时间时，说明不会冲突，ans=ans+duration;当last>=当前的时间时，说明时间有重叠，ans+=当前结束时间-上一个结束时间

代码：

class Solution {
public:    int findPoisonedDuration(vector<int>& timeSeries, int duration) {int last=-1;int ans=0;for(int i=0;i<timeSeries.size();i++){if(last<timeSeries[i]){last=timeSeries[i]+duration-1;ans+=duration;}else{ans+=timeSeries[i]+duration-1-last;last=timeSeries[i]+duration-1;}}return ans;}
};

3. 414 第三大的数

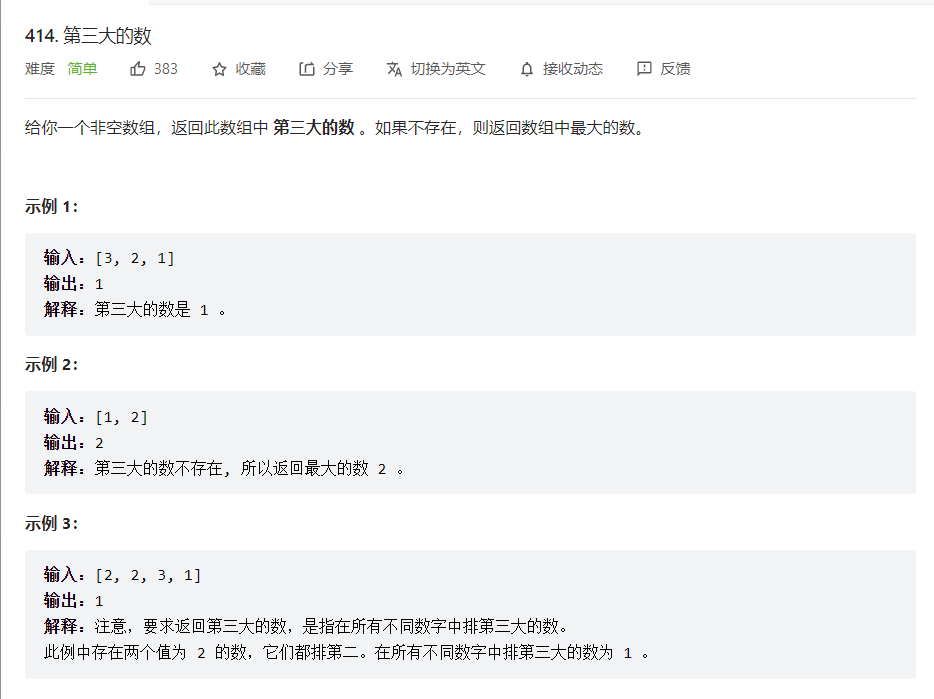
解法：采用有序数组的形式，遍历数组，有一个有序的集合维护数组中的前三大的数。遍历每一个数，将其插入有序集合，因为set有序集合是自动排序的，自动按照从小到大的顺序排序，如果有序集合的大小超过3。那么就删除最小的元素，相当于维护一个容量为3的队列。遍历结束后，如果有序集合的大小是3，最小值就是第三大的数字，如果有序集合没有3个，那么就返回有序集合中最大值。

代码：

class solution_3 {
public:int thirdMax(vector<int>& nums) {set<int>maxsize;for(int i=0;i<nums.size();i++){maxsize.insert(nums[i]);if(maxsize.size()>3){maxsize.erase(maxsize.begin());}}return maxsize.size()==3?*maxsize.begin():*maxsize.rbegin();}
};

时间复杂度：O（n），其中n是数组nums的长度。因为有序集合大小至多为3，插入和删除的时间复杂度可以看作O（1）

空间复杂度：O（1）

4. 628 三个数的最大乘积

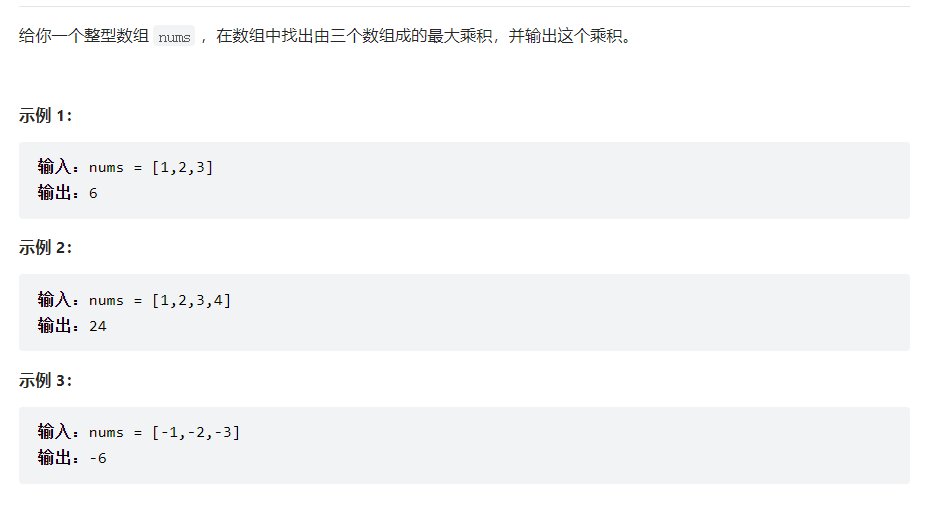
解法：首先分析以下情况，数组中数组的个数大于等于3。1.如果数组全部为非负数数，那么最大值为最大的三个，如果数组中全部为负数，那么最大值也为最大的三个。如果数组中既有正数又有负数，最大值可能是最小的两个负数*最大的正数，也有可能是最大的三个正数。需要取两者最大值。

代码：

class solution_4 {
public:int maximumProduct(vector<int>& nums) {sort(nums.begin(),nums.end());int result=0;int n=nums.size();if(*(nums.end()-1)>=0&&*nums.begin()>=0){result=nums[n-1]*nums[n-2]*nums[n-3];}else if(*nums.begin()<0&&*(nums.end()-1)<0){result=nums[n-1]*nums[n-2]*nums[n-3];}else{int a=nums[0]*nums[1]*nums[n-1];int b=nums[n-1]*nums[n-2]*nums[n-3];result=a>b?a:b;}return result;}
};

时间复杂度：O（nlogn）为排序的复杂度

空间复杂度：O（nlogn）为排序的空间

5. 645 错误的集合

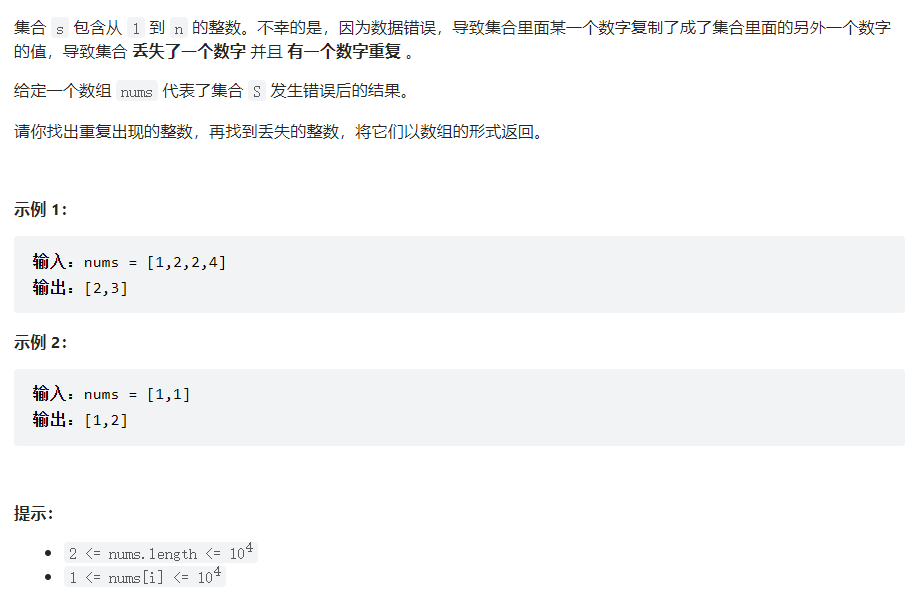
解法：因为包含1-n个数字，并且每个数字只能出现1遍，所以可以遍历nums数组，将其存入集合set中，如果set中的key已经存在，说明数字重复。同时set默认升序排序，遍历1-n，检查1-n数字是否在set中存在，若不存在，则缺少的数字找到。

代码：

class solution_5 {
public:vector<int> findErrorNums(vector<int>& nums) {int n=nums.size();int r1,r2;set<int>t;for(int i=0;i<nums.size();i++){if(t.count(nums[i])==0){t.insert(nums[i]);}else{r1=nums[i];}}for(int i=1;i<=n;i++){if(t.count(i)==0){r2=i;break;}}return {r1,r2};}
};

时间复杂度：O（n）

空间复杂度:O（n）

解法2：数组异或

数组的异或求解

6. 697 数组的度

解法：

题目可以分成两个部分求解，首先求得原数组的度，然后求得与原数组有相同的度的最短子数组。

求原数组的度，就是求各个元素出现的次数，可以用map计数，map中的key是元素，value是该元素出现的次数。因此，字典中所有的value的最大值就是数组的度degree。
求得最大度之后，如果求与度相同的最短子数组

分析上面的示例1：[1,2,2,3,1]，最短子数组为[2,2]。因为最短子数组中必须包括度的所有元素，所以最短的子数组的大小与度的元素的最早和最迟的出现位置有关。因此度最大的数字有1和2.

包含2的最短子数组为[2,2]，包含1的最短子数组为[1,2,2,3,1]。所以最短子数组为包含度最大元素的最短子数组大小的最小值。

示例2：[1,2,2,3,1,4,2]，度为3，元素为2。包含2的最短子数组为[2,2,3,1,4,2]。

因此可以得到规律，包含某个元素的最短子数组的长度为，该数字最后一次出现的位置索引-第一次出现的位置索引+1。

代码：
```
class solution_6 {
public:int findShortestSubArray(vector<int>& nums) {unordered_map<int,int>left,right,counter;int degree=0;for(int i=0;i<nums.size();i++){if(left.count(nums[i])==0){left.insert(make_pair(nums[i],i));}right[nums[i]]=i;counter[nums[i]]++;degree=max(degree,counter[nums[i]]);}int res=INT_MAX;//得到最大的度for(auto it=counter.begin();it!=counter.end();it++){if(it->second==degree){res=min(right[it->first]-left[it->first]+1,res);}}return res;}
};
```
时间复杂度：O（N）

空间复杂度：O（N）

7. 448 找到所有数组中消失的数字

解法：

方法一：遍历vector数组，将所有的数字都保存在set中，因为set的自动重复的功能，得到的是所有的数字。

遍历1-n,如果数字在set中不存在，则输出。

class solution_7 {
public:vector<int> findDisappearedNumbers(vector<int>& nums) {set<int>p;int n=nums.size();for(int i=0;i<n;i++){p.insert(nums[i]);}vector<int>res;for(int i=1;i<=n;i++){if(p.count(i)==0){res.push_back(i);}}return res;}
};

时间复杂度：O（n）

空间复杂度：O(n)

方法二：官方解法就地修改

我们可以用一个哈希表记录数组nums 中的数字，由于数字范围均在 [1,n] 中，记录数字后我们再利用哈希表检查 [1,n] 中的每一个数是否出现，从而找到缺失的数字。

由于数字范围均在 [1,n] 中，我们也可以用一个长度为 n 的数组来代替哈希表。这一做法的空间复杂度是 O(n) 的。我们的目标是优化空间复杂度到 O(1)。

注意到 nums 的长度恰好也为 n，能否让 nums 充当哈希表呢？

由于nums 的数字范围均在[1,n] 中，我们可以利用这一范围之外的数字，来表达「是否存在」的含义。

具体来说，遍历 nums，每遇到一个数 x，就让 nums[x−1] 增加 n。由于 nums 中所有数均在[1,n] 中，增加以后，这些数必然大于 n。最后我们遍历 nums，若 nums[i] 未大于 n，就说明没有遇到过数 i+1。这样我们就找到了缺失的数字。

注意，当我们遍历到某个位置时，其中的数可能已经被增加过，因此需要对 n 取模来还原出它本来的值。

class Solution {
public:vector<int> findDisappearedNumbers(vector<int>& nums) {int n = nums.size();for (auto& num : nums) {int x = (num - 1) % n;nums[x] += n;}vector<int> ret;for (int i = 0; i < n; i++) {if (nums[i] <= n) {ret.push_back(i + 1);}}return ret;}
};

时间复杂度：O（n）

空间复杂度：O（1）

9. 41 缺失的第一个正数

解法：当然暴力解法也能够解决问题，但是不满足在时间复杂度为O（n）。

我们还可以把每个元素存放到对应的位置，比如1存放到数组的第一个位置，3存放到数组的第3个位置，如果是非正数或者大于数组的长度的值，我们不做处理，最后在遍历一遍数组，如果位置不正确，说明这个位置没有这个数，我们就直接返回。

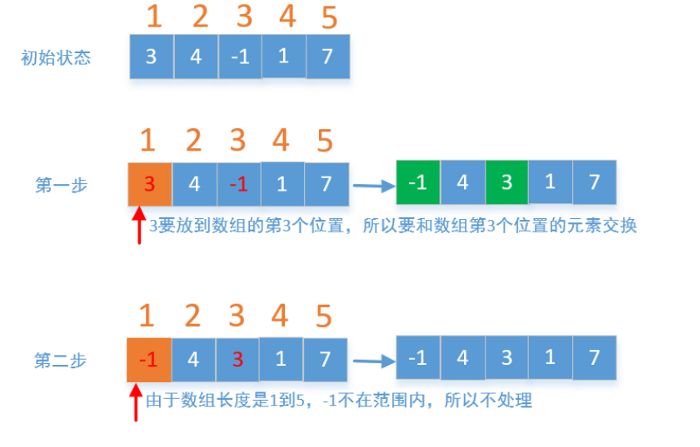
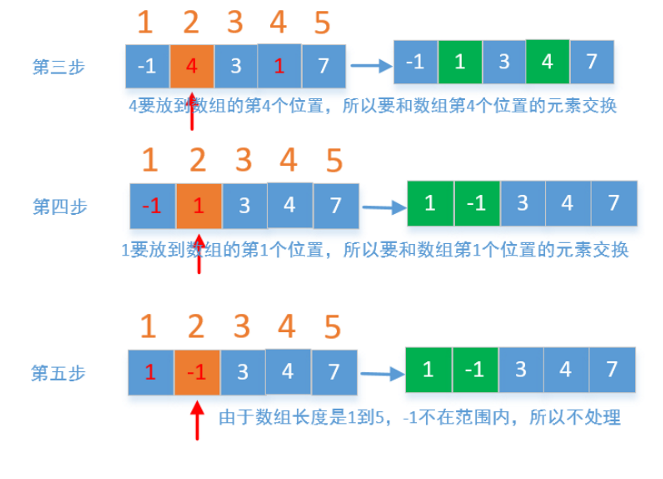
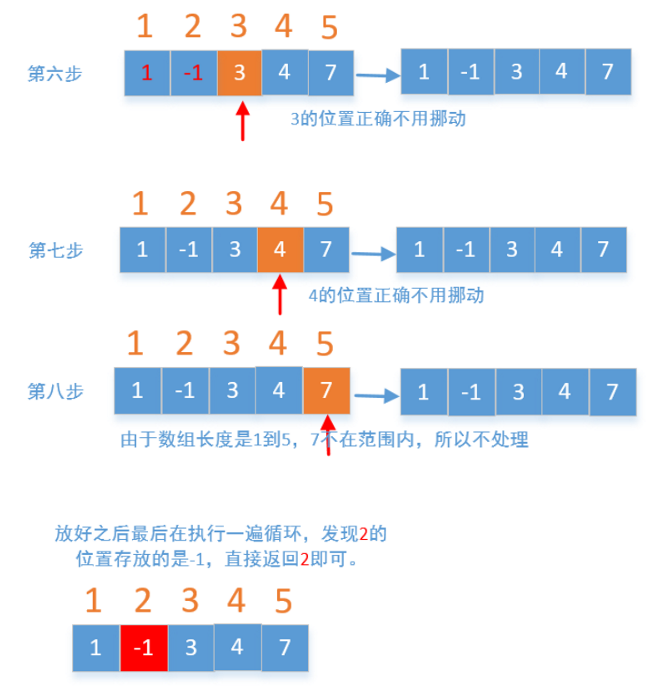
代码：

  int firstMissingPositive(vector<int>& nums) {
int index=0;
while(index<nums.size()){
int tmp=nums[index];
if(tmp<=0||tmp>=nums.size()) {
index++;
}
else{
if(tmp==nums[tmp-1]){
index++;
continue;
}
int cnt=nums[tmp-1];
nums[tmp-1]=nums[index];
nums[index]=cnt;}
}
for(int i=0;i<nums.size();i++){
if(nums[i]!=i+1){
return i+1;
}
}
return nums.size()+1;
}

时间复杂度：O（n）

空间复杂度：O（1）

10. 274 H指数

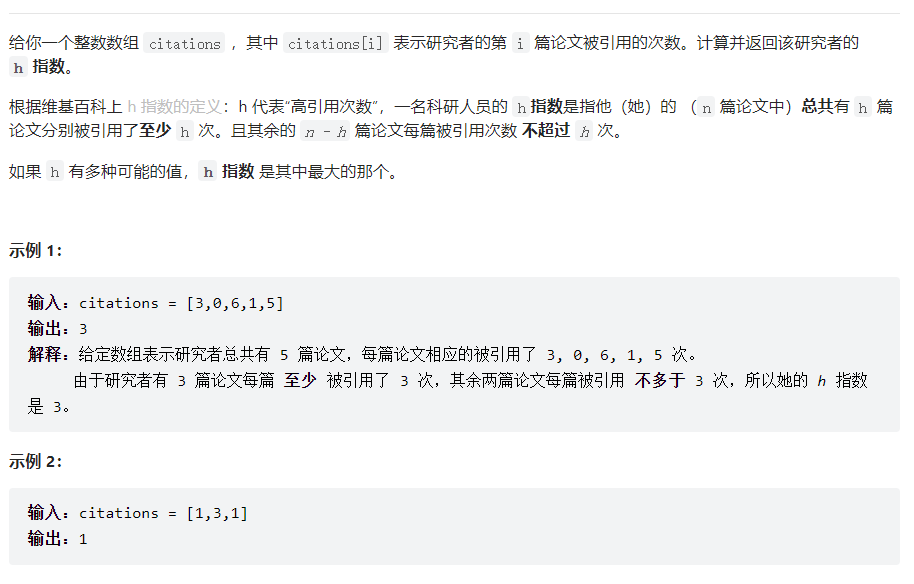
解法一：排序

首先我们可以将初始的}H 指数 h 设为 0，然后将引用次数排序，并且对排序后的数组从大到小遍历。

根据H 指数的定义，如果当前H 指数为 h 并且在遍历过程中找到当前值citations[i]>h，则说明我们找到了一篇被引用了至少 h+1 次的论文，所以将现有的 h 值加 1。继续遍历直到 h 无法继续增大。最后返回 h 作为最终答案。

class solution_9 {
public:int hIndex(vector<int>& citations) {sort(citations.begin(),citations.end());int n=citations.size()-1;int h=0;while(n>=0&&citations[n]>h){h++;n--;}return h;}
};

时间复杂度：O（nlogN）

空间复杂度: O（log n）排序的空间复杂度

解法二：计数排序

根据上述解法我们发现，最终的时间复杂度与排序算法的时间复杂度有关，所以我们可以使用计数排序算法，新建并维护一个数组 counter 用来记录当前引用次数的论文有几篇。

根据定义，我们可以发现 H 指数不可能大于总的论文发表数，所以对于引用次数超过论文发表数的情况，我们可以将其按照总的论文发表数来计算即可。这样我们可以限制参与排序的数的大小为 [0,n]（其中 n 为总的论文发表数），使得计数排序的时间复杂度降低到 O(n)。

最后我们可以从后向前遍历数组 counter，对于每个 0≤i≤n，在数组 counter 中得到大于或等于当前引用次数 i 的总论文数。当我们找到一个 H 指数时跳出循环，并返回结果。

注意：官方给出的counter是使用vector数组的形式声明，vectorcounter(n+1)

但是我在实现的时候，使用的是int counter[n+1],所以必须注意此时需要将counter数组初始化。

class Solution {
public:int hIndex(vector<int>& citations) {int n = citations.size(), tot = 0;int counter[n+1];fill(counter,counter+n+1,0);for (int i = 0; i < n; i++) {if (citations[i] >= n) {counter[n]++;} else {counter[citations[i]]++;}}for (int i = n; i >= 1; i--) {tot += counter[i];if (tot >= i) {return i;}}return 0;}
};

时间复杂度：O（n）其中 n 为数组citations 的长度。需要遍历数组

空间复杂度：O（n）其中 nn 为数组citations 的长度。需要创建长度为n+1 的数组counter。

11. 453 最小操作次数使得数组元素相等

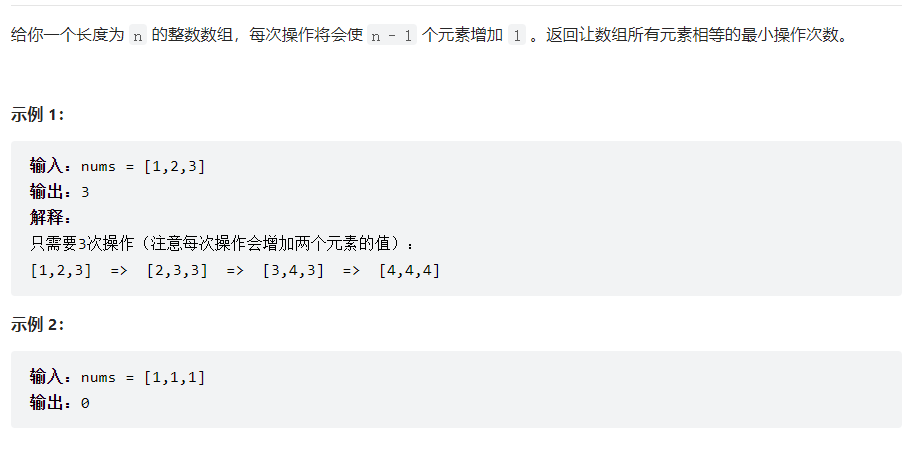
解法：这题找对思路很重要，一开始以为是动态规划类型得题，结果发现找不到状态转换方程。原来是一项逆向思维题。总体分两步骤：求最小值；求和

重点：因为题目只要求操作操作的次数，使得n-1个数字加1的操作其实等同于是得1个数字减一。

最后要求所有的数字都相同的最少操作，那么就让其余所有的数字向最小的那个数字看齐，也就是通过减一操作使得所有数字变成最小数的过程。

一个数字变成最小数字的操作：nums[i]-min。对所有的数字进行计算nums[i]-1,并且求和

代码：

class solution_10 {
public:int minMoves(vector<int>& nums) {int min=INT_MAX;//找到最小值for(int i=0;i<nums.size();i++){if (nums[i]<min){min=nums[i];}}//每个值和最小值之间的差别int res=0;for(int i=0;i<nums.size();i++){res+=nums[i]-min;}return res;}
};

时间复杂度：O（n）

空间复杂度: O（1）

12. 665 非递减数列

解法思路：一开始以为只要判断下降序列的次数，如果超过1就返回false，否则返回true。提交发现有问题，在[3,4,2,3]这个例子上面出错了，此时下降序列只有1，但是返回false。因此想到了下降序列的两个点，可能还和之前的点和之后的点构成的序列有关系。

如：【3，4，2，3】的例子，i=4时，出现nums[i]>nums[i+1],如果将4修改为2，那么[3,2,2,3]仍然不符合非递减。

所以此时要将nums[i]改为nums[i+1]明显是有条件的，必须nums[i-1]<=nums[i+1]

如果将2修改为4，序列[3,4,4,2]仍然不满足条件，因为此时4>2

所以此时要将nums[i+1]改为nums[i]明显是有条件的，必须nums[i]<=nums[i+2]

那么如果以上两种条件不满足的话，一定返回的false。即当i-1>=0且i+2<=nums.size()-1的时候，

num[i-1]>nums[i+1]&&nums[i]>nums[i+2]一定无法满足条件，因为满足了一边就无法满足另一半边了。

代码：

class solution_11 {
public:bool checkPossibility(vector<int>& nums) {int count=0;for(int i=0;i<nums.size()-1;i++){if(nums[i]>nums[i+1]){count++;}if(count>1){return false;}if((i>0&&nums[i-1]>nums[i+1])&&(i+1<nums.size()-1&&nums[i]>nums[i+2])){return false;}}return true;}
};

时间复杂度：O（n）

空间复杂度：O（1）

13. 283 移动零

解法：双指针

设置一个left指针和一个right指针，left指针和right指针，left和right的都赋值为0。left指针指向第一个为0的位置，right表示left后面第一个不为0的数字的位置。因此right指针为快指针，只需要判断right<nums.size为终止条件。因此当数字中不为0时，right和left同时移动，当找到第一个为0的left指针位置时候，此时right指针也指向left指针。此时需要找到第一个不为0的位置，也就是right指针位置。如果找到不为0的位置，那么将left和right位置的数转换。

举例:

12 3 0 1 0 2

left=2 right=3 ->swap(nums[2],nums[3]) 12 3 1 0 0 2

left =3 right=4

left=3 right=5 swap(nums[3],nums[5]) 12 3 1 2 0 0

right=6 退出循环

代码：

class Solution_12 {
public:void moveZeroes(vector<int>& nums) {if(nums.size()==1){return;}int left=0,right=0;while(right<nums.size()){if(nums[left]==0){while(right<nums.size()&&nums[right]==0){right++;}if(right<nums.size())swap(nums[left],nums[right]);}left++;right++;}for(int n:nums){cout<<n<<" ";}}void swap(int &a,int &b){int tmp=a;a=b;b=tmp;}
};

时间复杂度：O（n）

空间复杂度：O（1）

14. 118 杨辉三角

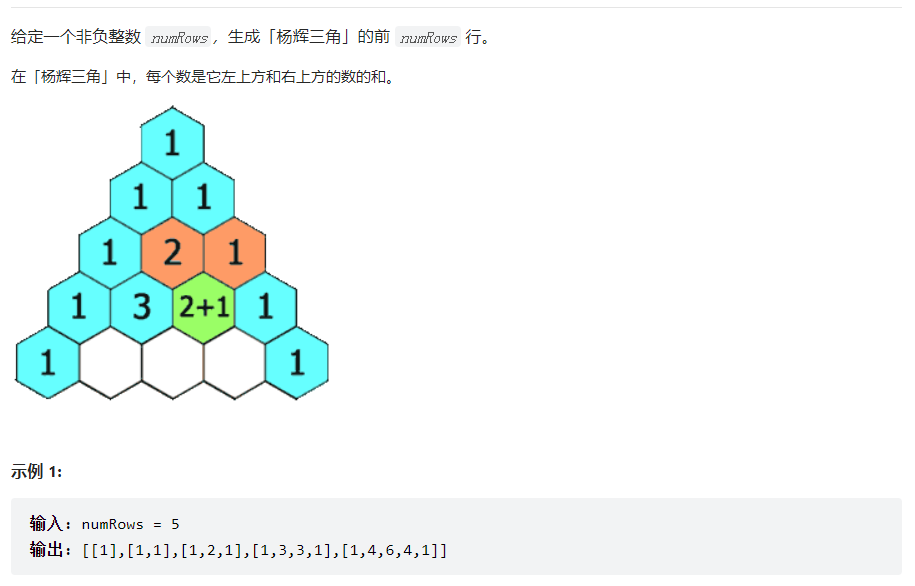
解法：杨辉三角，除了第一行外，每一行的第一个数以及最后一个数都为1，其他的为上一行的该位置以及下一个位置之和。因此可以进行双重循环 $res u lt [j] [i] == res u lt [j - 1] [i - 1] + res u lt [j] [i] ∣∣ res u lt [j] [i] == 0 （第一个或者最后一个数字）$

注意：vector中需要使用resize定义vector数组的大小，否则不能进行随机访问

代码：

class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>>result(numRows);result[0].push_back(1);for(int j=1;j<numRows;j++){result[j].resize(j+1);for(int i=0;i<=j;i++){if(i==0||i==j){result[j][i]=1;}else{result[j][i]=result[j-1][i]+result[j-1][i-1];}}}return result;}
};

时间复杂度：O（n^2）

空间复杂度：O（1）

15. 119 杨辉三角II

解法：可以像118题目一样从1已知列举到目标行，但是空间复杂度就高了。而根据杨辉三角的更新规律，可以使用动态规划的思想，只在这一行进行改变。

假设结果集合为res[rowIndex+1],除了第一个和最后一个数字为1外，其余位置的更新等于前一行的此位置和前一个位置之和，所以状态转移方程为 $res [j] = res [j] + res [j - 1]$ (j>0且j!=最后一位)

初始化时res[0]=1

若rowIndex=3

举例说明：

初始{1}

第1位为1{1，1}

第2位为1{1，1，1}

根据状态转移方程更新第1位置，res[1]=res[1]+res[0]=1+1=2 {1,2,1}

第3位为1{1，2，1，1}

根据状态转移方程跟新第2和第1位置，注意从后往前更新，否则覆盖答案。

更新第2位置：{1，2，3，1}

更新第1位置：{1，3，3，1}

因此更新的位置是除了第一个位置和最后一个位置的其他位置

代码：

class solution_14 {
public:vector<int> getRow(int rowIndex) {vector<int>result(rowIndex+1);result[0]=1;for(int i=1;i<=rowIndex;i++){result[i]=1;for(int j=i-1;j>0;j--){result[j]=result[j]+result[j-1];}}return result;}
};

时间复杂度：O（n^2）

空间复杂度：O（1）

16. 661 图片平滑器

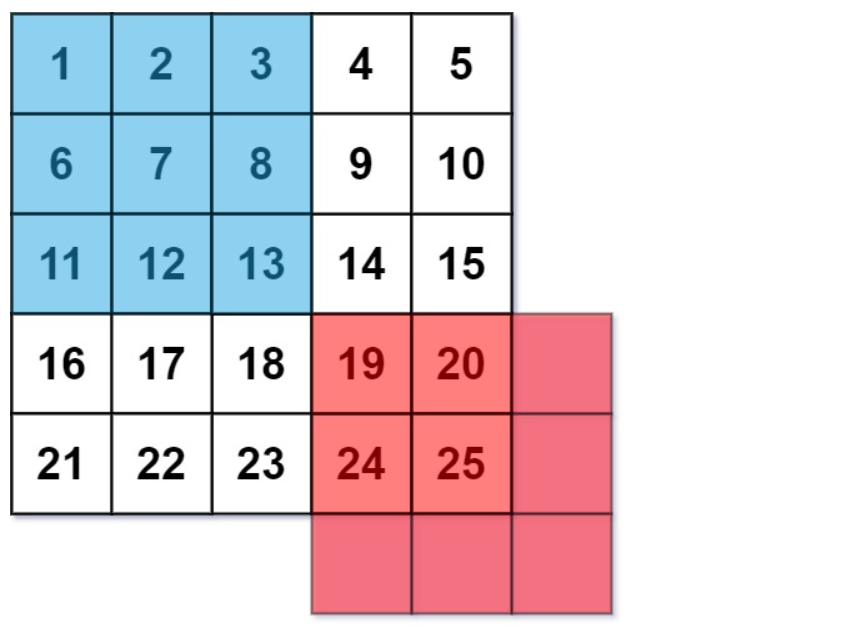
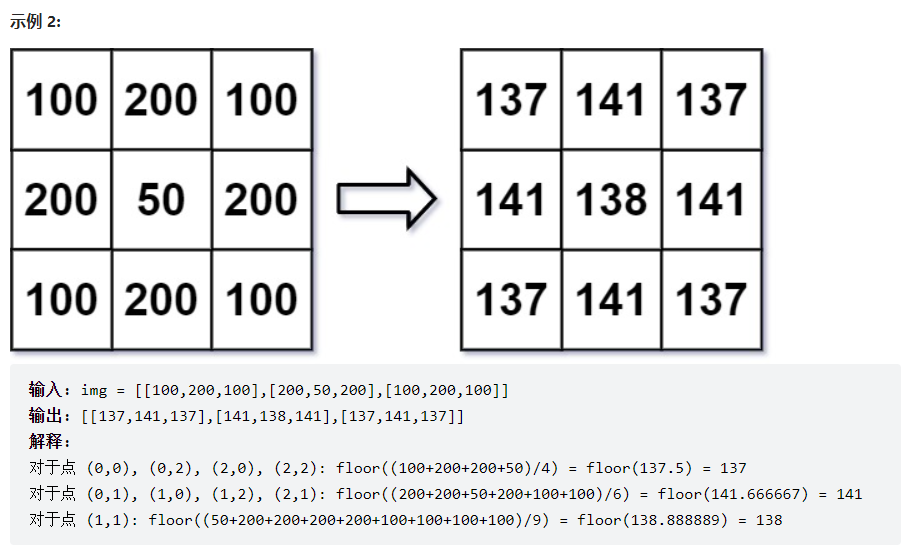
解法：

对于矩阵中的每一个单元格，只要找到9个包括它自身在内的紧邻的格子里的数组，将其相加取平困即可。然后取得的结果向下取整保存在和矩阵相同的二维数组中即可。

假设一个矩阵的节点为（x,y）则以它为中心的9个节点为

(x-1,y-1)	(x-1,y)	(x-1,y+1)
(x,y-1)	(x,y)	(x,y+1)
(x+1,y-1)	(x+1,y)	(x+1,y+1)

同时需要判断这九个节点是否都在这个矩阵的范围内，如果是则count技术加1，这九个节点的和都相加保存导result二维数组中。

代码：

class solution_15 {vector<vector<int>> imageSmoother(vector<vector<int>>& img) {int x=img.size();int y=img[0].size();vector<vector<int>>result(x,vector<int>(y,0));int count;for(int i=0;i<x;i++){for(int j=0;j<y;j++){count=0;for(int nx=i-1;nx<=i+1;nx++){for(int ny=j-1;ny<=j+1;ny++){if(nx>=0&&nx<x&&ny>=0&&ny<y){result[i][j]+=img[nx][ny];count++;}}}result[i][j]=result[i][j]/count;}}return result;}
};

17. 598 范围求和 II

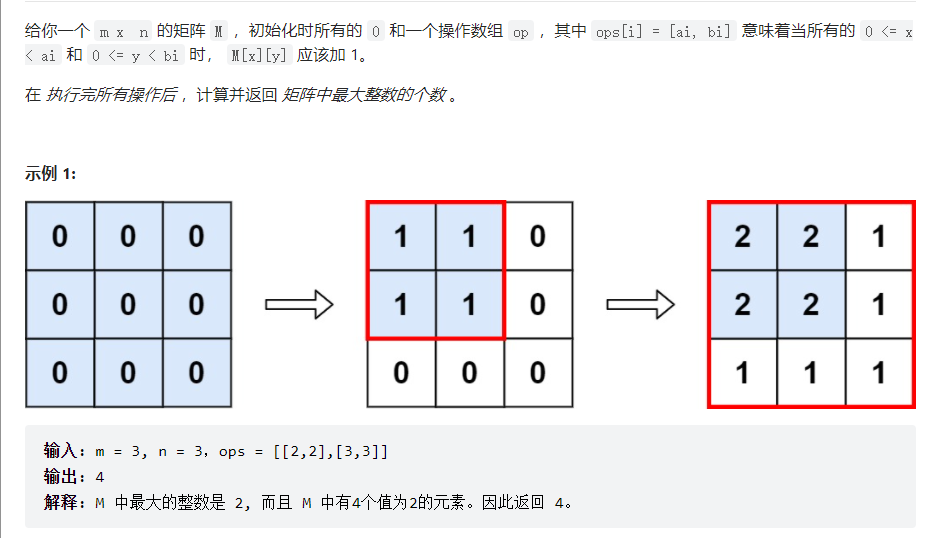
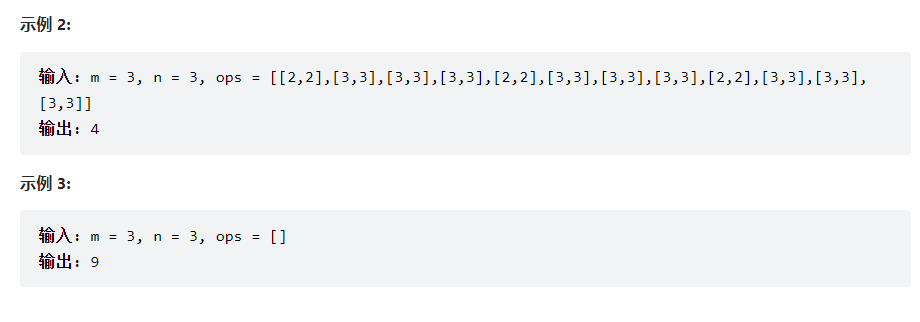
解法：

首先想到的是最常规的解法，将ops范围内的数加1，但是这种解法需要三重循环，时间复杂度为O（n^3）在数据大的时候超时。

正确的解法为，注意到题目中0<=x<ai,0<=y<bi,已知包含（0，0）点，所以每次操作都是在以（0，0）点为起点的矩形内数字加1。

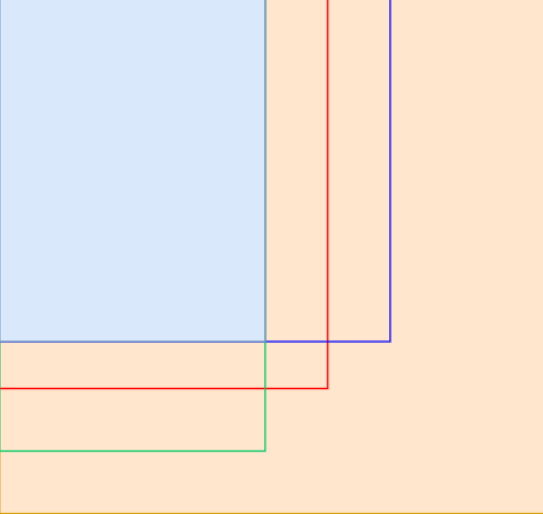
那么最大整数的个数，就是这些矩形中的长宽都最小的矩形大小。即找到最小的长宽即可。

代码：

class solution_16 {
public://常规解法 超时int maxCount(int m, int n, vector<vector<int>>& ops) {vector<vector<int>> result(m, vector<int>(n, 0));for (int i = 0; i < ops.size(); i++) {int nx = ops[i][0];int ny = ops[i][1];for (int m = 0; m < nx; m++) {for (int n = 0; n < ny; n++) {result[m][n]= result[m][n]+1;}}}int max = 0;int count = 0;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++) {if (result[i][j] == max) {count++;}if (result[i][j] > max) {max = result[i][j];count = 1;}}return count;}//正确解法 数学解法int maxCount2(int m, int n, vector<vector<int>>& ops) {int minx=m;int miny=n;for(int i=0;i<ops.size();i++){int x=ops[i][0];int y=ops[i][1];minx=min(minx,x);miny=min(miny,y);}return minx*miny;}
};

时间复杂度：O(k)，其中 k是数组ops 的长度。

空间复杂度：O(1)

18. 419 甲板上的战舰

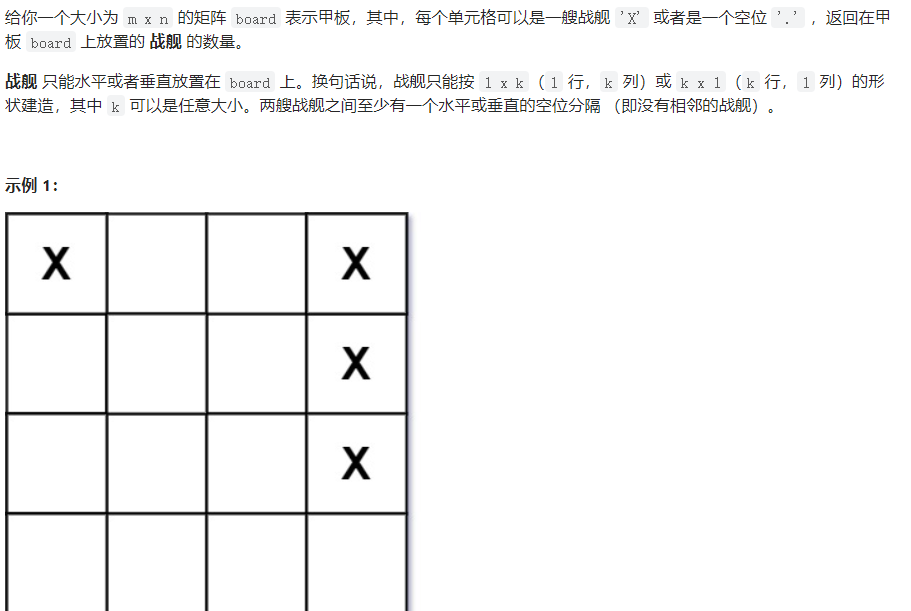
解法：这题首先是理解题目的意思，题目的意思其实是，这个战舰可以是连续的竖着一列X，也可以是连续横着的一行X，有连续X组成的战舰之间必须有分割。例如，

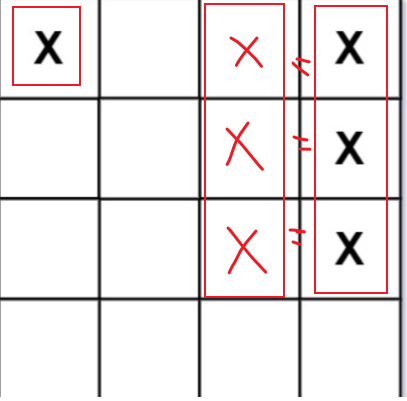
在上述的例子中，共有两个战舰，因为竖着的两个战舰之间无间隔，所以只能算一个战舰。

遍历计算战舰的方法有两种，可以遍历矩阵，将以X为起点的战舰位置都设置为空位，即X开始同行和同列的X都设置为空位。统计仍存在的X的个数，就是战舰个数。

这里用第二种方法实现，不需要改变原有的矩阵，就是计算每个战舰队列的战舰头的位置即可。因为战舰之间必须有水平或者垂直的间隔。如果一个战舰的左侧和上方都是空位或者围墙，那么战舰的个数加1。统计符合条件的顶点数，就是所有战舰的个数了。

即 $b or a d [i] [j] = =^{'} X^{'}$

$b or a d [i] [j - 1] = =^{'} .^{'}$

$b or a d [i - 1] [j] = =^{'} .^{'}$

满足此条件即为一条战舰。

代码：

class solution_17 {
public:int countBattleships(vector<vector<char>>& board) {int row=board.size();int col= board[0].size();int cnt=0;for(int i=0;i<row;i++){for(int j=0;j<col;j++){if(board[i][j]=='X'){if(i>0&&board[i-1][j]=='X'){continue;}if(j>0&&board[i][j-1]=='X'){continue;}cnt++;}}}return cnt;}
};

时间复杂度：O(m×n)，其中 m 是矩阵的行数，n 是矩阵的列数，我们只需要遍历一遍矩阵中每个位置即可。

空间复杂度：O(1)

19. 189 轮转数组

解法：最开始解法使用就地移位的方式，n=数组的长度，那么每次都将前n-1个数字后移，然后将最后一个放到第一个位置。即按照题目的要去每次翻转一次。但是这种方式在37个案例的时候超时。

解法二：就地翻转。题目的意思就是将后k个数组移动到前k个上。

以例1为例：[1,2,3,4,5,6,7]

首先可以将整个数组翻转=>[7,6,5,4,3,2,1]

然后将前k个数字翻转：[5,6,7,4,3,2,1]

再将后n-k个数字翻转：[5,6,7,1,2,3,4]

class solution_18 {
public://打算向后移动位数的方法 超时void rotate2(vector<int>& nums, int k) {int temp;int n=nums.size()-1;while(k){temp=nums[n];for(int i=n-1;i>=0;i--){nums[i+1]=nums[i];}nums[0]=temp;k--;}
//        for(int num:nums){
//            cout<<num<<" ";
//        }}//前后翻转 可用void rotate(vector<int>& nums, int k) {int n=nums.size()-1;k=k%nums.size();reverse(nums,0,n);reverse(nums,0,k-1);reverse(nums,k,n);}void reverse(vector<int>&nums,int start,int end){while(start<end){int temp=nums[end];nums[end]=nums[start];nums[start]=temp;start+=1;end-=1;}}
};

时间复杂度：O(n)，其中 n 为数组的长度。每个元素被翻转两次，一共 n 个元素，因此总时间复杂度为 O(2n)=O(n)。

空间复杂度：O(1)

20. 396 旋转函数

解法：利用类似等差数列解法，采用动态规划的思想求解。

动态规划的状态方程： $F （ k ） = F (k - 1) + s u m - n * n u m s [n - k]$

如何得到？

假设

$F (0) = 0 * a [0] + 1 * a [1] + 2 * a [2] + ... + (n - 1) * a [n - 1]$

$F (1) = 0 * a [n - 1] + 1 * a [0] + 2 * a [1] + ... + (n - 1) * a [n - 2]$

$F (2) = 0 * a [n - 2] + 1 * a [n - 1] + 2 * a [0] + ... + (n - 1) * a [n - 2]$

观察到F(0)、F(1)、F(2)的变化类似于等差数列的求和，当F（0）的所有位置都加上一个a[i]

会得到

$F (0)^{'} = 1 * a [0] + 2 * a [1] + 3 * a [2] + ... + (n - 1) * a [n - 2] + n * a [n - 1]$

$F(1)-F(0)^‘=0*a[n-1]-n*a[n-1] 即F(1)=F(0)'-n*a[n-1]$

同理得到 $F(2)-F(1)^‘=0*a[n-2]-n*a[n-2] 即F(2)=F(1)'-n*a[n-2]$

所以假设$sum=nums[0]+nums[1]+…+nums[n-1] $

$所以F(k)^‘=F(k-1)+sum$

所以状态转移方程为 $F （ k ） = F (k - 1) + s u m - n * n u m s [n - k]$

每次求得F（k）之后取最大值即可，因为题目保证让测试案例不超过32位，即没有超过int的范围。直接使用int即可。

class solution_19 {
public:int maxRotateFunction(vector<int>& nums) {int f0=0;int sum=0;int n=nums.size();for(int i=0;i<n;i++){f0+=i*nums[i];sum+=nums[i];}int m=f0;for(int i=1;i<n;i++){f0=f0+sum-n*nums[n-i];m=max(m,f0);}return m;}
};

时间复杂度：O(n)，其中 n是数组 }nums 的长度。计算 Sum 和第一个 f 消耗 O(n) 时间，后续迭代n−1 次 f 消耗 O(n)时间。

空间复杂度：O(1)。仅使用常数空间。

21. 54 螺旋矩阵

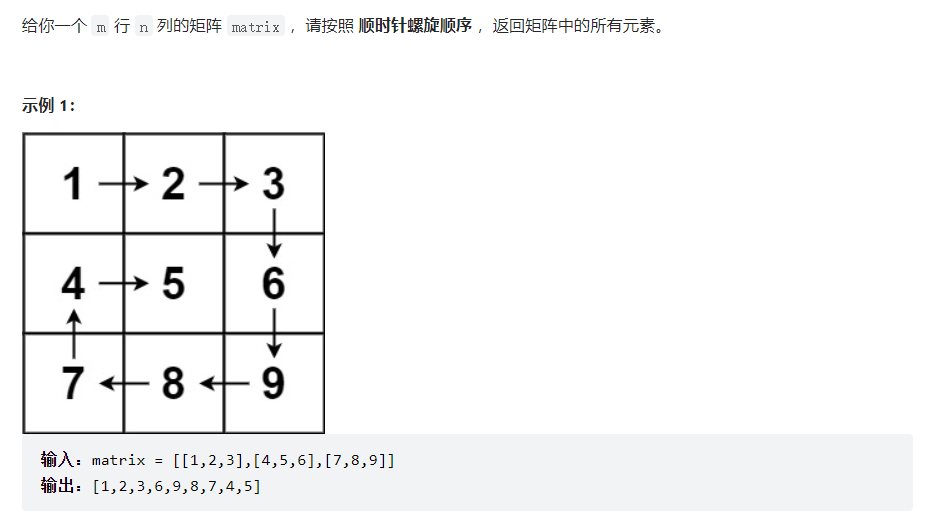
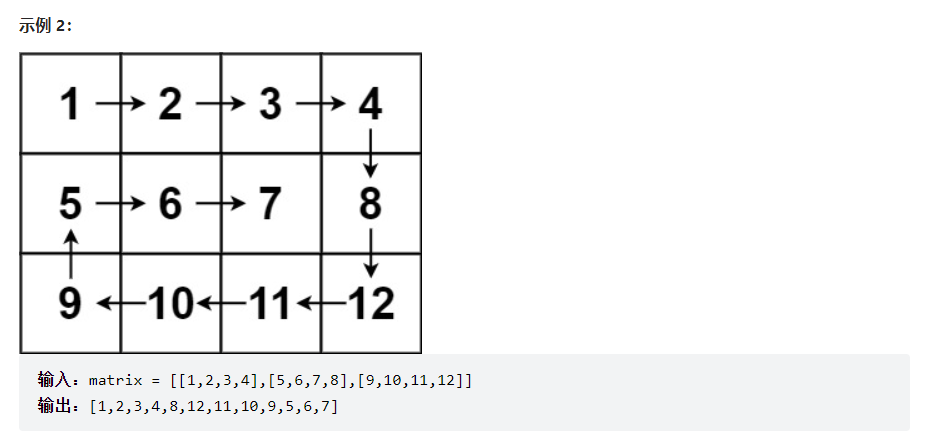
解法：因为观察到顺时针方向是按照右、下、左、上的顺序执行的，因此可以用递归的方式按照此顺序遍历矩阵，只有在遍历位置超出矩阵长度范围，或者此节点已经访问过，才会改变下一个方向。

因此设置direction数组，表示右、下、左、上四个方向。status表示此次取到的direction的方向索引，可例2可以看到，当5遍历到1时，发现已经访问呢，因此会转向右方向，因此可以用取余的方式遇到阻碍需要转向。

需要注意dfs递归的终点是当result的结果等于矩阵的大小，说明已经遍历结束，可以返回。

代码：

const int direction[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
class solution_20 {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {vector<int>result;vector<vector<int>>flag(matrix.size(),vector<int>(matrix[0].size(),0));int status=0;dfs(matrix,flag,result,0,0,status);for(int num:result){cout<<num<<" ";}return result;}void dfs(vector<vector<int>>&matrix,vector<vector<int>>&flag,vector<int> &result,int i,int j,int status){flag[i][j]=1;result.push_back(matrix[i][j]);if(result.size()==matrix.size()*matrix[0].size()){return ;}int nextI=i+direction[status][0];int nextJ=j+direction[status][1];if(nextI<0||nextI>=matrix.size()||nextJ<0||nextJ>=matrix[0].size()||flag[nextI][nextJ]==1){status=(status+1)%4;}dfs(matrix,flag,result,i+direction[status][0],j+direction[status][1],status);}
};

时间复杂度：O(mn)，其中 m 和 n 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。

空间复杂度：O(mn)。需要创建一个大小为 m×n 的矩阵 visited 记录每个位置是否被访问过。

22. 59 螺旋矩阵II

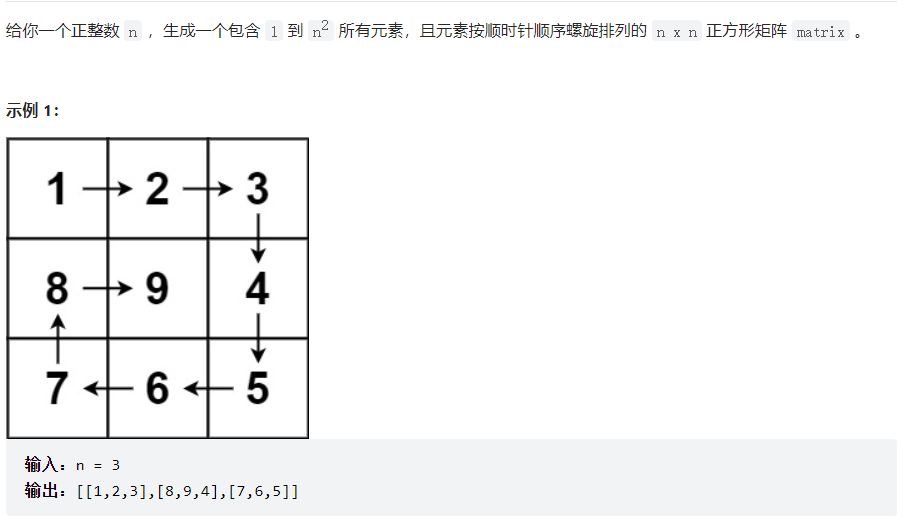
解法：可以采用和54相似的思路，按照右下左上的顺序，将1-n^2的数字依次填充到矩阵中，用一个二维数组matrix保存最后结果，初始化全为0，如果碰到越界或者该位置数字已经不为0，就转变方向，继续递归。直到所有的元素都已经在矩阵中了，即cnt=n*n了返回。

const int direction[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
class solution_21 {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>>matrix(n,vector<int>(n,0));int cnt=0;int status=0;dfs(matrix,n,cnt,0,0,status);for(int i=0;i<n;i++){for(int j=0;j<n;j++){cout<<matrix[i][j]<<" ";}cout<<endl;}}void dfs(vector<vector<int>>&matrix,int n,int cnt,int i,int j,int status){cnt++;matrix[i][j]=cnt;if(cnt==n*n){return;}int nextI=i+direction[status][0];int nextJ=j+direction[status][1];if(nextI<0||nextI>=matrix.size()||nextJ<0||nextJ>=matrix[0].size()||matrix[nextI][nextJ]!=0){status=(status+1)%4;}dfs(matrix,n,cnt,i+direction[status][0],j+direction[status][1],status);}
};

时间复杂度：O(mn)，其中 m 和 n 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。

空间复杂度：O(mn)。需要创建一个大小为 m×n 的矩阵 visited 记录每个位置是否被访问过。

23. 498 对角线遍历

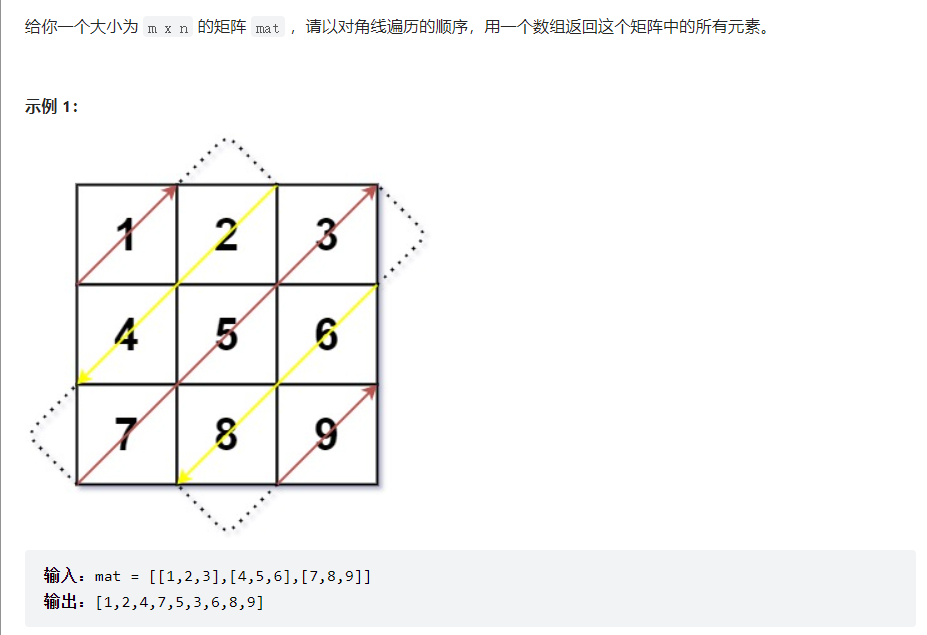
解法：简单模拟遍历，可以看到按照对角线遍历的规律，若从左下角到右上角，则x-1,y+1;

若从右上角到左下角，则x+1,y-1;

flag=0,表示从左下到右上；flag=1表示右下到左上。

访问对角线需要转方向的时候：若左下到右上越界，则转变方向向右，x不变，y+1,此时需要注意，当位于3这个点时候，若转向向右，则为（0，3）点不正确，应为（1，2）点，因此若y+1>mat[0].size的话，y不变，x+1。

同理当从右上到左下时候，位于7的点，x+1>mat.size时候，x不变，y+1

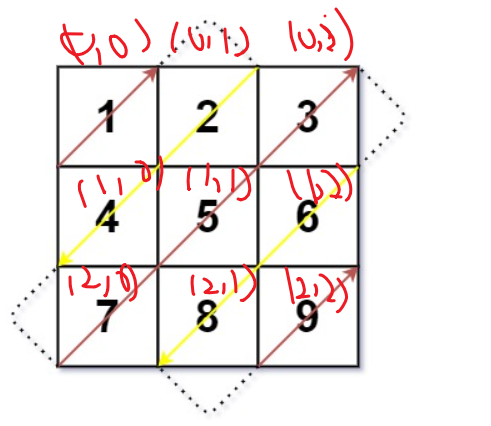
代码：

class solution_22 {
public:vector<int>result;vector<int> findDiagonalOrder(vector<vector<int>>& mat) {int x,y,nx,ny;int flag=0;x=0;y=0;int row=mat.size();int col=mat[0].size();while(result.size()!=mat.size()*mat[0].size()){result.push_back(mat[x][y]);nx=x+direction[flag][0];ny=y+direction[flag][1];if(nx>=row||nx<0||ny>=col||ny<0){if(flag==0){//如果flag=0是向右移动，但是同时注意若移动到最右边即y+1>=m，应该向下移动nx=y+1<mat[0].size()?x:x+1;ny=y+1<mat[0].size()?y+1:y;}else{//如果flag=1是向下移动，但是同时注意若移动到最下边即x+1>=m，应该向右移动nx=x+1<mat.size()?x+1:x;ny=x+1<mat.size()?y:y+1;}flag=(flag+1)%2;}x=nx;y=ny;}return result;}};

时间复杂度：O（n*m）

空间复杂度：O（1）

24. 566 重塑矩阵

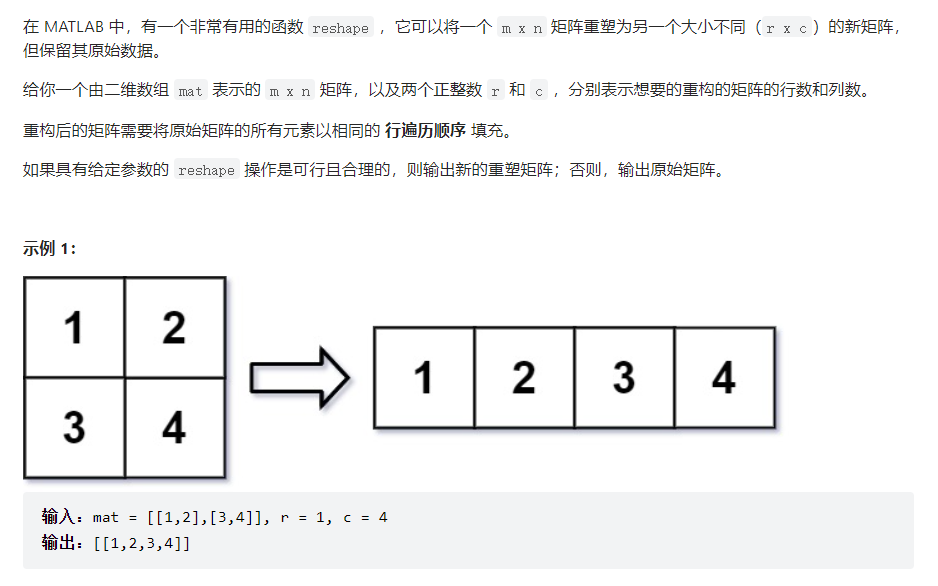
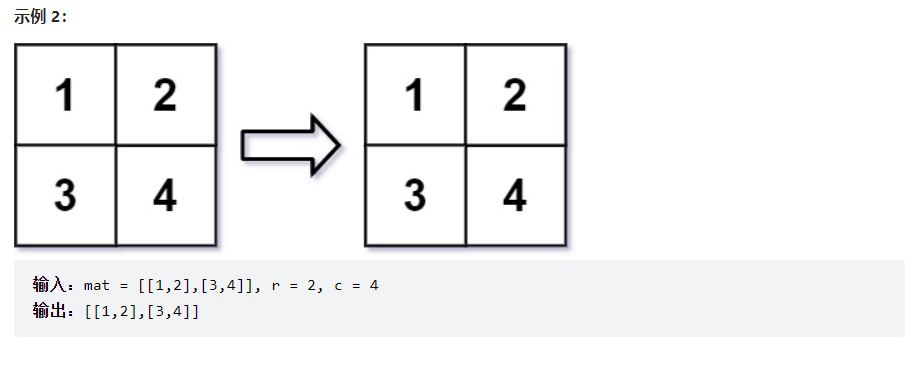
解法：

对于一个行数为 m，列数为 n，行列下标都从 0 开始编号的二维数组，将其中的每个元素 (i,j) 映射到整数域内，并且它们按照行优先的顺序一一对应着 [0,mn) 中的每一个整数。形象化地来说，我们把这个二维数组变成了一个一维数组。

映射为 $(i, j) - > i * n + j$

同样的可以将一个整数x映射到矩阵的下标：

i=x/n, j=x%n

所以此题需要两步骤：

将二位数组nums映射成一维数组
将一维数组映射回r行c列的二维数组

代码：

class solution_23 {
public:vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {vector<vector<int>>result(r,vector<int>(c,0));int row=mat.size();int col=mat[0].size();if((row*col)!=(r*c)){return mat;}for(int i=0;i<row*col;i++){result[i/c][i%c]=mat[i/col][i%col];}return result;}
};

时间复杂度：O(rc)。这里的时间复杂度是在重塑矩阵成功的前提下的时间复杂度，否则当 mn =rc 时，C++ 语言中返回的是原数组的一份拷贝，本质上需要的时间复杂度为 O(mn)，而其余语言可以直接返回原数组的对象，需要的时间复杂度仅为 O(1)。

空间复杂度：O(1)。这里的空间复杂度不包含返回的重塑矩阵需要的空间

25. 73 矩阵置零

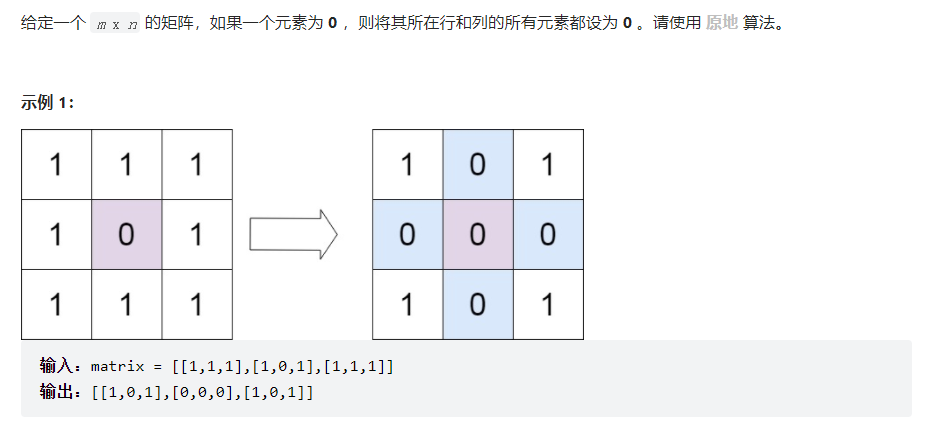
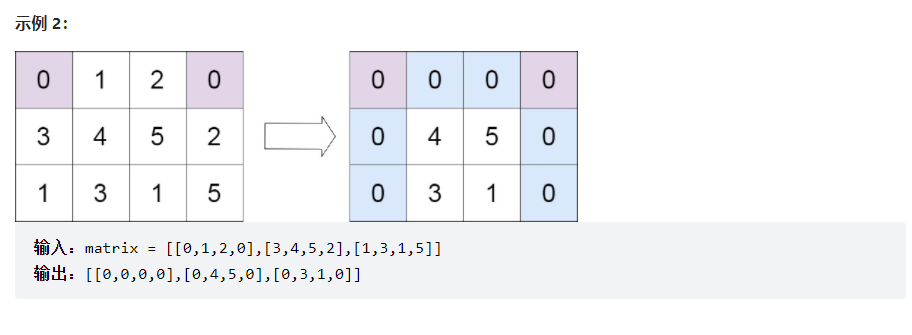
解法：简单标记，循环遍历矩阵，将矩阵为0的位置的行和列记录下来，放入set集合中去重，然后

再次遍历矩阵，若这个位置的行或者列在set集合中，那么就将这个位置置为1。

代码：

class solution_24 {
public:void setZeroes(vector<vector<int>>& matrix) {set<int>row;set<int>col;for(int i=0;i<matrix.size();i++)for(int j=0;j<matrix[0].size();j++){if(matrix[i][j]==0) {row.insert(i);col.insert(j);}}for(int i=0;i<matrix.size();i++)for(int j=0;j<matrix[0].size();j++){if(row.count(i)==1||col.count(j)==1){matrix[i][j]=0;}}}
};

时间复杂度：O(mn)，其中 m是矩阵的行数，n 是矩阵的列数。我们至多只需要遍历该矩阵两次。

空间复杂度：O(m+n)，其中 m 是矩阵的行数，n 是矩阵的列数。我们需要分别记录每一行或每一列是否有零出现。

26.289 生命游戏

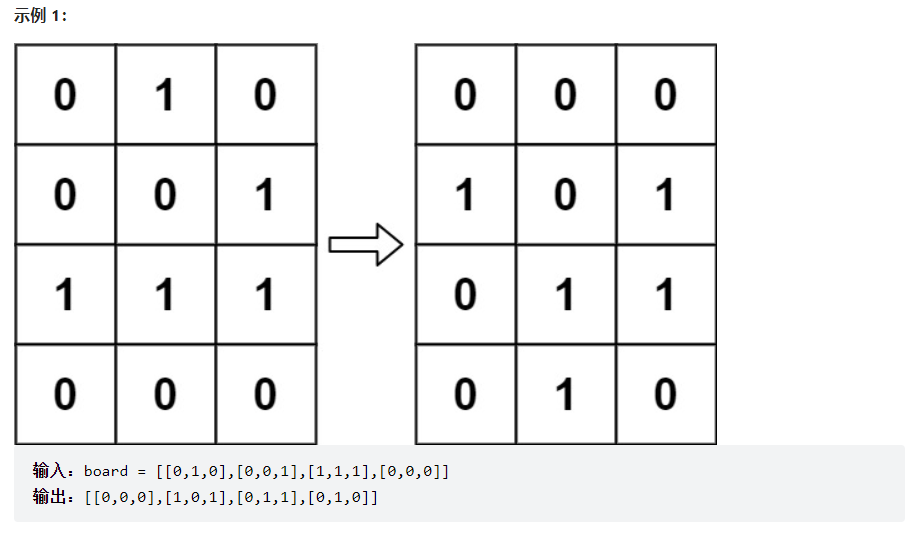
解法：

注意到不能根据每个细胞位置的八个方向的活细胞或者死细胞数字更新数组，这样无法做到题目中的同步更新。因为下一状态是根据当前状态生成的，如果更新后，后面的位置的细胞状态可能收到最新更新的细胞状态的影响。因此，我的解法是遍历这个board数组，对于每个位置的八个方向的活细胞数字进行统计，然后将原来数组中需要翻转数字的位置索引记录下来。

如果是活细胞，并且活细胞的数目<2或者>3,那么该活细胞要变成死细胞，所以该位置需要翻转，记录结果。

如果是死细胞，并且活细胞的数组=3，死细胞变为活细胞，也需要翻转

对于如果是活细胞，并且周围活细胞数组=2或者=2，仍然是活细胞，不需要翻转，即不需要记录。

最后遍历一次board，将索引的位置进行翻转。

class solution_25 {
public:int direction[8][2]={{-1,0},{1,0},{0,-1},{0,1},{-1,-1},{1,1},{-1,1},{1,-1}};void gameOfLife(vector<vector<int>>& board) {vector<pair<int,int>>result;int count=0;int x,y,nx,ny;for(int i=0;i<board.size();i++){for(int j=0;j<board[0].size();j++){count=0;x=i;y=j;for(int k=0;k<8;k++){nx=i+direction[k][0];ny=j+direction[k][1];if(nx>=0&&nx<board.size()&&ny>=0&&ny<board[0].size()){if(board[nx][ny]){count++;}}}if(board[x][y]==1){if(count<2||count>3){result.push_back(make_pair(x,y));}}if(board[x][y]==0&&count==3){result.push_back(make_pair(x,y));}}}//遍历修改for(int i=0;i<board.size();i++){for(int j=0;j<board[0].size();j++){if(find(result.begin(),result.end(), make_pair(i,j))!=result.end()){if(board[i][j]==0){board[i][j]=1;}else{board[i][j]=0;}cout<<board[i][j];}}}}
};

时间复杂度：O（mn）

空间复杂度：O（mn）

27. 303 区域和检索–数组不可变

解法一：暴力解法

从left到right进行求和操作

class NumArray {
public:vector<int>n;NumArray(vector<int>& nums) {this->n.assign(nums.begin(),nums.end());}int sumRange(int left, int right) {int sum=0;for(int i=left;i<=right;i++){sum+=n[i];}return sum;}
};

时间复杂度：O（n^2）

空间复杂度：O（n）

解法二：预处理得到前缀和。sumsRange(left,right)其实可以用nums[0,right]的和-nums[0,left-1]。

所以只需要记录到每个位置的前缀和即可，但是left-1有可能越界，如果将sums数组的大小定位nums.size()+1。

sums[i+1]=nums[i]+sums[i]; 所以sums[i]表示的是从nums[0，i-1]的所有的数字和

即sumsRange[left,right]=sums[right+1]-sums[left]

代码：

class NumArray {
public:vector<int>sums;NumArray(vector<int>& nums) {sums.resize(nums.size()+1);for(int i=0;i<nums.size();i++){sums[i+1]=sums[i]+nums[i];}}int sumRange(int left, int right) {return sums[right+1]-sums[left];}
};/*** Your NumArray object will be instantiated and called as such:* NumArray* obj = new NumArray(nums);* int param_1 = obj->sumRange(left,right);*/

时间复杂度：初始化 O(n)，每次检索 O(1)，其中 n 是数组 nums 的长度。初始化需要遍历数组 nums 计算前缀和，时间复杂度是 O(n)。每次检索只需要得到两个下标处的前缀和，然后计算差值，时间复杂度是 O(1)。

空间复杂度：O(n)，其中 n是数组 nums 的长度。需要创建一个长度为n+1 的前缀和数组。

28. 304 二维区域和检索-矩阵不可变

解法：二维数组前缀和，关于二维数组前缀和的算法见

二维数组前缀和

代码：

class NumMatrix {
public:    vector<vector<int>>sums;NumMatrix(vector<vector<int>>& matrix) {int row=matrix.size();int col=matrix[0].size();sums.resize(row+1,vector<int>(col+1,0));//预处理for(int i=1;i<=row;i++)for(int j=1;j<=col;j++){sums[i][j]=sums[i-1][j]+sums[i][j-1]-sums[i-1][j-1]+matrix[i-1][j-1];}}int sumRegion(int row1, int col1, int row2, int col2) {row1+=1;col1+=1;row2+=1;col2+=1;return sums[row2][col2]-sums[row1-1][col2]-sums[row2][col1-1]+sums[row1-1][col1-1];}
};

时间复杂度：初始化 O(mn)，每次检索O(1)，其中 m 和 n 分别是矩阵matrix 的行数和列数。
初始化需要遍历矩阵 matrix 计算二维前缀和，时间复杂度是O(mn)。
每次检索的时间复杂度是 O(1)。

空间复杂度：O(mn)，其中 m 和 n 分别是矩阵 matrix 的行数和列数。需要创建一个m+1 行 n+1 列的二维前缀和数组 sums。

29. 238 除自身以外数组的乘积

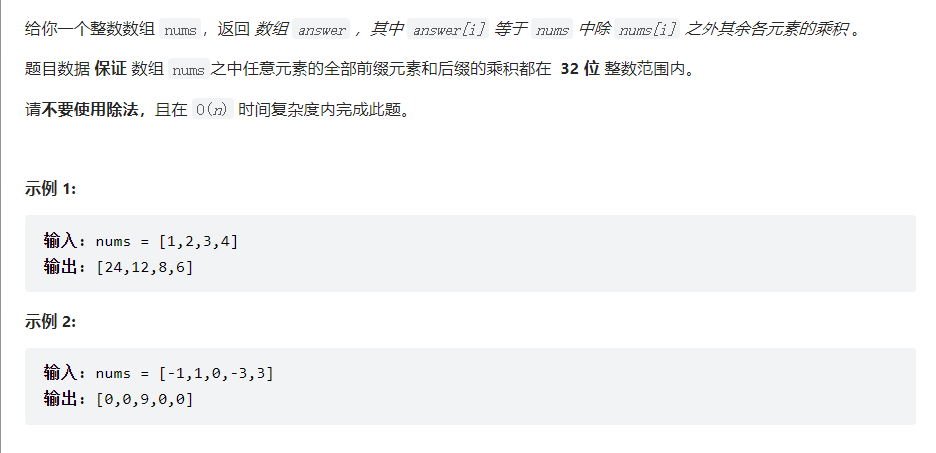
解法：注意题目要求不能使用除法，如果要求一个nums中除nums[i]之外的其余各元素的乘积。

一种方法是所有乘积除以nums[i]，因为题目要求不能使用除法，所以这种方法不行。

因此可以换一种方式：nums[i]的左侧的数字乘积乘以nums[i]右侧的数字乘积。

通过预处理的方式得到两个数组，分别表示索引i位置左侧的乘积和右侧的乘积。

初始化两个空数组 L 和 R。对于给定索引 i，L[i] 代表的是 i 左侧所有数字的乘积，R[i] 代表的是 i 右侧所有数字的乘积。
用两个循环来填充 L 和 R 数组的值。对于数组 L，L[0] 应该是 1，因为第一个元素的左边没有元素。对于其他元素：L[i] = L[i-1] * nums[i-1]。
同理，对于数组 R，R[nums.size()-1] 应为 1。length 指的是输入数组的大小。

其他元素：R[i] = R[i+1] * nums[i+1]。
当 R 和 L 数组填充完成，我们只需要在输入数组上迭代，且索引 i 处的值为：L[i] * R[i]。

代码：

class solution_28 {
public:vector<int> productExceptSelf(vector<int>& nums) {vector<int>result(nums.size());vector<int>left(nums.size(),0);vector<int>right(nums.size(),0);left[0]=1;//left[i]表示索引i左侧所有元素乘积for(int i=1;i<nums.size();i++){left[i]=left[i-1]*nums[i-1];}right[nums.size()-1]=1;//right[i]表示索引i右侧所有元素乘积for(int i=nums.size()-2;i>=0;i--){right[i]=right[i+1]*nums[i+1];}for(int i=0;i<nums.size();i++){result[i]=left[i]*right[i];}return result;}
};

时间复杂度：O(N)，其中 N 指的是数组 nums 的大小。预处理 L 和 R 数组以及最后的遍历计算都是 O(N) 的时间复杂度。

空间复杂度：O(N)，其中 N指的是数组 nums 的大小。使用了 L 和 R 数组去构造答案，L 和 R 数组的长度为数组 nums 的大小。