题目链接
Leetcode.174 地下城游戏
hard
题目描述
恶魔们抓住了公主并将她关在了地下城 d u n g e o n dungeon dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 0 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0 0 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
示例 1:
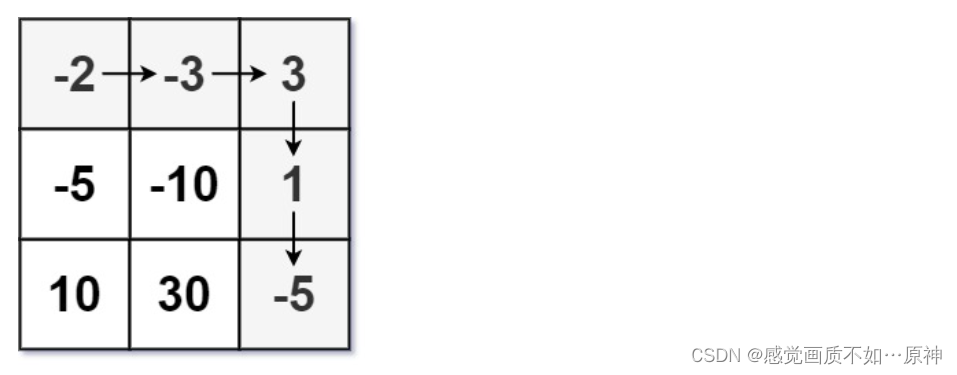
输入:dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出:7
解释:如果骑士遵循最佳路径:右 -> 右 -> 下 -> 下 ,则骑士的初始健康点数至少为 7 。
示例 2:
输入:dungeon = [[0]]
输出:1
提示:
- m = d u n g e o n . l e n g t h m = dungeon.length m=dungeon.length
- n = d u n g e o n [ i ] . l e n g t h n = dungeon[i].length n=dungeon[i].length
- 1 ≤ m , n ≤ 200 1 \leq m, n \leq 200 1≤m,n≤200
- − 1000 ≤ d u n g e o n [ i ] [ j ] ≤ 1000 -1000 \leq dungeon[i][j] \leq 1000 −1000≤dungeon[i][j]≤1000
解法:动态规划
假设我们考虑从左上角到右下角,这样的话我们需要考虑两个因素:当前路径和 ,当前路径上的最小路径和。因为存在两个同等重要的因素,所以我们无法确定下一个位置。
既然从左上角到右下角不行,那么我们就考虑从右下角到左上角。
考虑从右下角到左上角,我们定义 f ( i , j ) f(i,j) f(i,j) 为从位置 ( i , j ) (i,j) (i,j) 到终点 ( m − 1 , n − 1 ) (m-1,n-1) (m−1,n−1)所需要的最低初始健康点数。按照定义,最终我们返回的结果就是 f ( 0 , 0 ) f(0,0) f(0,0)。
f ( i , j ) f(i,j) f(i,j) 只与 f ( i + 1 , j ) f(i + 1,j) f(i+1,j) 和 f ( i , j + 1 ) f(i,j+1) f(i,j+1) 以及 d u n g e o n [ i ] [ j ] dungeon[i][j] dungeon[i][j] 有关。
即 f ( i , j ) = m i n { f [ i + 1 ] [ j ] , f [ i ] [ j + 1 ] } − d u n g e o n [ i ] [ j ] f(i,j) = min \{ f[i + 1][j] , f[i][j + 1] \} - dungeon[i][j] f(i,j)=min{f[i+1][j],f[i][j+1]}−dungeon[i][j]。
因为 f [ i ] [ j ] f[i][j] f[i][j] 必须是 ≥ 1 \geq1 ≥1 的,所以最终的转移方程为:
f ( i , j ) = m a x { m i n ( f [ i + 1 ] [ j ] , f [ i ] [ j + 1 ] ) − d u n g e o n [ i ] [ j ] , 1 } f(i,j) = max \{ min ( f[i + 1][j] , f[i][j + 1] ) - dungeon[i][j],1\} f(i,j)=max{min(f[i+1][j],f[i][j+1])−dungeon[i][j],1}
当 i = m − 1 i =m - 1 i=m−1 或者 j = n − 1 j = n- 1 j=n−1时, f [ i + 1 ] [ j ] f[i+1][j] f[i+1][j] 和 f [ i ] [ j + 1 ] f[i][j+1] f[i][j+1] 就会分别越界。初始直接定义 f [ i ] [ j ] f[i][j] f[i][j] 为一个较大的值,这里我设置的是 1 0 9 10^9 109。
特别需要注意的是,我们直接把 f [ m ] [ n − 1 ] f[m][n-1] f[m][n−1] 和 f [ m − 1 ] [ n ] f[m-1][n] f[m−1][n] 设置为 1 1 1,这样是为了让 f [ m − 1 ] [ n − 1 ] = d u n g e o n [ m − 1 ] [ n − 1 ] f[m-1][n-1] = dungeon[m-1][n-1] f[m−1][n−1]=dungeon[m−1][n−1]。
时间复杂度: O ( m × n ) O(m \times n) O(m×n)
C++代码:
class Solution {
public:int calculateMinimumHP(vector<vector<int>>& g) {int m = g.size() , n = g[0].size();vector<vector<int>> f(m + 1,vector<int>(n + 1,1e9));f[m][n - 1] = 1;f[m - 1][n] = 1;for(int i = m - 1;i >= 0;i--){for(int j = n - 1;j >= 0;j--){int t = min(f[i + 1][j],f[i][j + 1]);f[i][j] = max(t - g[i][j] , 1);}}return f[0][0];}
};