1.算法运行效果图预览

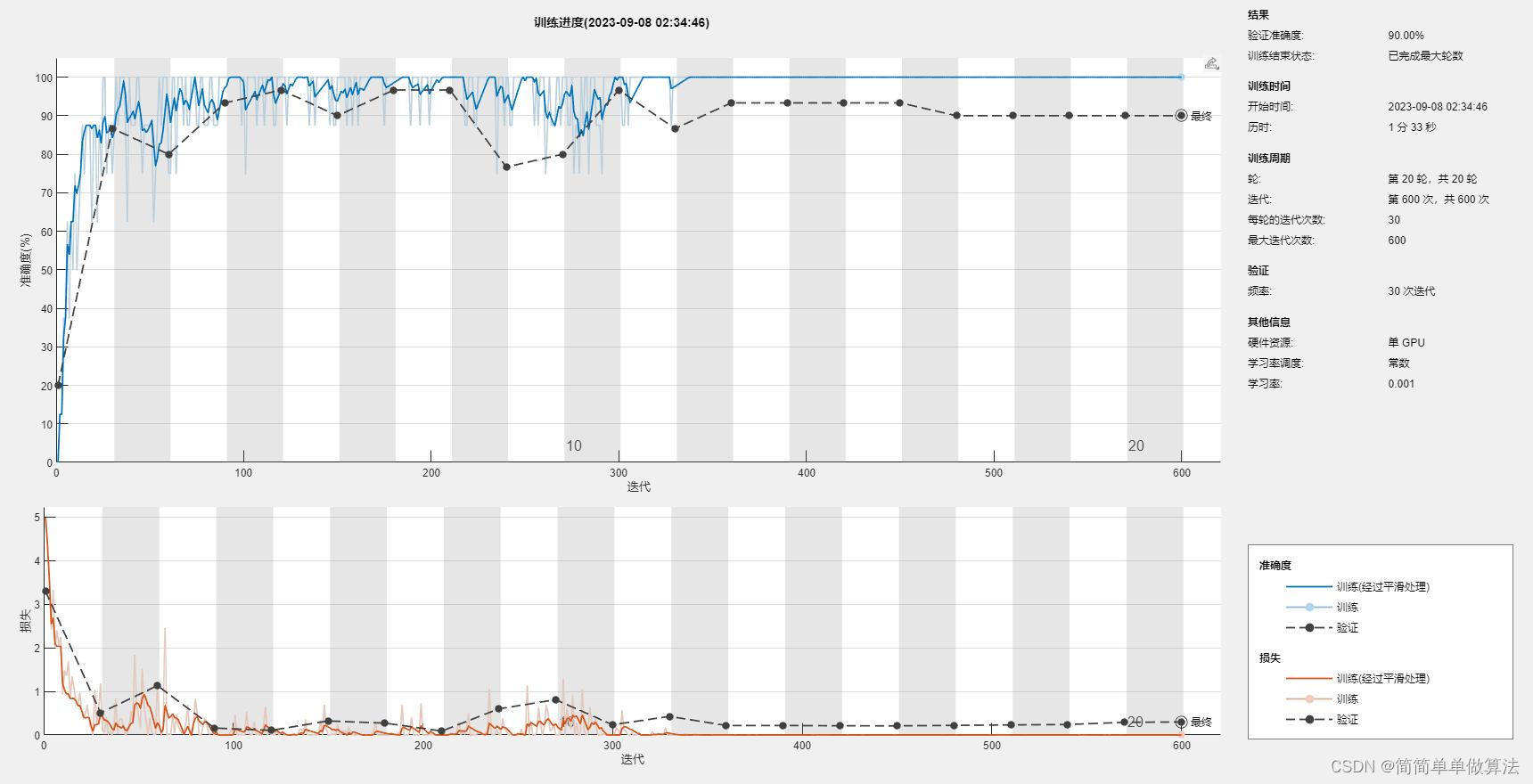
2.算法运行软件版本

matlab2022a

3.部分核心程序

.................................................................
% 获取输入层的尺寸
Input_Layer_Size = net.Layers(1).InputSize(1:2);% 调整训练、验证和测试数据集的图像尺寸Resized_Training_Dataset   = augmentedImageDatastore(Input_Layer_Size ,Training_Dataset);
Resized_Validation_Dataset = augmentedImageDatastore(Input_Layer_Size ,Validation_Dataset);
Resized_Testing_Dataset    = augmentedImageDatastore(Input_Layer_Size ,Testing_Dataset);% 设置训练参数
maxEpochs = 20;
Minibatch_Size = 8;
Validation_Frequency = floor(numel(Resized_Training_Dataset.Files)/Minibatch_Size);
Training_Options = trainingOptions('sgdm', ...'MiniBatchSize', Minibatch_Size, ...'MaxEpochs', maxEpochs, ...'InitialLearnRate', 1e-3, ...'Shuffle', 'every-epoch', ...'ValidationData', Resized_Validation_Dataset, ...'ValidationFrequency', Validation_Frequency, ...'Verbose', false, ...'Plots', 'training-progress');
% 使用训练数据训练新网络
net = trainNetwork(Resized_Training_Dataset, New_Network, Training_Options);save gnet.mat   
60

4.算法理论概述

动物种类识别算法基于深度学习技术，尤其是卷积神经网络（CNN），如GoogleNet。这种算法的主要原理是通过学习和识别图像中的特征来预测动物的种类。

GoogleNet，也被称为Inception v1，是在2014年由Google研发的深度学习模型。GoogleNet的特点是深度较大，增加了网络的复杂性，且引入了"Inception模块"，这个模块允许网络在同一层中处理不同大小的卷积核，从而能够捕捉到图像的不同尺度的特征。

基于GoogleNet的动物种类识别算法主要包括以下步骤：

数据预处理：首先，我们需要对图像进行预处理，包括调整大小，归一化像素值等。
构建GoogleNet模型：接下来，我们需要构建GoogleNet模型。GoogleNet模型由多个Inception模块和其他层组成。
训练模型：然后，我们用标注过的动物图像数据集来训练这个模型。这个过程中，模型会学习到如何识别动物的各种特征。
测试模型：最后，我们用一些没有在训练集中出现过的图像来测试模型的性能。

至于数学公式，卷积神经网络的主要运算包括卷积（Convolution），池化（Pooling），激活函数（Activation Function）等。这里涉及的公式比较复杂，我会尽量简化一下：

卷积：假设我们有一个输入图像X和一个卷积核K，那么卷积运算可以用以下公式表示：

s(t) = (X * K)(t) = ∫X(a)K(t - a)da

其中*代表卷积运算，t是一个二维坐标。

池化：池化操作一般使用最大池化（Max Pooling）或平均池化（Average Pooling）。以最大池化为例，假设我们有一个2x2的池化窗口，那么最大池化结果就是这个窗口中的最大值。
激活函数：激活函数有很多种，比如ReLU（Rectified Linear Unit），Sigmoid等。ReLU的函数形式可以表示为：

f(x) = max(0, x)

这只是卷积神经网络中的一部分数学原理。实际上，深度学习涉及到的数学和计算机科学知识非常广泛，包括线性代数，微积分，概率论，优化理论等。

以上是基于GoogleNet的动物种类识别算法的基本原理和数学公式。由于这个领域的研究和实践仍在不断发展，可能会有更先进的模型和算法被开发出来。