2023 ABC题目+初步想法
- 写在最前面
- A题:定日镜场的优化设计
- 问题1:建模将其抽象为数学公式
- 问题2:固定部分参数,约束条件下的局部最优化问题
- 可尝试方法
- 问题3:约束条件下的局部最优化问题
- 附录:相关计算公式
- 参考文献
- B题:多波束测线问题
- 问题1:(平面)建模将其抽象为数学公式(比A稍微简单)
- 问题2:(三维空间)建模将其抽象为数学公式
- 问题3:在2的基础上,约束条件的最优化问题(也比A好做)
- 问题4:
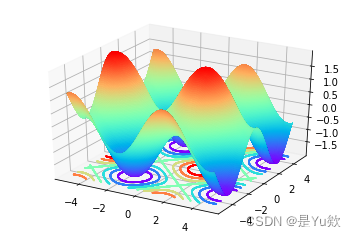
- 论文绘图亮点:绘制三维图、等高线图
- C题:蔬菜类商品的自动定价与补货决策(之后可能详细更新,看其他任务顺不顺利hh)
- 附件
- 问题1:挖掘关联关系,可参考https://blog.csdn.net/wtyuong/article/details/124769657
- 问题一方案
- 问题2:(品类一周)时间序列预测+最优化
- 问题3:(单品一天)短周期序列预测+双目标最优化
- 问题4:文献调研+文字建模
写在最前面
马上参加华为杯研数学建模了hh,找一下数模逻辑
看看今年本科有什么题目,随手记录下思路
A题:定日镜场的优化设计


附件数据:
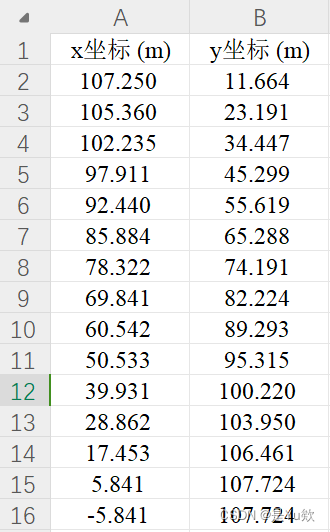
问题1:建模将其抽象为数学公式

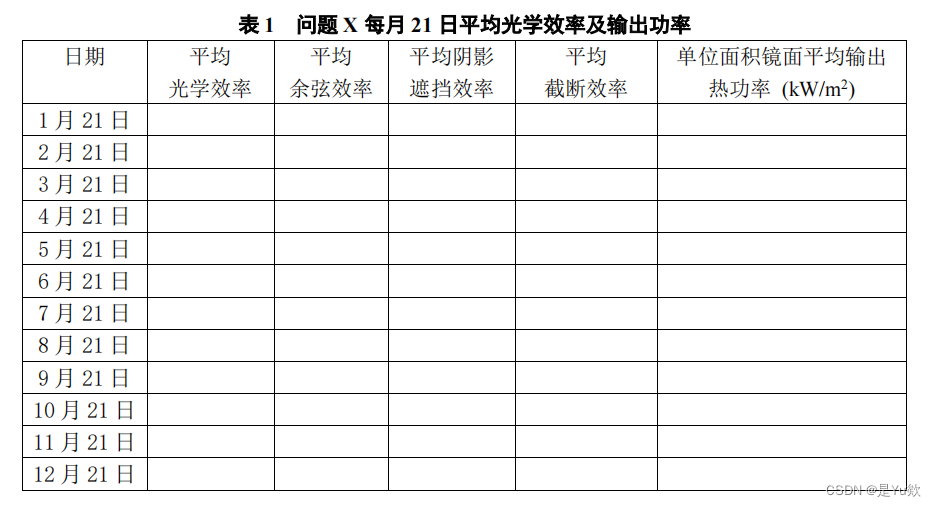

问题2:固定部分参数,约束条件下的局部最优化问题


result2.xlsx

可尝试方法
如果有条件(代码有一定难度),可以尝试启发式算法,如模拟退火、蚁群算法、遗传算法等,适用于非线性和非凸问题
如果不行,下面的方法也是思路之一
约束优化的优化器: 一些数值优化库和软件包,如MATLAB中的fmincon,Python中的scipy.optimize等,提供了专门用于处理约束优化问题的优化器。
问题3:约束条件下的局部最优化问题
如果不好入手,可以尝试问题简化:
先通过理论设计找到几个可能的最优尺寸、安装高度,然后转化为问题二


result3.xlsx

附录:相关计算公式


参考文献

B题:多波束测线问题
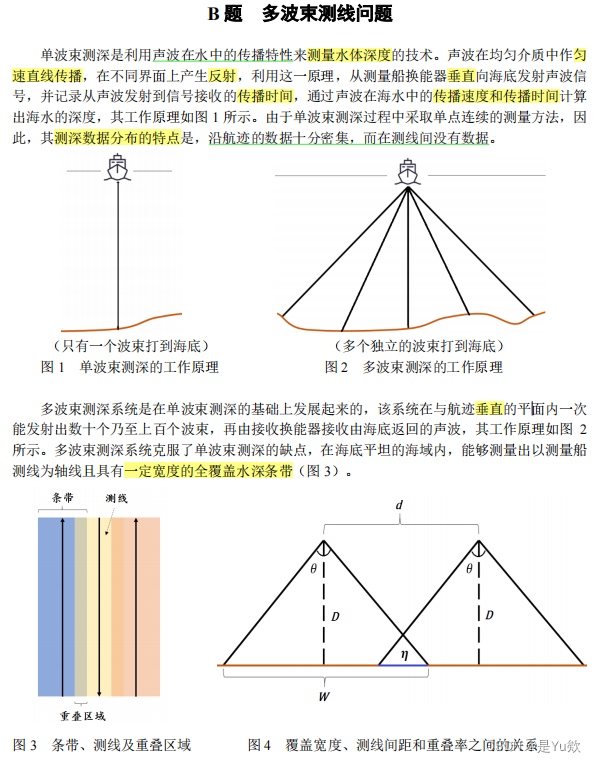
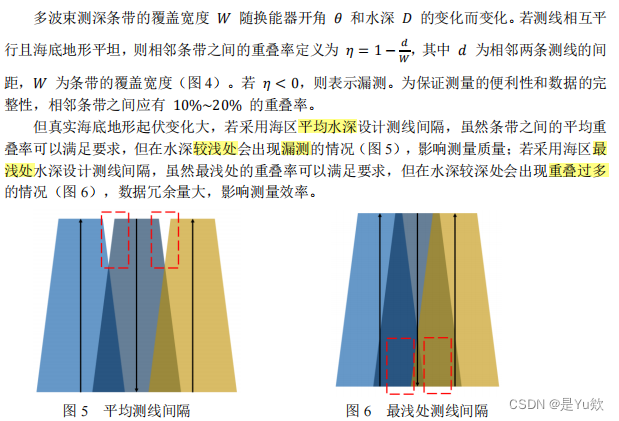
问题1:(平面)建模将其抽象为数学公式(比A稍微简单)
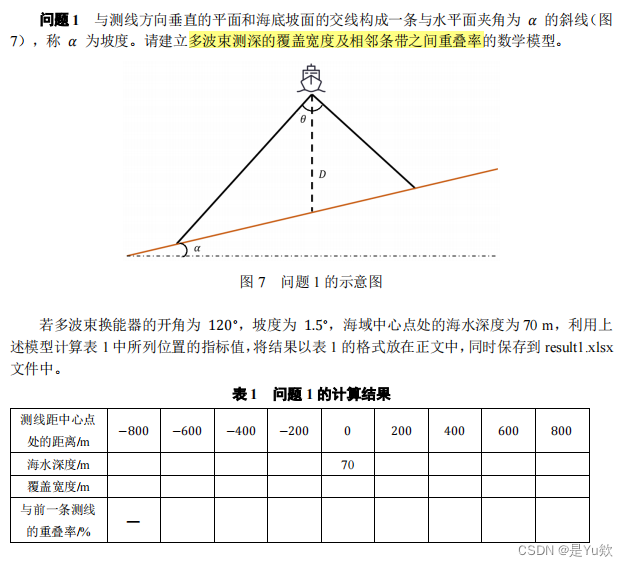
问题2:(三维空间)建模将其抽象为数学公式
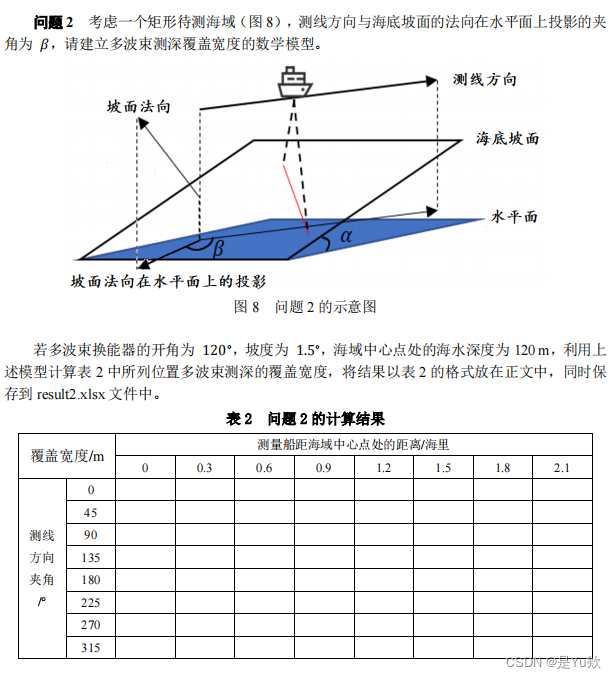
问题3:在2的基础上,约束条件的最优化问题(也比A好做)
目标函数:长度最短
约束条件:
1、完全覆盖
2、重叠率10-20

问题4:

附件数据:
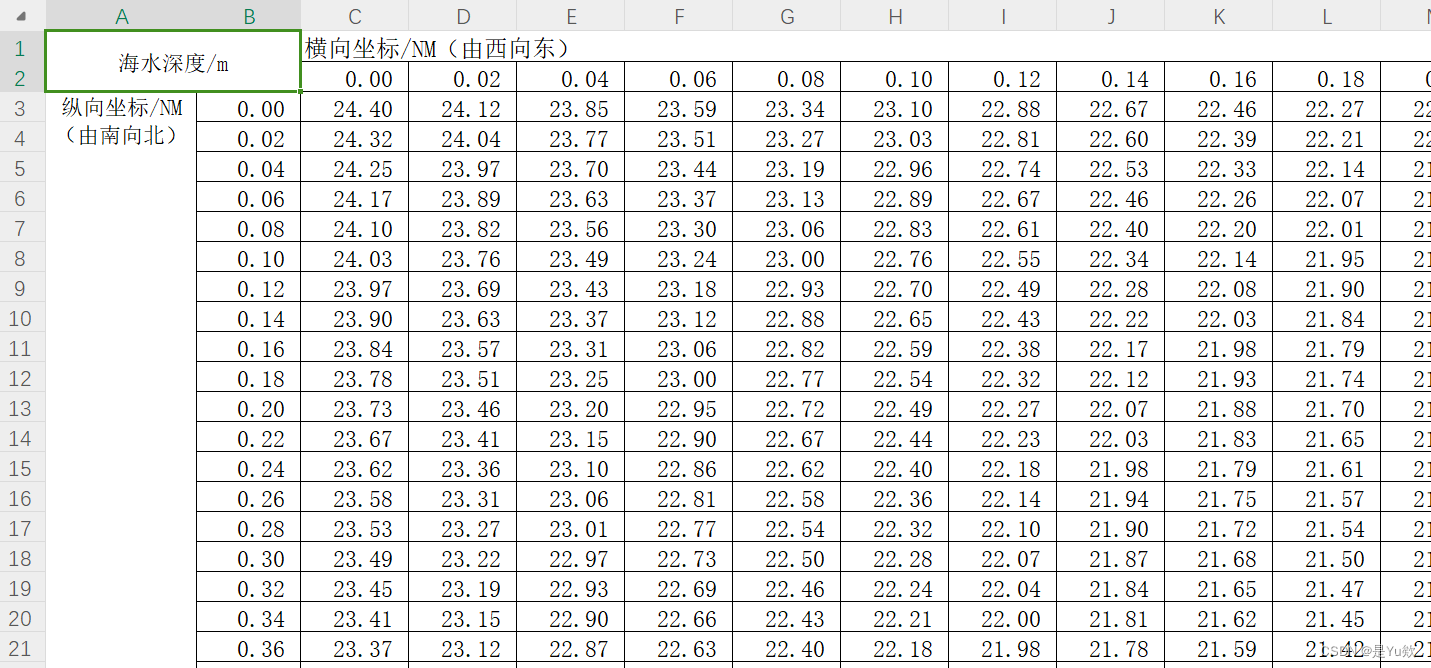
论文绘图亮点:绘制三维图、等高线图
可参考:https://blog.csdn.net/u014636245/article/details/82799573
C题:蔬菜类商品的自动定价与补货决策(之后可能详细更新,看其他任务顺不顺利hh)

附件

附件 1 给出了某商超经销的 6 个蔬菜品类的商品信息;
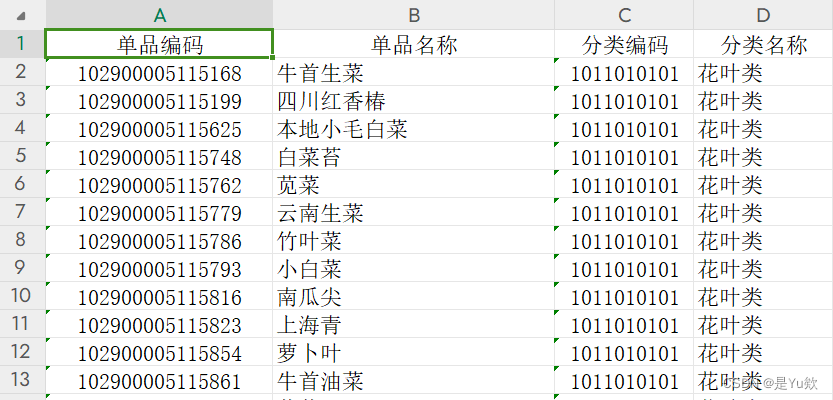
附件 2 和附件 3 分别给出了该商超 2020 年 7 月 1 日至 2023 年 6 月 30 日各商品的销售流水明细与批发价格的相关数据;
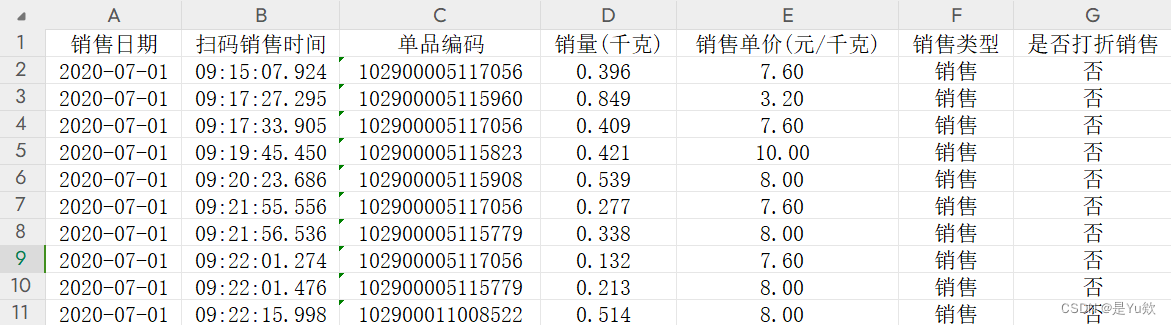
附件 4 给出了各商品近期的损耗率数据。
请根据附件和实际情况建立数学模型解决以下问题:
问题1:挖掘关联关系,可参考https://blog.csdn.net/wtyuong/article/details/124769657
问题 1 蔬菜类商品不同品类或不同单品之间可能存在一定的关联关系,请分析蔬菜各品类及单品销售量的分布规律及相互关系。
问题一方案
首先,附件1、附件2之间通过单品编码进行表连接
参考:https://blog.csdn.net/lost0910/article/details/104814860
根据实际情况,我觉着可以
df3 = pd.merge(df1,df2,on='key',how='right')
其中,df1为附件3,df2为附件2

1、各品类之间
2、单品销售量之间
也可以各品类及单品销售量两两之间
分布规律:
关联关系

问题2:(品类一周)时间序列预测+最优化
问题 2 考虑商超以品类为单位做补货计划,请分析各蔬菜品类的销售总量与成本加成 定价的关系,并给出各蔬菜品类未来一周(2023 年 7 月 1-7 日)的日补货总量和定价策略,使得商超收益最大。
问题3:(单品一天)短周期序列预测+双目标最优化
问题 3 因蔬菜类商品的销售空间有限,商超希望进一步制定单品的补货计划,要求:
1、可售单品总数控制在 27-33 个,
2、且各单品订购量满足最小陈列量 2.5 千克的要求。
根据 2023年 6 月 24-30 日的可售品种,给出 7 月 1 日的单品补货量和定价策略,
1、在尽量满足市场对各品类蔬菜商品需求的前提下,
2、使得商超收益最大。
问题4:文献调研+文字建模
问题 4 为了更好地制定蔬菜商品的补货和定价决策,商超还需要采集哪些相关数据,这些数据对解决上述问题有何帮助,请给出你们的意见和理由。