一.简介
异或,英文为exclusive OR,缩写成xor
异或(xor)是一个数学运算符。它应用于逻辑运算。异或的数学符号为“⊕”,计算机符号为“xor”。其运算法则为:
a⊕b = (¬a ∧ b) ∨ (a ∧¬b)
如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0。
异或也叫半加运算,其运算法则相当于不带进位的二进制加法:二进制下用1表示真,0表示假,则异或的运算法则为:0⊕0=0,1⊕0=1,0⊕1=1,1⊕1=0(同为0,异为1),这些法则与加法是相同的,只是不带进位,所以异或常被认作不进位加法。
异或略称为XOR、EX-OR
程序中有两种演算子:XOR、⊕。
使用方法如下:
z = x ⊕ y
z = x xor y
二.运算法则
- 归零律 : a⊕a=0
- 恒等律 : a⊕0=a
- 交换律 : a⊕b=b⊕a
- 结合律 : a⊕b⊕c=a⊕(b⊕c)=(a⊕b)⊕c
- 自反 : a⊕b⊕a=b
- d=a⊕b⊕c可以推出a=d⊕b⊕c
- 若x是二进制数0101,y是二进制数1011,则x⊕y=1110.只有在两个比较的位不同时其结果是1,否则结果为0.即“两个输入相同时为0,不同则为1”.
a b a⊕b 0 0 0 0 1 1 1 0 1 1 1 0
三.逻辑
逻辑表达式:F = AB' + A'B
异或逻辑的真值表如图1所示:
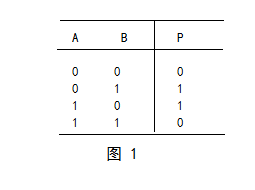
其逻辑符号如图2所示:
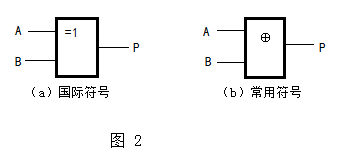
异或逻辑的关系是:当AB不同时,输出P=1;当AB相同时,输出P=0。“⊕”是异或运算符号,异或逻辑也是与或非逻辑的组合,其逻辑表达式为:
P=A⊕B
由图1可知,异或运算的规则是:
0⊕0=0,0⊕1=1
1⊕0=1,1⊕1=0
口诀1:
相同取0,相异取1
口诀2:
输入A取0,则输出p=输入B
输入A取1,则输出p=输入B的反
事实上,XOR 在英文里面的定义为either one (is one), but not both, 也即只有一个为真(1)时,取真(1)。
四.作用
在计算机中普遍运用,异或(xor)的逻辑符号一般用xor,也有用⊕的:
真⊕假=真
假⊕真=真
假⊕假=假
真⊕真=假
或者为:
True ⊕ False = True
False ⊕ True = True
False⊕ False = False
True ⊕ True = False
部分计算机语言用1表示真,用0表示假,所以两个字节按位异或如下
| 00000000 | |
| xor | 00000000 |
| ------------- | |
| 结果 | 00000000 |
下面是两个二进制数值进行异或计算:
| 11111111 | |
| xor | 00000000 |
| -------------- | |
| 结果 | 11111111 |
现实中用的都是十进制的数值,那么我们来看一看两个十进制数值是怎么进行异或计算:
5 ⊕ 3 = ?
1.进行异或计算前会把数值都转换为二进制:
5和3转为二进制分别为:0101 、0011
| 0101 | |
| xor | 0011 |
| -------- | |
| 结果 | 0110 |
2.再把结果 0110 转换为十进制的:6
3.所以 5 ⊕ 3 = 6
五.巧用
与其它语言不同,C语言和C++语言(C++支持xor,用法和效果如'^'相同)的异或不用xor,而是用“^”,键入方式为Shift+6。(而其它语言的“^”一般表示乘方)
若需要交换两个变量的值,除了通常使用的借用中间变量进行交换外,还可以利用异或,仅使用两个变量进行交换,如:
void swap(int &a,int &b)
{a=a^b;b=b^a;a=a^b;
}详解:
a1=a^bb=b^a1=b^a^b=a
//此时a1=a^b b=a
a=a1^a=a^b^a=b注意:
a=a^b^(b=a);//此类形式是不正确的UB行为,在不同编译器中会有不同的结果,切勿使用
这样就完成了a与b的交换。
综上:同一变量与另一变量和其异或值异或等于另一个数,如(a^b)^b=a。
用例:可使用于加密算法某一环节或更多环节,使算法更复杂,不易被破解,安全性更高。
六.与加减运算的关系
在伽罗华域上加减运算等价,即异或运算。而乘除直接进行多项式乘除然后对本原多项式取模。