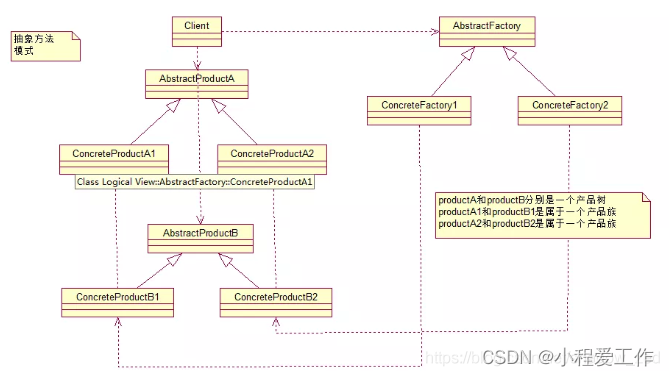
2848. 与车相交的点
核心思想:差分数组。统计覆盖区间,把nums中有的区间+1,维护区间我们用差分数组,然后求出差分数组的前缀和即是我们维护的区间,判断区间有哪些值是大于0的即可。
2849. 判断能否在给定时间到达单元格
核心思想:数学题,贪心做法,首先走斜线,然后走到终点看最短的路径是否小于等于t。

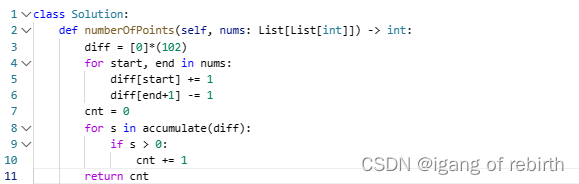
2850. 将石头分散到网格图的最少移动次数
核心思想:问题转换,全排列。其实这题思维不好想,就是把要拿出的石头坐标统计出来,那几个就统计几个,然后要拿入的统计出来,然后枚举它们的所有组合情况的最小值。全排列可以自己用回溯写,运行速度会快很多,这里我直接用库函数了。
2851. 字符串转换
核心思想:动态规划+KMP+矩阵快速幂,其实动态规划简单,主要是找到前一个动态和后一个动态的关系,然后具体怎么找的c可以看b站灵神的视频,这里只讲整体思路。