【C++模拟实现】手撕红黑树(含图解)
目录
- 【C++模拟实现】手撕红黑树(含图解)
- 红黑树的介绍(百度百科)
- 简介
- 特征(十分重要,红黑树的基础)
- 红黑树的实现代码(insert部分)
- 验证是否为红黑树
- 红黑树的图解
- 红黑树的正常情况: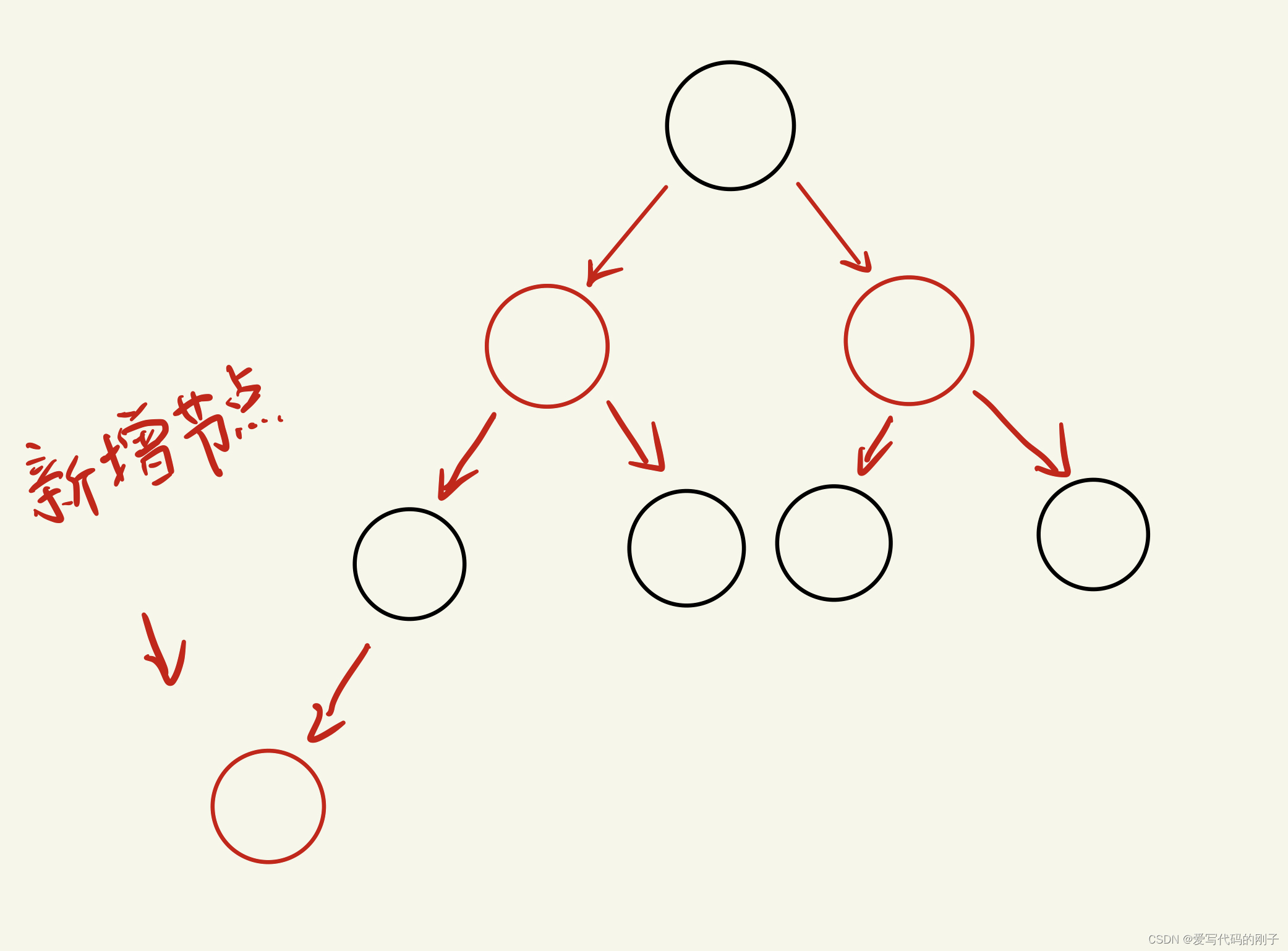
- 红黑树情况一(uncle节点为红色):
- 红黑树情况二(需要旋转的情况,uncle节点为黑色或者为空)
作者:爱写代码的刚子
时间:2023.9.11
前言:这次的博客除了红黑树的模拟实现外还附加了图示来帮助理解红黑树,以及编写代码对红黑树的验证。
红黑树的介绍(百度百科)
简介
-
红黑树是一种特定类型的二叉树,它是在计算机科学中用来组织数据比如数字的块的一种结构。
-
红黑树是一种平衡二叉查找树的变体,它的左右子树高差有可能大于 1,所以红黑树不是严格意义上的平衡二叉树(AVL),但 对之进行平衡的代价较低, 其平均统计性能要强于 AVL 。
-
由于每一棵红黑树都是一颗二叉排序树,因此,在对红黑树进行查找时,可以采用运用于普通二叉排序树上的查找算法,在查找过程中不需要颜色信息。
特征(十分重要,红黑树的基础)
红黑树是每个结点都带有颜色属性的二叉查找树,颜色或红色或黑色。 在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
**性质1. 结点是红色或黑色。 **
**性质2. 根结点是黑色。 **
性质3. 所有叶子都是黑色。(叶子是NIL结点)
性质4. 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
性质5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
是性质4导致路径上不能有两个连续的红色结点确保了这个结果。最短的可能路径都是黑色结点,最长的可能路径有交替的红色和黑色结点。因为根据性质5所有最长的路径都有相同数目的黑色结点,这就表明了没有路径能多于任何其他路径的两倍长。
因为红黑树是一种特化的二叉查找树,所以红黑树上的只读操作与普通二叉查找树相同。
红黑树的实现代码(insert部分)
#include <iostream>
using namespace std;
enum Colour
{BLACK,RED
};template<class K,class V>
struct RBTreeNode
{RBTreeNode(const pair<K,V>& kv):_left(nullptr),_parent(nullptr),_right(nullptr),_c(RED)//初始为红节点,_kv(kv){}RBTreeNode* _left;RBTreeNode* _parent;RBTreeNode* _right;Colour _c; pair<K,V> _kv;};template<class K,class V>
class RBTree
{typedef RBTreeNode<K,V> Node;
public:RBTree():_root(nullptr){}bool insert(const pair<K,V>& kv){if(_root==nullptr){_root=new Node(kv);_root->_c=BLACK;return true;}else{Node* cur=_root;Node* parent=nullptr;while(cur){if(cur->_kv.first>kv.first){parent=cur;cur=cur->_left;}else if(cur->_kv.first<kv.first){parent=cur;cur=cur->_right;}else{return false;}}cur=new Node(kv);if(parent->_kv.first>kv.first){parent->_left=cur;}else{parent->_right=cur;}cur->_parent=parent;//需要调整的情况while(parent&&parent->_c==RED){Node* grandfather=parent->_parent;if(grandfather->_left==parent){Node* uncle=grandfather->_right;//判断uncle的几种情况if(uncle&&uncle->_c==RED){uncle->_c=parent->_c=BLACK;grandfather->_c=RED;cur=grandfather;parent=cur->_parent;}else {if(cur==parent->_left){_RotateR(grandfather);grandfather->_c=RED;parent->_c=BLACK;}else{_RotateL(parent);_RotateR(grandfather);grandfather->_c=RED;cur->_c=BLACK;}break;}}else{Node* uncle=grandfather->_left;if(uncle&&uncle->_c==RED){uncle->_c=parent->_c=BLACK;grandfather->_c=RED;cur=grandfather;parent=cur->_parent;}else {if(cur==parent->_right){_RotateL(grandfather);parent->_c=BLACK;grandfather->_c=RED;}else{_RotateR(parent);_RotateL(grandfather);cur->_c=BLACK;grandfather->_c=RED;}break;}}}}_root->_c=BLACK;//头节点始终为黑色return true;}void _RotateR(Node* parent){Node*cur=parent->_left;Node*curRight=cur->_right;Node*ppnode=parent->_parent;cur->_right=parent;parent->_left=curRight;if(curRight){curRight->_parent=parent;}parent->_parent=cur;//处理ppnodeif(parent==_root){_root=cur;cur->_parent=nullptr;}else{if(ppnode->_left==parent){ppnode->_left=cur;}else{ppnode->_right=cur;}cur->_parent=ppnode;}}void _RotateL(Node* parent){Node* cur=parent->_right;Node* curLeft=cur->_left;Node* ppnode=parent->_parent;cur->_left=parent;parent->_right=curLeft;if(curLeft){curLeft->_parent=cur;}parent->_parent=cur;if(parent==_root){_root=cur;cur->_parent=nullptr;}else{if(ppnode->_left==parent){ppnode->_left=cur;}else{ppnode->_right=cur;}cur->_parent=ppnode;}}private:Node* _root;
};验证是否为红黑树
bool CheckColour(Node* root, int blacknum, int benchmark)//并不是最优递归
{if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_c == BLACK){++blacknum;}if (root->_c == RED && root->_parent && root->_parent->_c == RED){cout << root->_kv.first << "有连续红色节点" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark)&& CheckColour(root->_right, blacknum, benchmark);
}
bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr)return true;if (root->_c != BLACK){return false;}// 基准值int benchmark = 0;Node* cur = _root;while (cur){if (cur->_c == BLACK)++benchmark;cur = cur->_left;}return CheckColour(root, 0, benchmark);}
- 添加以上成员函数可以来验证该红黑树的黑节点数量是否正确,以及是否出现连续红色节点。
- 以下为测试代码:

红黑树的图解
红黑树的正常情况:
红黑树情况一(uncle节点为红色):
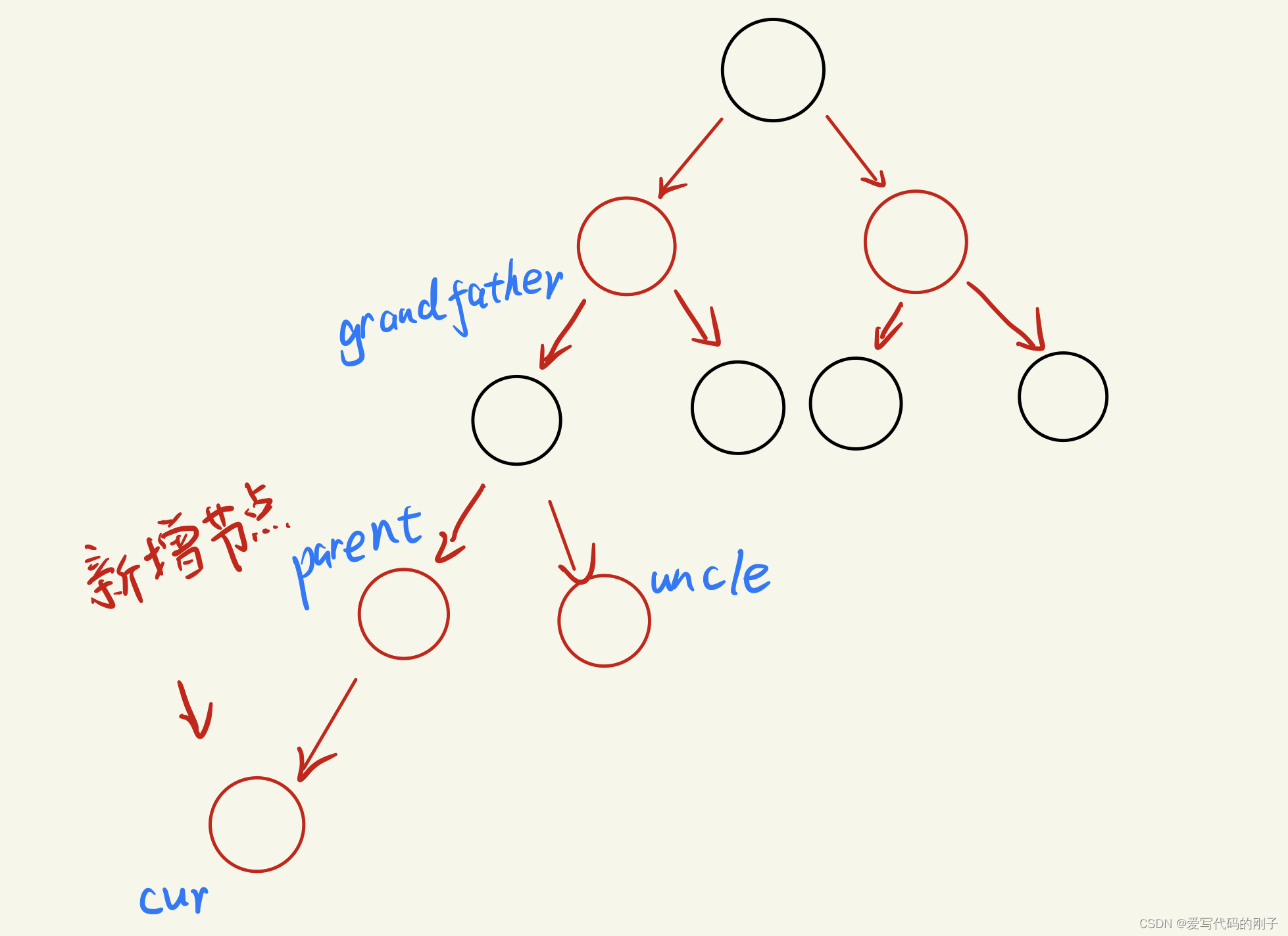
-
由于不能出现连续的红色节点,所以我们需要进行处理,此时我们有以下结论:
当parent为RED节点时说明我们插入了一个节点(红黑树默认插入RED节点)导致出现了连续的红色节点
当uncle节点存在且为红,我们需要将parent和uncle节点变为黑色,将grandfather变为红色
最后将grandfather赋值给cur,parent指向cur的_parent,进入下一个循环,直到parent为黑色节点
红黑树情况二(需要旋转的情况,uncle节点为黑色或者为空)
-
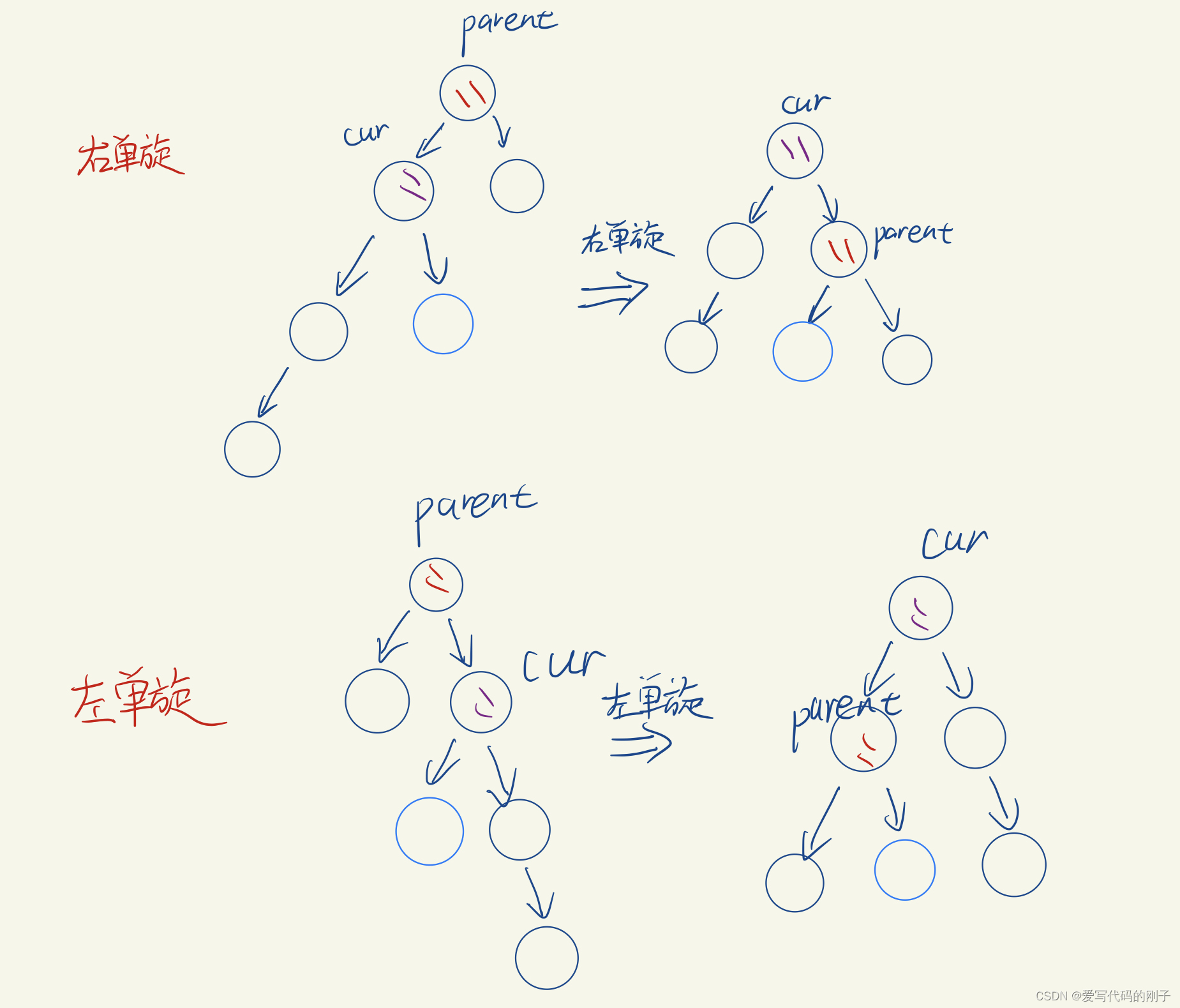
parent为grandfather的左节点,且cur为parent的左节点(右单旋)
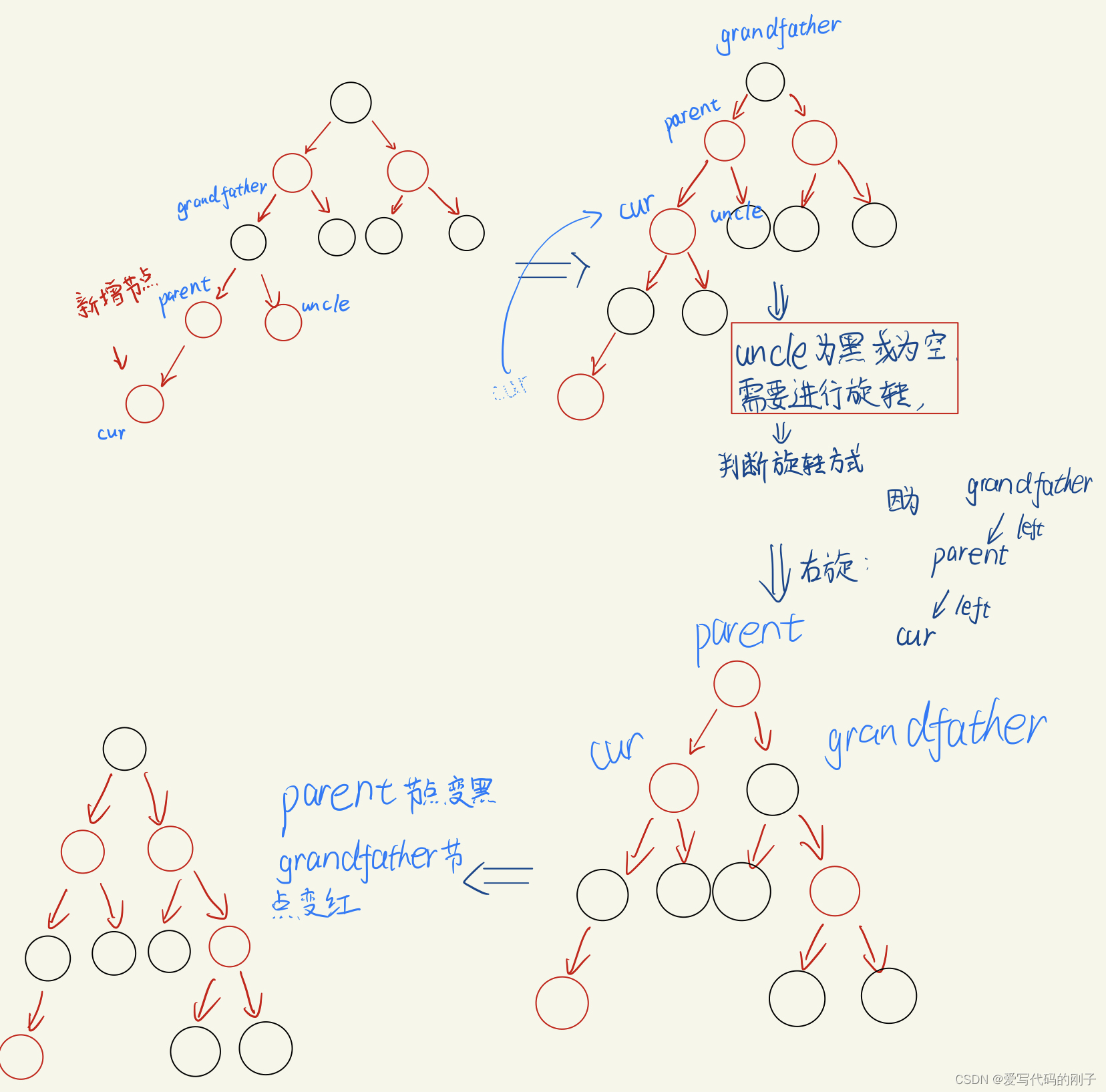
-
parent为grandfather的右节点,且cur为parent的右节点(左单旋)
原理和右单旋几乎相同,图略。
-
parent为grandfather的右节点,且cur为parent的左节点(右左双旋)
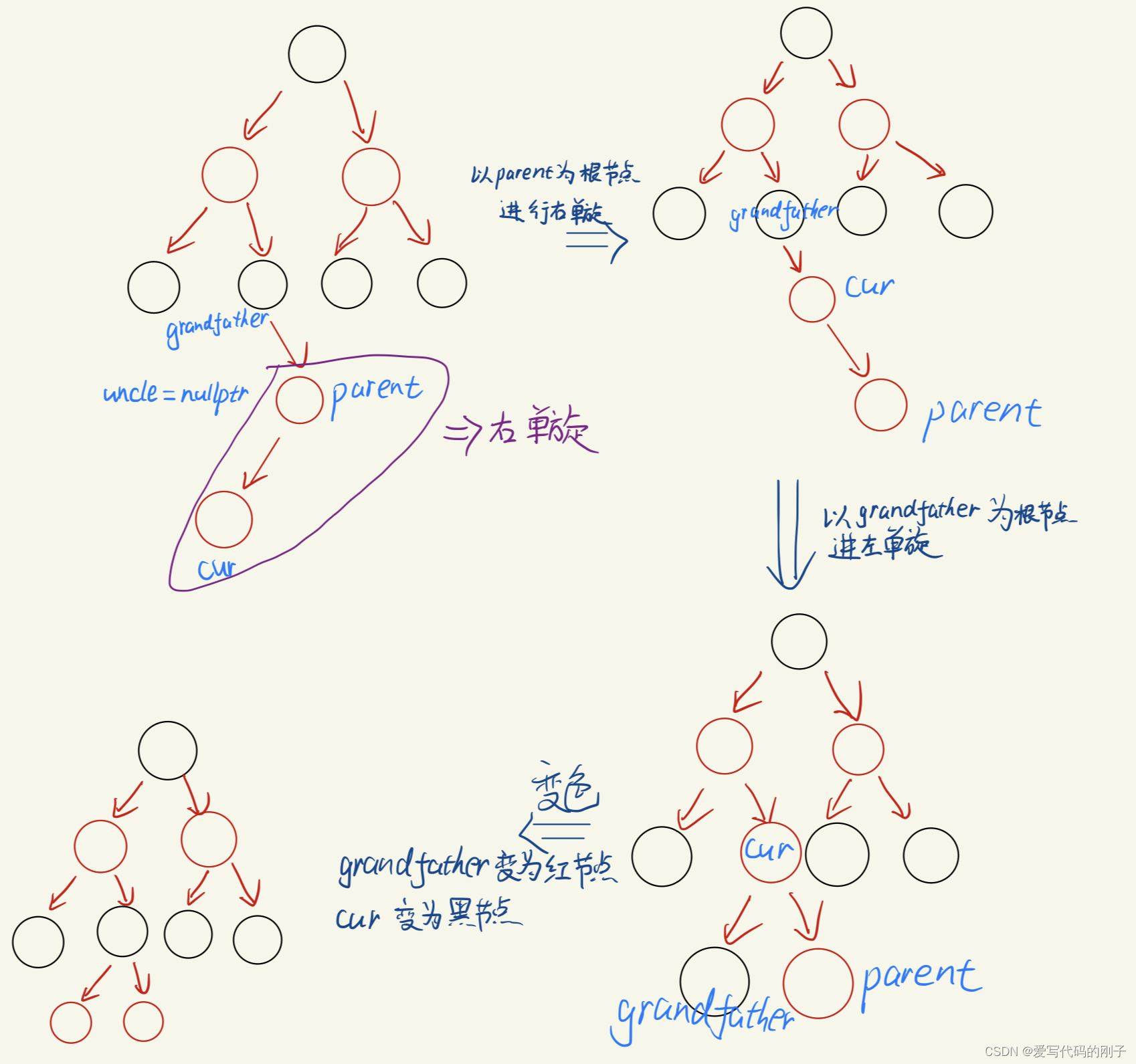
-
parent为grandfather的左节点,且cur为parent的右节点(左右双旋)
原理和右左双旋几乎相同,图略。
附:
- 降序插入构建红黑树动图:
- 左右旋转的成员函数复用了avl树的旋转函数。
- 左右旋转图解: