💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃个人主页 :阿然成长日记 👈点击可跳转
📆 个人专栏: 🔹数据结构与算法🔹C语言进阶
🚩 不能则学,不知则问,耻于问人,决无长进
🍭 🍯 🍎 🍏 🍊 🍋 🍒 🍇 🍉 🍓 🍑 🍈 🍌 🍐 🍍
文章目录
- 一、树的概念与定义
- 二、树的有关名词
- 三、树的存储结构
- 1.双亲表示法
- 2.孩子表示法
- 3.孩子兄弟表示法(又叫二叉树法)
- 四、树的应用
一、树的概念与定义
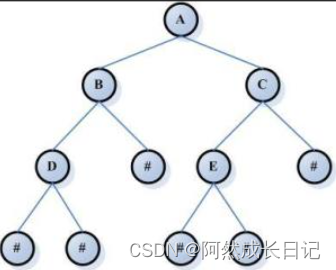
把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 树是一种非线性的数据结构,它表现的关系是一对多它是由
n(n>=0)个结点组成的有限集,当n = 0时,称为空树。
在任意一棵非空树中应满足:🔸1.有且仅有一个特殊的根节点,根节点没有前驱结点
🔸2.每一个非根结点有且只有一个父结点;
🔸3.除了根结点外,每个子结点可以分为多个不相交的子树,并且子树是不相交的🔸4.树是递归定义的
🔸 5.一颗N个结点的树有N-1条边

二、树的有关名词
就拿下面这颗树来举例:
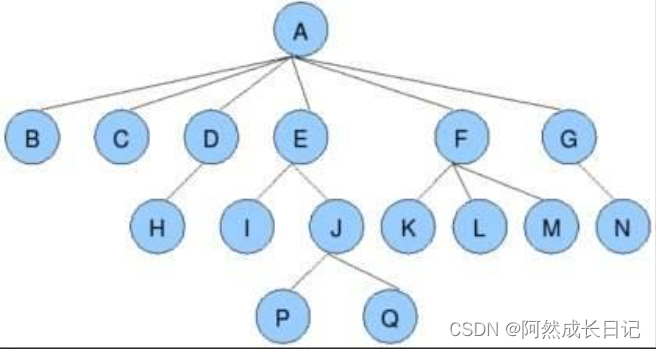
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点.
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
注意:节点和双亲结点为社么这样叫?就是因为引起对性别的歧视。既要尊重男性,也要尊重女性。
三、树的存储结构
(1)双亲表示法(2)孩子表示法(3)孩子兄弟表示法
1.双亲表示法
链式存储中在每个节点中,有一个指示器指示其双亲结点到链表中的位置,
使其每个结点,不但知道自己是谁,而且知道双亲位置
不能查找子节点,只能查找双亲结点。
1)链式存储
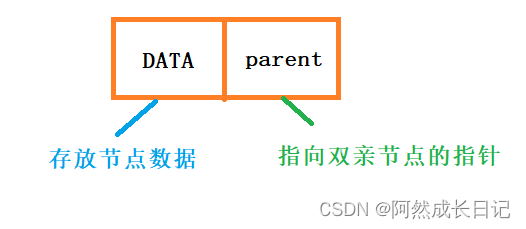
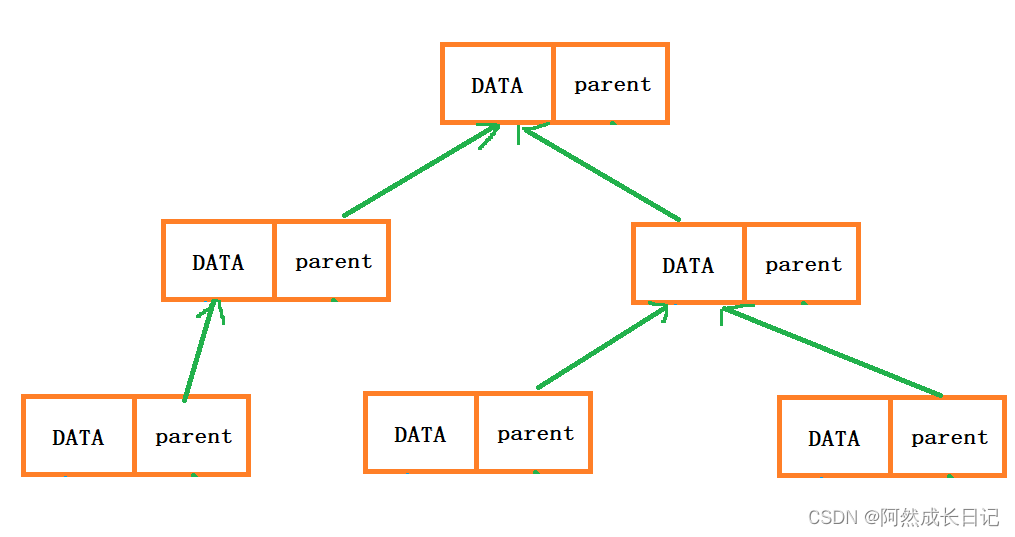
2)数组存储
采用数组中存放结构体。
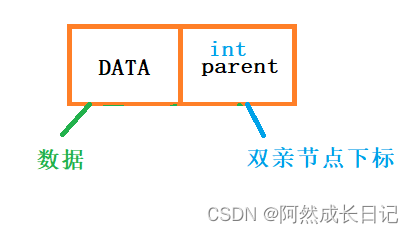

2.孩子表示法
将每个结点的孩子结点排序,以单链表存储,则n个结点有n个孩子链表 并且如果是叶子结点,这个单链表为空然后将每个单链表的头指针组成一个线性表,顺序存储放入数组中
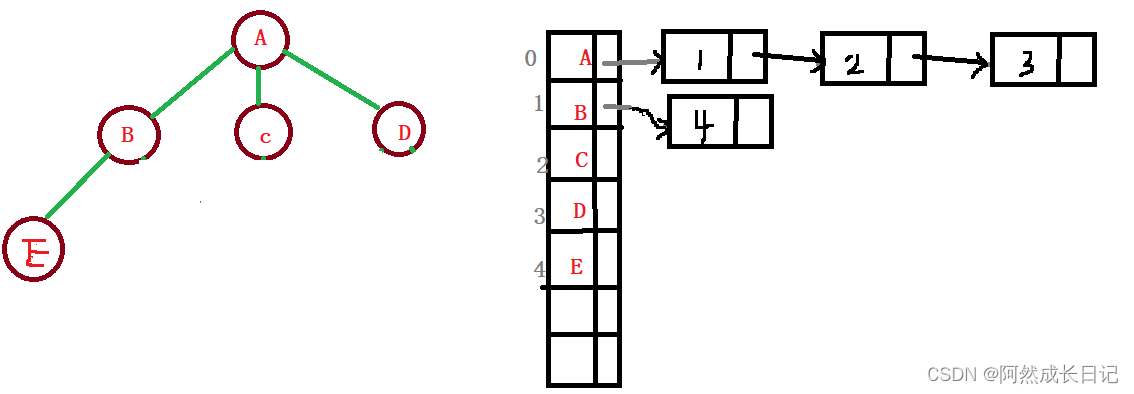
3.孩子兄弟表示法(又叫二叉树法)
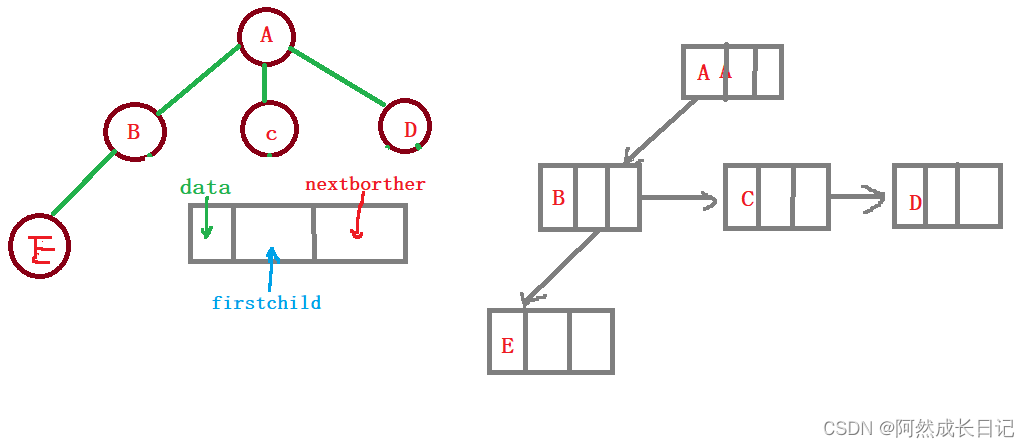
对于树来说,他的最好的存储方式是兄弟节点表示法
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
四、树的应用