Mini-Batch梯度下降法

在开始Mini-Batch算法开始之前，请确保你已经掌握梯度下降的最优化算法。

在训练神经网络时，使用向量化是加速训练速度的一个重要手段，它可以避免使用显式的for循环，并且调用经过大量优化的矩阵计算函数库。但是当数量增加到一定级别的时候，比如说五百万、五千万或者更大，此时此刻即便是进行了向量化，其训练速度也是挺慢的。Mini-Batch最优化算法则可以加速这种情况下的训练过程。

字如其名，Mini-Batch梯度下降法就是将数据集划分为若干个更小的数据集（Mini-Batch），然后依次对小规模数据集进行处理。假设每一个子集中只有1000个数据样本，那么在总样本量为500万的时候，会被分为5000个子集。原数据集的特征部分为$x^{(1)},x^{(2)},x^{(3)}...x^{(1000)},x^{(1001)}....x^{(m)}$，现在被划分为:
X { 1 } = x ( 1 ) , x ( 2 ) , x ( 3 ) . . . x ( 1000 ) X { 2 } = x ( 1001 ) , x ( 1002 ) , x ( 1003 ) . . . x ( 2000 ) X { 3 } = x ( 2001 ) , x ( 2002 ) , x ( 2003 ) . . . x ( 3000 ) X^{\{1\}}=x^{(1)},x^{(2)},x^{(3)}...x^{(1000)}\\ X^{\{2\}}=x^{(1001)},x^{(1002)},x^{(1003)}...x^{(2000)}\\ X^{\{3\}}=x^{(2001)},x^{(2002)},x^{(2003)}...x^{(3000)} X{1}=x(1),x(2),x(3)...x(1000)X{2}=x(1001),x(1002),x(1003)...x(2000)X{3}=x(2001),x(2002),x(2003)...x(3000)
其中 X { i } X^{\{i}\} X{i}表示第i个Mini-Batch的样本集
同样地，标签集也被划为5000个子集，分别是
Y { 1 } = y ( 1 ) , y ( 2 ) , y ( 3 ) . . . y ( 1000 ) Y { 2 } = y ( 1001 ) , y ( 1002 ) , y ( 1003 ) . . . y ( 2000 ) Y { 3 } = y ( 2001 ) , y ( 2002 ) , x ( 2003 ) . . . x ( 3000 ) Y^{\{1\}}=y^{(1)},y^{(2)},y^{(3)}...y^{(1000)}\\ Y^{\{2\}}=y^{(1001)},y^{(1002)},y^{(1003)}...y^{(2000)}\\ Y^{\{3\}}=y^{(2001)},y^{(2002)},x^{(2003)}...x^{(3000)} Y{1}=y(1),y(2),y(3)...y(1000)Y{2}=y(1001),y(1002),y(1003)...y(2000)Y{3}=y(2001),y(2002),x(2003)...x(3000)
其中 Y { i } Y^{\{i}\} Y{i}表示第i个Mini-Batch的标签集

一个完整的Mini-Batch子集由标签子集和样本子集构成，第i个Mini-Batch子集等于 ( X { i } , Y { i } ) (X^{\{i\}},Y^{\{i\}}) (X{i},Y{i})
接下来说一下向量化表示，假设一个样本有n个特征，一个Mini-Batch有m个样本，那么他的KaTeX parse error: Expected 'EOF', got '}' at position 2: X}̲应该是一个m行n列的矩阵，他的Y是一个m行1列的矩阵

划分完自己之后，然后我们会单独处理各个Mini-Batch子集。比如说先前向传播，然后计算代价函数，根据代价函数反向传播求出梯度下降中的导数，然后使用梯度下降进行计算。就和一个神经网络差不多，不是吗？总的来说就是训练规模较大的神经网络的时候，我们应该将他们切分为若干个较小的子集，然后让各个子集独立地进行神经网路的训练，就是这样。

在传统的梯度下降中（左图），代价函数cost应该随着迭代的进行而逐渐下降；但是在Mini-Batch中就不一样了，他的cost函数会有一定的波动，但是整体应该是向下的（右图）

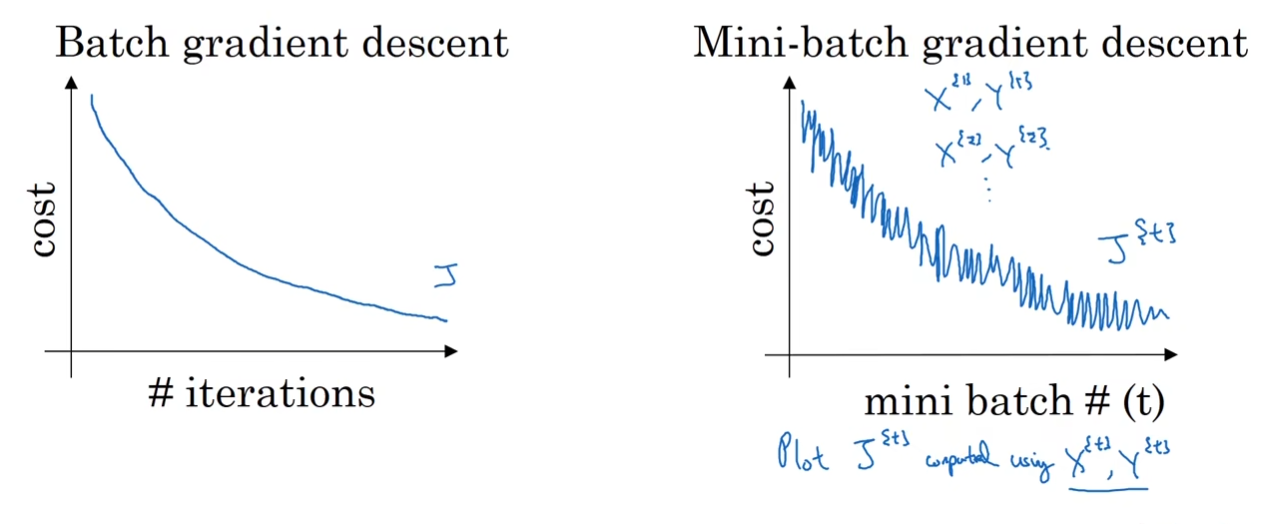
此外，需要我们个人决定的一个关键参数是Mini-Batch的大小，假设如果将一个数据集只划分为1个Mini-Batch，那么实际上他就是普通的梯度下降法，这是情况1；另一个极端是，一个Mini-Batch中只有一个样本，每个样本就是一个Mini-Batch，这种情况下的算法称之为随机梯度下降，这是情况2。

在情况1中，其实就是普通的梯度下降，他下降会十分“顺滑”，这是因为相对噪音比较小，但是对样本量大的情况来说，他将会相当耗时（蓝线）。而在情况2中，因为每个样本都是单独的Mini-Batch，大多数时候会朝着最小值前进，但是有一些样本是噪声样本，因此偶尔会指向错误的方向，因此这会使得其路线十分的九转十八弯（紫线）。而且他不会稳定收敛于一个点，而是在最小值的周围反复打转

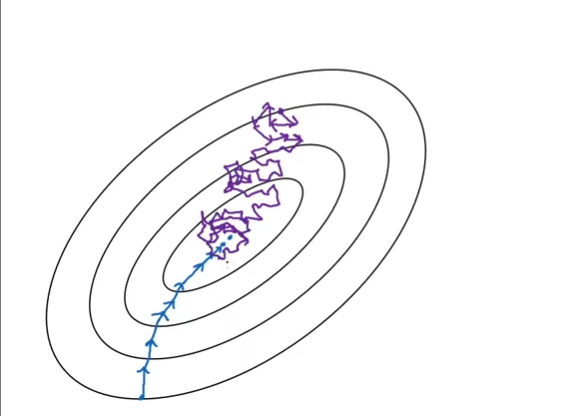
上述的两个极端例子我们可以知道，当Mini-Batch子集设计的太大的时候，虽然噪声少，下降较为顺滑，但是会有较大的时间开销；反之，较小的子集会导致噪声较大，下降的精度不高，但是单次训练速度快，而且较小的子集也无法充分来自于向量化的训练加速，总训练时间反而不是最快的。在实际中，选择适中的子集大小能够保证一定的精度，也能提高速度，并且利用好向量化带来的加速，在此基础之上，根据自己的目标选择合适的子集大小，平衡好训练速度和精度问题