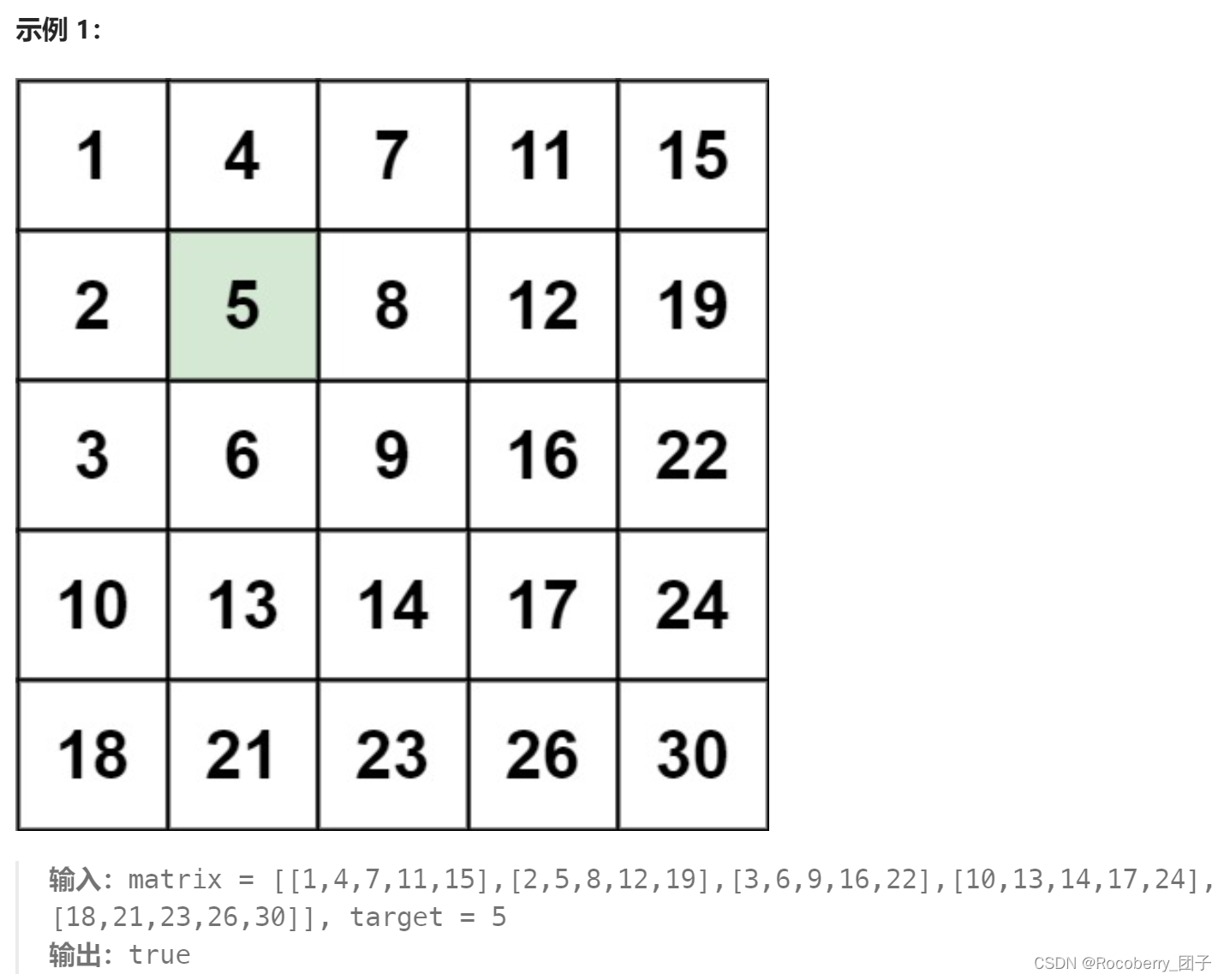
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列
• 每列的元素从上到下升序排列
  
  

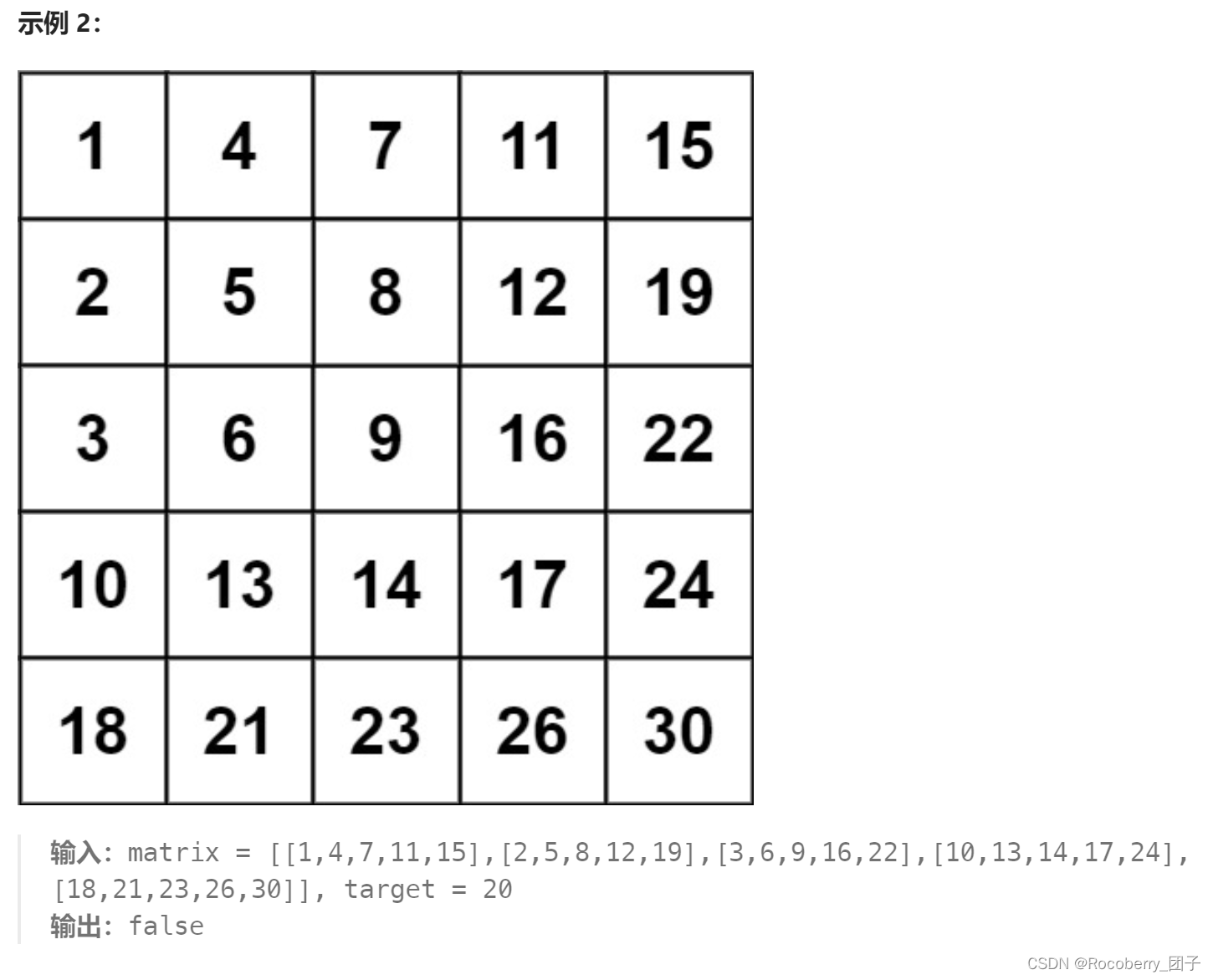
提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• $-10^9$ <= matrix[i][j] <= $10^9$
• 每行的所有元素从左到右升序排列 每列的所有元素从上到下升序排列
• $-10^9$ <= target <= $10^9$

题解1 对角线上下循环搜索（超时）

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {const int row = matrix.size();const int column = matrix[0].size();int km = min(row, column);if(1 == row){for(int i = 0; i < column; i++){if(target == matrix[0][i])return 1;else if(! i && target < matrix[0][i])return 0;}}else if(1 == column){for(int i = 0; i < row; i++){if(target == matrix[i][0])return 1;else if(! i && target < matrix[i][0])return 0;}}else{for(int i = 0; i < km; i++){if(target == matrix[i][i])return 1;else if(target < matrix[i][i]){if(! i) return 0;else{// 剪枝失败// 搜索空间只有 matrix[<i][<j]// 行for(int k = 0; k < i; k++)for(int l = 0; l < column; l++)if(target == matrix[k][l])return 1;// 列for(int k = 0; k < i; k++)for(int l = 0; l < row; l++)if(target == matrix[l][k])return 1;}}}}return 0;}
};

生气！！无脑循环都不超时

// 整理思路
// 应该从第一行最大值开始比较，不要纠结在对角线上
// 根据数据特点剪枝（缩小搜索空间）
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {const int row = matrix.size();const int column = matrix[0].size();int i(0), j(column-1);while(i < row && j >= 0){if(target == matrix[i][j]) return 1; else if(target > matrix[i][j]) i ++;else j --;}return 0;}
};

题解2 无脑循环

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {for (const auto& row: matrix) {for (int element: row) {if (element == target) {return true;}}}return false;}
};

题解3 学习STL(二分查找)

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {for (const auto& row: matrix) {// 二分查找auto it = lower_bound(row.begin(), row.end(), target);if (it != row.end() && *it == target) {return true;}}return false;}
};