2023年数维杯数学建模
B题 节能列车运行控制优化策略
原题再现:
在城市交通电气化进程快速推进的同时,与之相应的能耗增长和负面效应也在迅速增加。城市轨道交通中的快速增长的能耗给城轨交通的可持续性发展带来负担。2018 年,北京、上海、广州地铁负荷占全市总负荷的 1.5%-2.5%,成为了城市电网的最大单体负荷[1]。在“双碳”政策下,城轨系统换用 ATO 驾驶模式、光伏+地铁等方法都取得了较好的减碳节能效果。城轨系统的需求侧响应可以在保证乘客满意度的情况下降低牵引能耗成本[2],可进一步发掘城轨系统减碳节能的潜力。
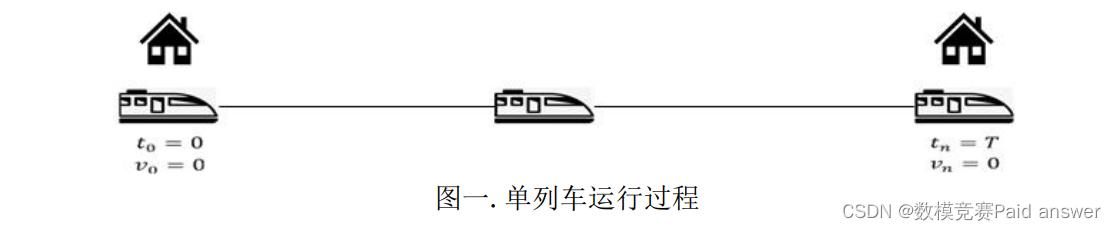
在列车运行过程中,列车与外界会产生各种摩擦,进而消耗列车牵引的能量。列车运行过程中,被考虑的因素较多,如列车与轨道的摩擦、列车受到的空气阻力、列车势能的变化、列车运行过程中的位置限速等。在同一段旅途中,列车使用不同的驾驶策略通常会产生不同的能量和时间的消耗。单列车在两个站台之间的运行过程如图一所示。
问题1
假设一辆列车在水平轨道上运行,从站台A运行至站台B,其间距为5144.7m,运行的速度上限为100km/h,列车质量为176.3t,列车旋转部件惯性的旋转质量因数p= 1.08,列车电机的最大牵引力为310KN,机械制动部件的最大制动力为760KN。列车受到的阻力满足Davis阻力方程f = 2.0895 + 0.0098v + 0.006v^2,该公式中的速度单位为m/s,阻力单位为KN。
你如何通过建模方法编写程序以获得列车运行过程的速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线与能量消耗-距离曲线?程序的运行时间是多长?需要获取列车以最短时间到达站台B、在最短运行时间上分别增加10s、20s、50s、150s、300s到达站台B总共六组曲线。
在列车运行的实际情况中,需要考虑的因素更多,模型也更加复杂。列车运行的旅途中不同的路段的限速是不同的,旅途中亦有不同的坡度情况,电机的动态特性也更加复杂,此外,储能装置在列车节能领域有着重要的应用,列车制动时,会将一定比例的能量储存至储能装置中,以待后续使用。如图二所示。
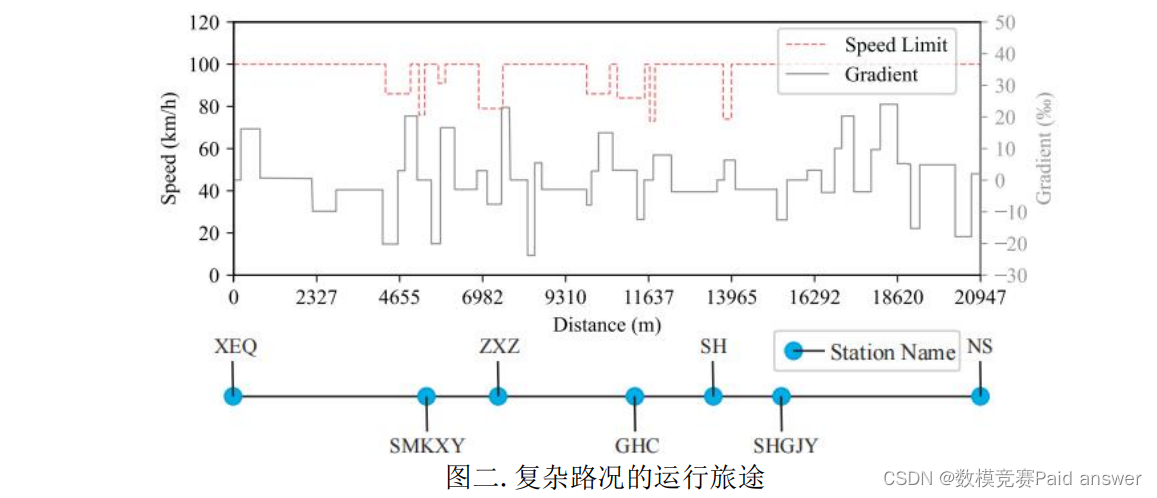
本赛题提供两个附件。从 XEQ 站至 SMKXY 站的路况数据与包含电机牵引/制动动态特性的列车相关参数数据。介绍如下:
附件一:从 XEQ 站至 SMKXY 站的路况数据(xls 格式),其包含 XEQ 站到 SMKXY站的路途中的坡度变化信息以及限速变化信息。详情见附件一.xls。

附件二:附件二介绍了电机的动态特性与参数并给出了静态电机牵引率与制动再生率。详情见附件二.docx。
问题 2
考虑附件一、二的路况信息以及电机的复杂动态过程。若列车计划运行时间为 T,请你设计优化方案得到可行的速度轨迹,使得运行过程的能耗降低(越低越好)。参照问题一,获取列车以最短时间到达站台 B、在最短运行时间上分别增加 10s、20s、50s、150s、300s 到达站台 B 总共六组曲线。
列车在运行过程中可能会出现各种突发情况导致列车需要提前到达站台或延时到达站台。列车的运行速度轨迹需要根据新的到站时间而发生变化。
问题 3。
列车从起点出发,原计划于 320s 后到达终点,列车运行至 2000m 位置时,由于前方突发事故,需要延迟 60s 到达终点。请你设计优化方案在保持列车节能运行下,能够快速地(越快越好)得到调整后的优化速度轨迹。作出列车运行过程的速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线与能量消耗-距离曲线。
整体求解过程概述(摘要)
针对问题一,以城市轨道交通电气化进程中能耗增长为背景,以欧拉数值法为基础,建立了模拟列车运行过程的动力学模型。通过考虑列车与轨道的摩擦、空气阻力、势能变化以及位置限速等因素,获取列车的速度-距离曲线、牵引力制动力-距离曲线、时间-距离曲线以及能量消耗-距离曲线。在模型中,我们考虑运行在水平轨道上的列车,通过给定站台 A 到站台 B 的距离、速度上限、列车质量、旋转部件惯性质量因数、列车电机最大牵引力和机械制动部件最大制动力,设定初始条件、定义微分方程,利用欧拉数值法进行迭代更新,得到了列车的运行状态。根据程序模拟运行结果,可观察到列车在不同路段内的速度变化、牵引制动力的变化、运行时间以及能量消耗。此外,还模拟运行在不同时间限制下列车到达站台 B 的情况,得到了六组曲线数据。
针对问题二,在对列车运行过程建立的动力学模型的基础上,可以使用粒子群优化算法来求解列车在给定路段上的最优速度轨迹。为了保证安全性和节能减排目标,在目标函数中我们将能耗消耗作为约束条件,并且根据路段坡度信息对最大速度进行限制。在粒子群算法中,通过计算该速度轨迹的能耗消耗来确定各个速度的适应度。为了更加准确地估计列车的能耗,我们需要考虑列车运行过程中的变速运动。通过计算列车在不同速度下的牵引功率和制动功率,在满足最大牵引力和最大制动力的情况下,确定列车在每个时间段内的加速度和制动度。然后,根据牵引功率和制动功率计算每个时间段的能耗,最终求得整段路程的总能耗。
针对问题三,介绍了两种优化方法解决问题三:建立速度曲线进行算法优化、采用分阶段求解路程和遗传算法。同时需要根据实时情况进行动态调整和优化,以确保列车安全、节能、快速地到达终点站。
问题分析:
问题一的分析
对问题 1 研究的意义的分析:问题 1 属于列车运行过程的数学建模问题。通过建立数学模型,可以获得列车在不同条件下的运行速度、牵引制动力、时间和能量消耗等曲线。这有助于了解列车在不同情况下的性能表现,为优化列车运行提供依据。
对于解决此类问题一般数学方法的分析:针对列车运行过程中的速度、牵引制动力、时间和能量消耗等变化,我们可以使用数值方法进行建模和求解。其中,欧拉数值法是一种常用的数值方法,适用于对微分方程进行数值近似求解。
对题目中所给数据特点的分析:附件中给出了列车在水平轨道上的运行数据,包括列车间距、速度上限、列车质量、惯性旋转质量因数、最大牵引力、最大制动力以及阻力方程。这些数据反映了列车运行过程中的关键参数和限制条件,是建立数学模型的基础。
对问题 1 的题目要求进行分析:问题 1 要求通过建模方法编写程序,获得列车最短运行时间下的速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线和能量消耗-距离曲线,以及程序的运行时间。这些曲线能够描述列车在不同位置的运行状态和能耗情况,有助于评估列车的性能和效率。此外,还需获取列车以最短时间到达站台 B、在最短运行时间上分别增加 10s、20s、50s、150s、300s 到达站台 B 总共六组曲线。
由于以上原因,我们首先建立一个基于欧拉数值法的数学模型 I,模拟列车在理想条件下的运行过程。然后,建立一个模型 II,通过调整运行时间来观察对应的速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线和能量消耗-距离曲线的变化。最后,将模型 I 和模型 II 的结果进行比较,分析不同条件下列车的运行情况和能耗差异。
问题二的分析
对问题 2 研究的意义的分析:问题 2 属于列车运行过程的数学建模问题。通过建立数学模型,以路况信息及复杂动态过程为问题一的约束条件,来获得列车可行的运行轨迹、牵引制动力、时间和能量消耗等曲线。这有助于了解列车在不同情况下的性能表现,为优化列车运行提供依据。对于解决此类问题一般数学方法的分析:针对列车运行过程中的速度、牵引制动力、时间和能量消耗等变化,我们可以使用粒子群优化算法来设计一条能耗最小的速度轨迹,并根据路况信息和列车动态特性进行相应的限制和调整,以达到行驶安全和经济的目的。
对题目中所给数据特点的分析:附件中给出了列车从XEQ 站到SMKXY站的路途中的坡度变化信息以及限速变化信息和电机的动态特性。其中,列车的质量和运行距离是确定的,而坡度信息决定速度上限、电机的恒转矩区和弱磁区则反映了列车加速度和减速度的范围;阻力则决定了列车运行过程中所受到的衰减力大小。
对问题 2 的题目要求进行分析:问题 2 要求通过建模方法编写程序,以获得列车在给定运行时间 T 下能耗最低的可行速度轨迹,并生成牵引制动力-距离曲线、时间-距离曲线和能量消耗-距离曲线,以及程序的运行时间。这些曲线可以用于描述列车在不同位置的运行状态和能耗情况,进而评估列车的性能和效率。此外,还需要获取列车以最短时间到达站台 B 的曲线,以及在最短运行时间上分别增加 10s、20s、50s、150s、300s 到达站台 B 总共六组曲线,以探索速度轨迹变化对列车能耗的影响。
为达成以上目标,我们首先需要在设计速度轨迹时,考虑列车的加速度和减速度限制,以保证列车的安全性和运行效率。同时,还需考虑列车行驶路段的坡度、阻力等因素,以优化能耗表现。然后,通过数值计算方法,可以对列车在不同速度下的能耗进行计算,并选择最小能耗的轨迹方案。最后,在得到初步的结果后,需要对速度轨迹进行进一步检验和优化,以满足列车的安全性和运行效率等要求。此外,还需根据题目要求获取列车在不同速度轨迹下到达站台 B 的曲线,以探索速度轨迹变化对列车能耗的影响。
模型假设:
1. 假设问题一中,站点之间的坡度为 0,列车做的是直线运动;
2. 假设牵引力和制动力产生的时间忽略不计,也即列车可在瞬间达到最大牵引力和最大制动力;
3. 忽略空气阻力和摩擦力;
4. 列车匀速运动时,F阻力 = F牵引力
5. 假设列车在某个固定长度的间隔内,所受的阻力恒定,阻力值为该间隔内初始速度的对应值。
论文缩略图:


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
列车加速阶段的求解模型:
import math
import pandas as pd
import time
start_time = time . time () # 记 录 代 码 开 始 时 间
# 列车质量
mass = 176300 # kg
# 列 车 加 速 度 阶 段 的 牵 引 力
traction_force = 33369 # N
# 列 车 速 度 上 限
velocity_limit = 27.8 # m / s
# 列 车 阻 力 公 式 参 数
k1 = 2.0895
k2 = 0.0098
k3 = 0.006
# 列 车 加 速 度 阶 段 的 数 量 ( 小段数 )
num_segments = 1000
# 列 车 站 点 间 的 总 距 离
total_distance = 5144.7 # m
# 列 车 在 每 个 小 段 内 的 长 度
segment_length = total_distance / num_segments # m
# 初始 化 变量
distance_traveled = 0
velocity = 0
elapsed_time = 0 # 修 改 变 量 名 为 elapsed_time
# 存 储 每 一 小 段 的 距 离 、 速度 、 时间
data = []
# 开 始 模 拟 列 车 运 动
for i in range ( num_segments ):
# 当 前 小 段 的 起 始 速 度
initial_velocity = velocity
# 计 算 当 前 小 段 内 的 阻 力
resistance = ( k1 + k2 * velocity + k3 * velocity ** 2) * 1000
# 计 算 当 前 小 段 内 的 加 速 度
acceleration = ( traction_force - resistance ) / mass
# 计 算 当 前 小 段 内 的 末 速 度
final_velocity = math . sqrt ( initial_velocity ** 2 + 2 * acceleration * segment_length )
t = ( final_velocity - initial_velocity ) / acceleration
# 如 果 末 速 度 超 过 速 度 上 限 , 则 以 速 度 上 限 为 准
if final_velocity > velocity_limit :
final_velocity = velocity_limit
# 更 新 列 车 的 距 离 和 速 度
distance_traveled += segment_length
velocity = final_velocity
# 累 加 时 间 并 将 其 添 加 到 列 表 中
elapsed_time += t
data . append ([ distance_traveled , velocity , elapsed_time ])
# 如 果 列 车 达 到 速 度 上 限 , 结 束 运 动 模 拟
if velocity >= velocity_limit :
break
# 将 数 据 转 换 为 DataFrame 格式
df = pd . DataFrame ( data , columns =[ 'Distance ', 'Velocity ', 'Time '])
# 获 取 时 间 的 累 加 值
df [' Time_cumsum '] = df ['Time ']. cumsum ()
# 将数 据 写入 Excel 表格中
df . to_excel ('p1 - aacc +10. xlsx ', sheet_name ='Sheet1 ', index = False )
print (" 列车 在 运行 %.2f 米 的 距 离 后 达 到 速 度 上 限 %.2 f m/s" % ( distance_traveled , velocity_limit ))
print (" 达 到 速 度 上 限 所 需 的 时 间 为 %.2f 秒" % elapsed_time )
end_time = time . time () # 记 录 代 码 结 束 时 间
execution_time = end_time - start_time # 计 算 代 码 运 行 时 间
print (" 代 码 运 行 时 间 为 %.2f 秒" % execution_time )
列车减速阶段的求解模型:
import math
import pandas as pd
# 列车质量
mass = 176300 # kg
# 列 车 初 始 速 度
initial_velocity = 27.8 # m / s
# 列 车 终 点 速 度
final_velocity = 0 # m / s
# 列车 制 动力
braking_force = 27629 # N
# 列 车 站 点 间 的 距 离
distance = 5144.7 # m
num_segments = 1000
# 每 个 小 段 的 长 度
segment_length = distance / 1000 # m
# 列 车 当 前 速 度
velocity = initial_velocity # m / s
# 列 车 运 行 距 离
total_distance = 0 # m
# 列 车 运 行 时 间
total_time = 0 # s
# 创建空的 DataFrame , 用 于 保 存 数 据
df = pd . DataFrame ( columns =[" 距离 (m)", " 速度 (m/s)", " 时间 (s)"])
# 逐 个 小 段 计 算 列 车 运 行 距 离 和 时 间 , 直 到 速 度 降 为 0
for i in range ( num_segments ):
# 当 前 小 段 开 始 速 度
segment_initial_velocity = velocity
# 计 算 当 前 小 段 的 阻 力
resistance = (2.0895 + 0.0098 * velocity + 0.006 * velocity ** 2) * 1000
# N
# 计 算 当 前 小 段 的 减 速 度
acceleration = ( braking_force + resistance ) / mass # m / s ^2
# # 计 算 当 前 小 段 内 的 末 速 度
# final_velocity = math . sqrt ( segment_initial_velocity ** 2 - 2 * acceleration * segment_length )
# 计 算 当 前 小 段 内 的 末 速 度
temp = segment_initial_velocity ** 2 - 2 * acceleration * segment_length
if temp < 0:
final_velocity = 0
else :
final_velocity = math . sqrt ( temp )
# 计 算 当 前 小 段 的 运 行 时 间
segment_time = ( velocity - final_velocity ) / acceleration # s
# 如 果 末 速 度 超 过 速 度 上 限 , 则 以 速 度 上 限 为 准
if final_velocity < 0:
final_velocity = 0
# # 计 算 当 前 小 段 的 运 行 距 离
# segment_distance = velocity * segment_time - 0.5 * acceleration * segment_time ** 2
# m
# 更 新 列 车 当 前 速 度
velocity -= acceleration * segment_time
# 更 新 列 车 总 运 行 距 离
total_distance += segment_length
# 更 新 列 车 总 运 行 时 间
total_time += segment_time
# 将 当 前 小 段 的 数 据 保 存 到 DataFrame 中
df . loc [ i ] = [ segment_length , velocity , segment_time ]
# 输 出 当 前 小 段 的 距 离 、 速 度 和时 间
print ("第 {} 小段 : 距离 {:.2 f} 米 , 速度 {:.2 f} 米/秒 , 时间 {:.2 f} 秒". format ( i +1 , segment_length , velocity , segment_time ))
# 如 果 速 度 已 经 降 为 0, 则 跳 出循 环
if final_velocity <= 0:
break
# 计 算 每 个 小 段 的 累 计 距 离 , 速 度和 时 间
df [" 总距离 (m)"] = df [" 距离 (m)"]. cumsum ()
df [" 总速度 (m/s)"] = df [" 速度 (m/s)"]. cumsum ()
df [" 总时间 (s)"] = df [" 时间 (s)"]. cumsum ()
# 将 DataFrame 保存到 Excel 文件中
filename = "p1 -de. xlsx "
with pd . ExcelWriter ( filename ) as writer :
df . to_excel ( writer , index = False )
# 输出结果
print (" 列车 在 运行 %.2 f 米 的 距 离 时 速 度 降 为 0。" % total_distance )
print (" 速度降为 0 时 所 需 的 时 间 为 %.2 f 秒 。" % total_time
列车速度运行轨迹的求解模型:
import math
distance = 5144.7 # 距离 , 单位为米
speed_limit = 100 # 速度上限 , 单位为 km / h
mass = 176.3 # 质量 , 单位为吨
inertia_factor = 1.08 # 旋 转 惯 量 因 子
max_traction_force = 310 # 最大 牵 引力 , 单位为 kN
max_brake_force = 760 # 最大 制 动力 , 单位为 kN
# 计算 Davis 阻力
def davis_friction ( v ):
v_ms = v / 3.6 # 将速度从 km / h 转换为 m / s
return 2.0895 + 0.0098* v_ms + 0.006* v_ms **2
# 计 算 列 车 受 到 的 总 阻 力
def total_friction ( v ):
return davis_friction ( v ) * mass * 9.8
# 计 算 列 车 加 速 度
def acceleration ( v ):
net_traction_force = max_traction_force - total_friction ( v )
return net_traction_force / mass
# 计 算 列 车 制 动 加 速 度
def brake_acceleration ( v ):
return max_brake_force / mass
# 计 算 列 车 能 耗
def energy_consumption (v , a ):
return total_friction ( v ) * v / 1000 + mass * ( inertia_factor /2) * ( a /(9.8*1000))**2 * distance
def Force ( final_velocity ):
traction_force = (310000 * 10) / final_velocity # 计 算 弱 磁 区 的 力
back_force = (760000 * 17) / final_velocity # 计 算 弱 磁 区 的 力
return traction_force , back_force
# 在 速 度 上 限 内 遍 历 所 有 速 度 , 找 到 最 小 的 能 耗 值 和 对 应 速 度
min_energy = math . inf
for v in range (1 , speed_limit + 1):
a = acceleration ( v )
energy = energy_consumption (v , a )
if energy < min_energy :
min_energy = energy
optimal_v = v
print (" The optimal speed is % dkm /h, and the minimum energy consumption is %.2 fkWh ." % ( optimal_v , min_energy ))