特征值和特征向量

本章特征值和特征向量的概念只在方阵的范畴内探讨。

相似矩阵

Grant：线性变换对应的矩阵依赖于所选择的基。

一般情况下，同一个线性变换在不同基下的矩阵不同。仍然以平面线性变换为例，Grant 选用标准坐标系下的基向量 $\mathbf{i},\mathbf{j}$ ，线性变换 $T$ 对应的矩阵为 $A$ ，而 Jennifer 使用另外一组基向量 ${\mathbf{i}}^{\prime },{\mathbf{j}}^{\prime }$ 。

我们已经知道矩阵 $A$ 是追踪基向量$\mathbf{i},\mathbf{j}$ 变换后的位置得到的，同样的线性变换在${\mathbf{i}}^{\prime },{\mathbf{j}}^{\prime }$ 下的表示，也需要追踪基向量 ${\mathbf{i}}^{\prime },{\mathbf{j}}^{\prime }$ 变换后的位置。具体过程如下：

对于 Jennifer 视角下的向量 $\mathbf{v}=\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]$

1. 同样的向量，用 Grant 的坐标系表示的坐标为 $P\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]$ ，其中$P$ 为基变换矩阵；
2. 用 Grant 的语言描述变换后的向量 $AP\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]$
3. 将变换后的结果变回 Jennifer 的坐标系 $P^{-1}AP\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]$

于是，我们得到同一个线性变换 $T$ 在 Jennifer 的坐标系下对应的矩阵为 $P^{-1}AP$ 。

这个结果暗示着数学上的转移作用，中间的矩阵 $A$ 代表 Grant 坐标系下所见到的变换，$P$ 和$P^{-1}$ 两个矩阵代表着转移作用(基变换矩阵)，也就是在不同坐标系之间进行转换，实际上也是视角上的转化。$P^{-1}AP$ 仍然代表同一个变换，只不过是从别的坐标系的角度来看。

下面给出严格的数学证明。在线性空间 $V$ 中取两组基，基变换公式为
$({\mathbf{b}}_1,{\mathbf{b}}_2,\cdots ,{\mathbf{b}}_n)=({\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n)P$ 。

设线性变换 $T$ 在这两组基下的矩阵分别为 $A$ 和 $B$ 。那么
$$\begin{gathered} T({\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n)=({\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n)A \\ T({\mathbf{b}}_1,{\mathbf{b}}_2,\cdots ,{\mathbf{b}}_n)=({\mathbf{b}}_1,{\mathbf{b}}_2,\cdots ,{\mathbf{b}}_n)B \end{gathered}$$
取向量 $\mathbf{v}\in V$ ，在两组基下的坐标向量分别为 $\mathbf{x},{\mathbf{x}}^{\prime }$，根据坐标变换公式有 $\mathbf{x}=P{\mathbf{x}}^{\prime }$
$$\begin{array}{rl}T(\mathbf{v})& =({\mathbf{b}}_1,{\mathbf{b}}_2,\cdots ,{\mathbf{b}}_n)B{\mathbf{x}}^{\prime }\\ & =({\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n)A\mathbf{x}\\ & =({\mathbf{b}}_1,{\mathbf{b}}_2,\cdots ,{\mathbf{b}}_n)P^{-1}AP{\mathbf{x}}^{\prime }\end{array}$$
因为 ${\mathbf{b}}_1,{\mathbf{b}}_2,\cdots ,{\mathbf{b}}_n$ 线性无关，所以
$$B=P^{-1}AP$$

因此， $B$ 和 $P^{-1}AP$ 表示同一种线性变换在不同基向量下的表示。

相似矩阵：设 $A,B$ 都是 $n$ 阶矩阵，若有 $n$ 阶可逆矩阵 $P$ ，使
$$B=P^{-1}AP$$
则称矩阵 $A$ 与 $B$ 相似(similar)，记作 $A\sim B$。

用初等行变换计算相似矩阵：计算相似矩阵 $P^{-1}AP$ 的一种有效方法是先计算 $AP$ ，然后用行变换将增广矩阵 $(P\mid AP)$ 化为 $(I\mid P^{-1}AP)$，这样就不需要单独计算$P^{-1}$了 。

特征值与特征向量

Grant：行列式告诉你一个变换对面积的缩放比例，特征向量则是在变换中保留在他所张成的空间中的向量，这两者都是暗含于空间中的性质，坐标系的选择并不会改变他们最根本的值。

我们已经知道，对角阵对于矩阵运算来说最为简单。若线性变换 $T$ 在一组基下的矩阵为 $A$，为便于应用，自然考虑是否存在对角阵 $\Lambda$ 和矩阵 $A$ 相似，从而使用这种最简单的形式计算线性变换。

假设有对角阵 $\Lambda \sim A$，即存在可逆矩阵 $P$ ，使得
$$P^{-1}AP=\Lambda =\text{diag}({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)$$
将矩阵 $P$ 按列分块 $P=({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_n)$ ，则上式等价于
$$A({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_n)=({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_n)\Lambda$$
按分块矩阵的乘法，上式可写成
$$\begin{gathered} A{\mathbf{x}}_1={\lambda }_1{\mathbf{x}}_1 \\ A{\mathbf{x}}_2={\lambda }_1{\mathbf{x}}_2 \\ \cdots \\ A{\mathbf{x}}_n={\lambda }_n{\mathbf{x}}_n \end{gathered}$$
根据假定 $P$ 可逆，其列向量非零，因此我们希望找到符合条件的 ${\lambda }_j,{\mathbf{x}}_j$。

定义：对于矩阵 $A$ ，如果存在数 $\lambda$ 和非零向量 $\mathbf{u}$，使得
$$A\mathbf{u}=\lambda \mathbf{u}$$

则称$\lambda$ 是矩阵 $A$ 的一个特征值（eigenvalue），$\mathbf{u}$ 是特征值 $\lambda$ 的一个特征向量（eigenvector）。

(1) 特征向量必须是非零向量；
(2) 特征值和特征向量是相伴出现的。

事实上，对于任意非零常数$c$， $c\mathbf{u}$ 都是特征值 $\lambda$ 的特征向量，这是因为
$$\text{if }A\mathbf{u}=\lambda \mathbf{u},\text{ then }A(c\mathbf{u})=\lambda (c\mathbf{u})$$
由于矩阵和线性变换是一一对应的，我们可以借助几何直观理解这个定义。

• 特征向量在变换过程中只受到拉伸或者压缩
• 特征值描述对应特征向量经过线性变换后的缩放程度

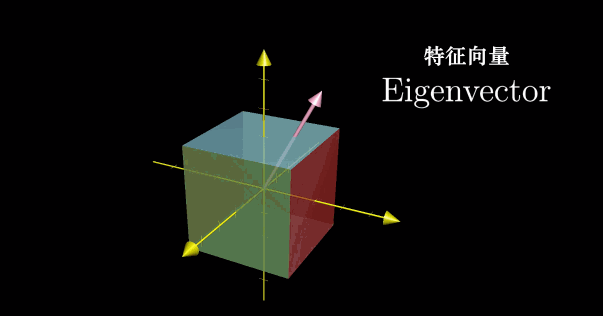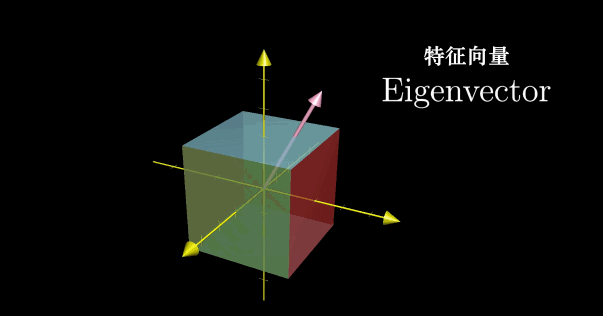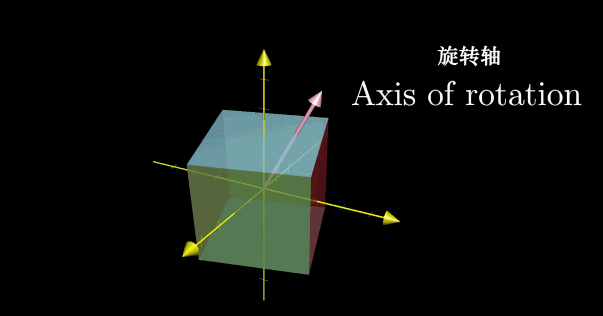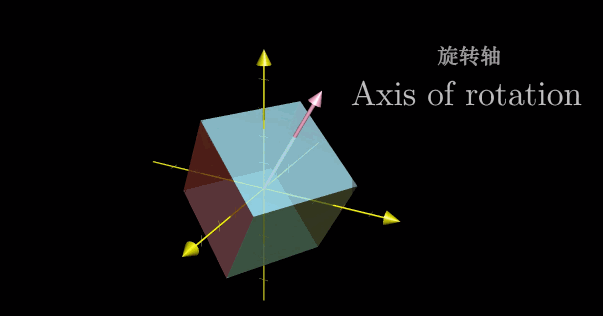
对于三维空间中的旋转，如果能够找到对应的特征向量，也即能够留在它所张成的空间中的向量，那么就意味着我们找到了旋转轴。特别地，这就意味着将一个三维旋转看成绕这个特征向量旋转一定角度，要比考虑相应的矩阵变换要直观。此时对应的特征值为1，因为旋转并不改变任何一个向量，所以向量的长度保持不变。

由定义知道，求解特征向量就是寻找非零向量 $\mathbf{u}$ 使得
$$(A-\lambda I)\mathbf{u}=0$$

显然，$\mathbf{u}=0$​ 时恒成立，但是我们要寻找的是非零解。 齐次矩阵方程有非零解的充分必要条件是系数矩阵的行列式为零，即
$$\det (A-\lambda I)=0$$
也就是系数矩阵所代表的线性变换将空间压缩到更低的维度。上式称为矩阵 $A$ 的特征方程(characteristic equation)。矩阵 $A$ 的特征值就是它的特征方程的根。

多项式
$$f(\lambda )=\det (A-\lambda I)$$
称为矩阵 $A$ 的特征多项式(characteristic polynomial)。

由上面的讨论可以得出求$n$阶矩阵$A$的特征值与特征向量的简要步骤：

1. 求出 $A$ 的特征多项式，即计算$n$阶行列式 $\det (A-\lambda I)$；
2. 求解特征方程 $\det (A-\lambda I)=0$ ，得到$n$个根，即为$A$的$n$ 个特征值；
3. 对求得的每个特征值 ${\lambda }_i$ 分别带入 $(A-\lambda I)\mathbf{x}=0$ 求其非零解，便是对应的特征向量。

示例：求矩阵 $A=\left[\begin{array}{cc}1& 2\\ 3& 2\end{array}\right]$ 的特征值和特征向量。

解： $A$ 的特征多项式为
$$\begin{array}{rl}\det (A-\lambda I)& =\left|\begin{array}{cc}1-\lambda & 2\\ 3& 2-\lambda \end{array}\right|\\ & ={\lambda }^2-3\lambda -4=(\lambda -4)(\lambda +1)\end{array}$$
因此 $A$ 的特征值为 ${\lambda }_1=4,{\lambda }_2=-1$。

将 ${\lambda }_1=4$ 带入矩阵方程 $(A-\lambda I)\mathbf{x}=0$ ，有
$$\begin{gathered} \left[\begin{array}{cc}-3& 2\\ 3& -2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=0 \\ \left[\begin{array}{cc}-3& 2\\ 3& -2\end{array}\right]\to \left[\begin{array}{cc}3& -2\\ 0& 0\end{array}\right] \end{gathered}$$
求得特征值 ${\lambda }_1=4$ 对应的一个特征向量 ${\mathbf{u}}_1=c\left[\begin{array}{c}2\\ 3\end{array}\right]$

将 ${\lambda }_1=-1$ 带入矩阵方程 $(A-\lambda I)\mathbf{x}=0$ ，有
$$\begin{gathered} \left[\begin{array}{cc}2& 2\\ 3& 3\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=0 \\ \left[\begin{array}{cc}2& 2\\ 3& 3\end{array}\right]\to \left[\begin{array}{cc}1& 1\\ 0& 0\end{array}\right] \end{gathered}$$
求得特征值 ${\lambda }_2=-1$ 对应的特征向量 ${\mathbf{u}}_2=c\left[\begin{array}{c}-1\\ 1\end{array}\right]$

性质：

1. 相似矩阵(同样的线性变换)有相同的特征多项式，从而有相同的特征值；
2. 矩阵 $A$ 与其转置矩阵 $A^T$ 有相同的特征值；
3. 属于矩阵不同特征值的特征向量线性无关；
4. 矩阵的所有特征值之和等于其主对角线元素之和(矩阵的迹)；
5. 矩阵的所有特征值之积等于矩阵的行列式；
6. 三角阵的特征值是其主对角线元素；
7. 矩阵乘积 $AB$ 和 $BA$ 具有相同的非零特征值

证明：(性质1)设 $A\sim B$，即 $B=P^{-1}AP$ ，于是
$$\begin{array}{rl}\det (B-\lambda I)& =\det (P^{-1}(A-\lambda I)P)\\ & =\det (P^{-1})\det (A-\lambda I)\det (P)\\ & =\det (A-\lambda I)\end{array}$$
故 $A$ 与 $B$ 有相同的特征多项式，从而有相同的特征值

(性质4)设$n$阶矩阵$A$ 的特征值为 ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$。由于矩阵的特征值就是其特征方程的根，从而
$$f(\lambda )=\det (A-\lambda I)=({\lambda }_1-\lambda )({\lambda }_2-\lambda )\cdots ({\lambda }_n-\lambda )$$
上式取 $\lambda =0$ ，有 $f(0)=\det A={\lambda }_1{\lambda }_2\cdots {\lambda }_n$

(性质7)假设矩阵 $A$ 与 $B$ 分别是 $m\times n$ 与 $n\times m$ 矩阵。

证法1：设 $\lambda$ 是 $AB$ 的任一非零特征值，$\mathbf{u}$ 是这一特征值的特征向量，则 $(AB)\mathbf{u}=\lambda \mathbf{u}$ ，等式两边同时左乘 $B$ 有

$$(BA)(B\mathbf{u})=\lambda (B\mathbf{u})$$

又由于 $AB\mathbf{u}=\lambda \mathbf{u}\ne 0$ 可知 $B\mathbf{u}\ne 0$ 。所以 $B\mathbf{u}$ 是 $BA$ 关于特征值 $\lambda$ 的特征向量。这也证明了$\lambda$ 也是$BA$ 的特征值。

同理可证 $BA$ 的非零特征值也是$AB$ 的特征值。这就证明了$AB$ 和 $BA$ 具有相同的非零特征值。

证法2：易知
$$\left[\begin{array}{cc}{I}_m& -A\\ O& I_n\end{array}\right]\left[\begin{array}{cc}AB& O\\ B& O\end{array}\right]\left[\begin{array}{cc}{I}_m& A\\ O& I_n\end{array}\right]=\left[\begin{array}{cc}O& O\\ B& AB\end{array}\right]$$

又由于
$$\left[\begin{array}{cc}{I}_m& -A\\ O& I_n\end{array}\right]\left[\begin{array}{cc}{I}_m& A\\ O& I_n\end{array}\right]=I_{m+n}$$

可知
$$\left[\begin{array}{cc}AB& O\\ B& O\end{array}\right]\sim \left[\begin{array}{cc}O& O\\ B& BA\end{array}\right]$$

它们有相同的特征多项式，即
$${\lambda }^n\det (\lambda I_m-AB)={\lambda }^m\det (\lambda I_n-BA)$$

上式称为Sylvester降幂公式。这里表明，$AB$ 和 $BA$ 的只相差了个 $m-n$ 个零特征值，其余非零特征值相同。

特征基与对角化

由上节知道，特征值和特征向量定义的初衷是为了线性变换的相似对角化，即
$$P^{-1}AP=\Lambda$$
由定义的推理知道，矩阵 $A$ 的每个特征向量就是 $P$ 的一个列向量，而 $P$ 是矩阵 $A$ 的基向量到对角阵 $\Lambda$ 基向量的过渡矩阵。过渡矩阵 $P$ 也可看作对角阵 $\Lambda$ 的基向量组在矩阵 $A$ 基向量下的坐标，所以对基向量的限制条件也适用于特征向量组。

定理：矩阵 $A_n$ 可以相似对角化的充要条件是 $A_n$ 有 $n$ 个线性无关的特征向量。此时，对角元素就是对应的特征值。

设矩阵$A$的特征值与特征向量对应关系 $A{\mathbf{u}}_1={\lambda }_1{\mathbf{u}}_1,A{\mathbf{u}}_2={\lambda }_2{\mathbf{u}}_2$ ，令$P=[{\mathbf{u}}_1,{\mathbf{u}}_2]$
$$AP=[{\lambda }_1{\mathbf{u}}_1,{\lambda }_2{\mathbf{u}}_2]=[{\mathbf{u}}_1,{\mathbf{u}}_2]\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]=P\Lambda$$

若 $P$ 可逆，即 ${\mathbf{u}}_1,{\mathbf{u}}_2$ 线性无关，则
$$\Lambda =P^{-1}AP=\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]$$

当特征向量的数量足够多时，这些特征向量就可以构成特征基(eigenbasis)。在特征基坐标系角度看，同一个线性变换只是伸缩变换(对角阵)。

特征基的坐标使用的是矩阵 $A$ 的基向量。

例：尝试将下列矩阵对角化
$$A=\left[\begin{array}{ccc}1& 3& 3\\ -3& -5& -3\\ 3& 3& 1\end{array}\right]$$
解：对角化工作可分为4步来完成

step 1：求出特征值。矩阵 $A$ 的特征方程为
$$\det (A-\lambda I)=-(\lambda -1)(\lambda +2{)}^2$$
特征值是 $\lambda =1$ 和 $\lambda =-2$

step 2：求出线性无关的特征向量。对于 $\lambda =1$ 的特征向量 ${\mathbf{u}}_1=(1,-1,1{)}^T$

对于 $\lambda =-2$ 的特征向量 ${\mathbf{u}}_2=(-1,1,0{)}^T$ 和 ${\mathbf{u}}_3=(-1,0,1{)}^T$

可以验证 ${\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3$ 是线性无关的。

step 3：使用特征向量构造过渡矩阵(向量的次序不重要)
$$P=\left[\begin{array}{ccc}1& -1& -1\\ -1& 1& 0\\ 1& 0& 1\end{array}\right]$$
step 4：使用对应的特征值构造对角阵(特征值的次序必须和矩阵$P$的列选择的特征向量的次序一致)
$$\Lambda =\left[\begin{array}{ccc}1& 0& 0\\ 0& -2& 0\\ 0& 0& -2\end{array}\right]$$
可简单验证 $AP=P\Lambda$，这等价于验证当 $P$ 可逆时 $\Lambda =P^{-1}AP$ 。

一些常见变换的特征值与特征向量列举如下：

(1) 等比例缩放变换 $\left[\begin{array}{cc}k& 0\\ 0& k\end{array}\right]$ 的特征多项式为 $(\lambda -k{)}^2$ ，有两个相等的特征值 $\lambda =k$ ，但平面内任意非零向量都属于这个特征值的特征向量。

(2) 普通缩放变换 $\left[\begin{array}{cc}{k}_1& 0\\ 0& k_2\end{array}\right]$ 的特征多项式为 $(\lambda -k_1)(\lambda -k_2)$ ，有两个特征值 ${\lambda }_1=k_1,{\lambda }_2=k_2$ ，特征向量分别为 ${\mathbf{u}}_1=\left[\begin{array}{c}1\\ 0\end{array}\right],{\mathbf{u}}_2=\left[\begin{array}{c}0\\ 1\end{array}\right]$。

(3) 旋转变换 $\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$ 的特征多项式为 ${\lambda }^2+2\lambda \cos \theta +1$ ，有两个复特征值 ${\lambda }_1=\cos \theta +i\sin \theta ,{\lambda }_2=\cos \theta -i\sin \theta$ ，对应两个复特征向量 ${\mathbf{u}}_1=\left[\begin{array}{c}1\\ -i\end{array}\right],{\mathbf{u}}_2=\left[\begin{array}{c}1\\ i\end{array}\right]$。

值得注意的是，特征值出现虚数的情况一般对应于变换中的某一种旋转。

(4) 水平剪切变换 $\left[\begin{array}{cc}1& k\\ 0& 1\end{array}\right]$ 的特征多项式为 $(\lambda -1{)}^2$ ，有两个相等的特征值 $\lambda =1$ ，只有一个特征向量 ${\mathbf{u}}_1=\left[\begin{array}{c}1\\ 0\end{array}\right]$ ，不能张成整个平面。

特征向量的应用

许多实际问题都可归结为研究矩阵的方幂 $A^n(n\in {\mathbb{N}}^{\ast })$ 乘以向量 $\mathbf{v}$ ，不难想象，当方幂很大时，直接用矩阵的乘法、矩阵与向量的乘法进行计算会非常麻烦。而矩阵的特征值和特征向量矩阵对幂运算十分友好，因此在数学和实际问题中有着广泛的应用。

性质：

1. 设矩阵 $A$ 特征值 $\lambda$ 的特征向量为 $\mathbf{u}$，则用数学归纳法可以得到
   $$A^n\mathbf{u}={\lambda }^n\mathbf{u}$$

2. 设矩阵 $A$ 特征值 ${\lambda }_1,{\lambda }_2$ 的特征向量分别为 ${\mathbf{u}}_1,{\mathbf{u}}_2$。对于任意向量 $\mathbf{v}$ ，可以用特征向量线性表示 $\mathbf{v}=v_1{\mathbf{u}}_1+v_2{\mathbf{u}}_2$ 。那么，用数学归纳法可以得到
   $$A^n\mathbf{v}=v_1{\lambda }_1^n{\mathbf{u}}_1+v_2{\lambda }_2^n{\mathbf{u}}_2$$

证明：从线性变换的角度理解，性质1中矩阵 $A$ 只是对特征向量做伸缩变换，因此矩阵幂的效果等价于特征值(缩放比例)的幂。性质2中矩阵的幂变换等同于切换到特征基中做了同等次数的伸缩变换。

性质1用数学归纳法证明：
(1) 当 $n=1$ 时
$$A\mathbf{u}=\lambda \mathbf{u}$$
(2) 假设当 $n=k-1$ 时成立，即
$$A^{k-1}\mathbf{u}={\lambda }^{k-1}\mathbf{u}$$
当 $n=k$ 时，因为
$$A^k\mathbf{u}=A(A^{k-1}\mathbf{u})=A({\lambda }^{k-1}\mathbf{u})={\lambda }^{k-1}(A\mathbf{u})={\lambda }^k\mathbf{u}$$

所以，对 $n=k$ 时成立。由数学归纳法可知，对所有的 $n\in {\mathbb{N}}^{\ast }$ 都成立。

实例：在扩散理论中的应用。设某物质能以气态和液态的混合状态存在，假定在任意一段很短的时间内
(1) 液体的 $5\%$ 蒸发成气态；
(2) 气体的 $1\%$ 凝结成液态。
假定该物质的总量一直保持不变，那么最终的情况如何？

为了研究的方便，用 $g_0,l_0$ 分别表示现在的气体和液体的比例 $(g_0+l_0=1)$， $g_n,l_n$ 分别表示 $n$ 段时间后液体和气体的比例。记物质总量为 $M$ ，一直保持不变。

(1) 先求 $g_1,l_1$

可以看出，在很短时间后，气体由现在气体的 $99\%$ 加上现在液体的 $5\%$ 组成，即
$$g_{1}M=0.99g_{0}M+0.05l_{0}M$$
同理，在很短时间后的液体
$$l_{1}M=0.01g_{0}M+0.95l_{0}M$$
因此
$$\{\begin{array}{l}{g}_1=0.99g_0+0.05l_0\\ l_1=0.01g_0+0.95l_0\end{array}$$
矩阵形式为
$$\left[\begin{array}{c}{g}_1\\ l_1\end{array}\right]=\left[\begin{array}{cc}0.99& 0.05\\ 0.01& 0.95\end{array}\right]\left[\begin{array}{c}{g}_0\\ l_0\end{array}\right]$$
记矩阵$P=\left[\begin{array}{cc}0.99& 0.05\\ 0.01& 0.95\end{array}\right]$ 则上式写为
$$\left[\begin{array}{c}{g}_1\\ l_1\end{array}\right]=P\left[\begin{array}{c}{g}_0\\ l_0\end{array}\right]$$
矩阵 $P$ 记录了很短时间内气液的转变情况。

(2) 类似与 $g_1,l_1$ 的推导过程，可以得到
$$\begin{array}{rl}& \left[\begin{array}{c}{g}_1\\ l_1\end{array}\right]=P\left[\begin{array}{c}{g}_0\\ l_0\end{array}\right];\\ & \left[\begin{array}{c}{g}_2\\ l_2\end{array}\right]=P\left[\begin{array}{c}{g}_1\\ l_1\end{array}\right]=P^2\left[\begin{array}{c}{g}_0\\ l_0\end{array}\right];\\ & \cdots \cdots \\ & \left[\begin{array}{c}{g}_n\\ l_n\end{array}\right]=P\left[\begin{array}{c}{g}_{n-1}\\ l_{n-1}\end{array}\right]=P^n\left[\begin{array}{c}{g}_0\\ l_0\end{array}\right]\end{array}$$
由于该问题已转化为矩阵指数的形式，我们可以用矩阵特征值和特征向量的性质求解。

(3) 可以证明矩阵
$$A=\left[\begin{array}{cc}1-p& q\\ p& 1-q\end{array}\right](0<p,q<1)$$
的特征值是 ${\lambda }_1=1,{\lambda }_2=1-p-q$，对应的特征向量分别是 ${\mathbf{u}}_1=\left[\begin{array}{c}q\\ p\end{array}\right],{\mathbf{u}}_2=\left[\begin{array}{c}1\\ -1\end{array}\right]$。

从而得到矩阵 $P$ 的特征值是 ${\lambda }_1=1,{\lambda }_2=0.94$，对应的特征向量分别是 ${\mathbf{u}}_1=\left[\begin{array}{c}0.05\\ 0.01\end{array}\right],{\mathbf{u}}_2=\left[\begin{array}{c}1\\ -1\end{array}\right]$。再把初始向量 $\left[\begin{array}{c}{g}_0\\ l_0\end{array}\right]$ 用特征向量表示，设
$$\left[\begin{array}{c}{g}_0\\ l_0\end{array}\right]=k_1\left[\begin{array}{c}0.05\\ 0.01\end{array}\right]+k_2\left[\begin{array}{c}1\\ -1\end{array}\right]\text{where }{g}_0+l_0=1$$
解得 $k_1=\frac{50}{3},k_2=g_0-\frac{5}{6}$ ，所以由性质2得，对于任意的自然数 $n$ 有
$$\left[\begin{array}{c}{g}_n\\ l_n\end{array}\right]=P^n\left[\begin{array}{c}{g}_0\\ l_0\end{array}\right]=k_1\times 1^n\left[\begin{array}{c}0.05\\ 0.01\end{array}\right]+k_2\times 0.94^n\left[\begin{array}{c}1\\ -1\end{array}\right]$$
从而 $g_n=0.05k_1+0.94^n{k}_2,l_n=0.01k_1-0.94^n{k}_2$，所以
$$\begin{gathered} g_{\infty }=\underset{n\to \infty }{\lim }(0.05k_1+0.94^n{k}_2)=0.05k_1=\frac{5}{6} \\ {l}_{\infty }=\underset{n\to \infty }{\lim }(0.01k_1-0.94^n{k}_2)=0.01k_1=\frac{1}{6} \end{gathered}$$
那么，我们可以得到，不管该物质最初的气液比率如何，最终将达到一个平衡状态，此时该物质的 $5/6$ 是气态的，$1/6$ 是液体的。