（1）455分发饼干–简单

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {//升序排序sort(g.begin(), g.end());sort(s.begin(), s.end());int cookie = 0;int child = 0;//贪心算法，尽可能用小饼干满足更多孩子while(cookie < s.size() && child < g.size()){if(g[child] <= s[cookie]){//该孩子满足了，满足下一个孩子child++;}//如果未满足，则当前饼干一定不能满足剩下的孩子，移动到下一块//如果满足，则当前饼干被消耗，移动到下一块cookie++;}return child;}
};

（2）376摆动序列–中等

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。


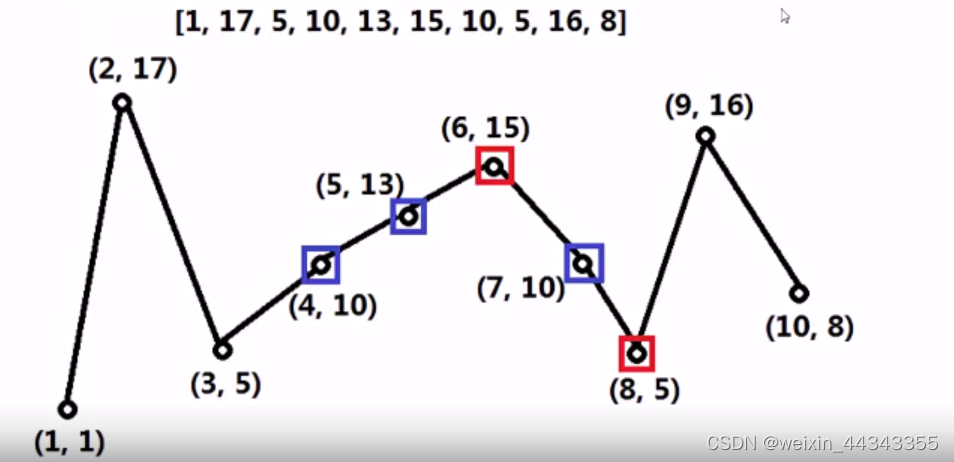
连续递增或递减时，选择红色点

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if(nums.size()==0) return 0;if(nums.size()==1) return 1;//利用状态机转换//三个状态static const int begin = 0;static const int up = 1;static const int down = 2;int STATE = begin;int maxLength = 1;//初始长度为1for(int i = 1; i< nums.size(); i++){switch(STATE){//当状态为begin时case begin:if(nums[i]>nums[i-1]){STATE = up;maxLength++;}else if(nums[i] < nums[i-1]){STATE = down;maxLength++;}//如果两数相等，不发生状态转换break;case up:if(nums[i] < nums[i-1]){STATE = down;maxLength ++;}//如果两数相等或后一个大于前一个，不发生状态转换break;case down:if(nums[i] > nums[i-1]){STATE = up;maxLength ++;}//如果两数相等或后一个小于前一个，不发生状态转换break;}}return maxLength;}
};

（3）402移调k位数–中等

给你一个以字符串表示的非负整数 num 和一个整数 k ，移除这个数中的 k 位数字，使得剩下的数字最小。请你以字符串形式返回这个最小的数字。

#include<string>
using namespace std;
class Solution {
public:string removeKdigits(string num, int k) {if(k >= num.size()) return "0";vector<int> S;string result = "";int number;for(int i = 0; i< num.length(); i++){//从高位开始，保留尽可能小的数number = num[i] - '0';//字符串转换为数字，0要用单引号，表示一个字符，双引号表示一个字符串while(S.size()> 0 && number < S[S.size() - 1] && k>0){//if(S.size() == 1 && number == 0) break;//如果栈中只有一个元素，且新来的元素是0，不能用0替换栈顶S.pop_back();//如果新元素比栈顶小，就保留新元素k--;}//0不能作为开头元素if(number != 0 || S.size() != 0 ){S.push_back(number);}}if(S.size() == 0 || k >= S.size()) return "0";//如果序列都遍历完而k还未用完时，得到的栈中元素一定是单调递增的。while(k > 0) {S.pop_back();k--;}if(S.size() == 0) return "0";for(int i = 0; i< S.size(); i++){//char tmp = S[i]+'0';//result = result+ tmp;//这样转字符，超长用例会报超时，不知道为啥result.append(1,S[i]+'0');//在当前字符串结尾添加1个字符}return result;}
};

append函数的用法参考：https://blog.csdn.net/weixin_42258743/article/details/107964192

（4）55跳跃游戏

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

法一：

class Solution {
public:bool canJump(vector<int>& nums) {//关键在于如何选择下一条的节点//下一跳能跳的越远越有利，因此选择能达到最远的节点if(nums.size()== 1) return true;int next_index = -1;int index = 0;int max_distance = 0;//此处赋值为负数的话会导致与size函数返回值（无符号数）比较出错while((index+max_distance <= (nums.size()-1)) && (next_index != index)){//下一跳等于当前下标，则证明不能到达//下一条等于大于总长度，则证明可到达max_distance = 0;//index更新至下一跳处if (next_index != -1) index = next_index;//cout<<"index = "<< index << " next_index = "<<next_index<<endl;if(nums[index] == 0) break;else{for(int i = 1; i<= nums[index] && (i+index<nums.size()); i++){//遍历从index到index+nums[i]能到达的所有元素，找出最远距离if((i+nums[i+index]) > max_distance){max_distance = (i+nums[i+index]);next_index = index+i;//cout<< " i="<<i<<" max_distance=" << max_distance<<endl;}}}//cout<<"index = "<< index << " next_index = "<<next_index<<endl;}if((index+max_distance >= (nums.size()-1)) ) return true;return false;}
};

法二：

class Solution {
public:bool canJump(vector<int>& nums) {if(nums.size() == 1) return true;int length = nums.size();//总长度int tmp = nums[0];//tmp记录当前能到达的最远距离int i = 1;for(i; (i< length && tmp > 0); i++){tmp--;cout<< "tmp="<<tmp<<" nums[" << i<<"]=" << nums[i]<< " ";//如果当前节点能到达的距离比之前的远，tmp更新为当前节点的值if(nums[i] > tmp){ tmp = nums[i];}//cout<< tmp << "picked"<<endl;}//cout<< "tmp="<<tmp<<endl;if(i >= length && tmp >= 0) return true;return false;}
};

（5）45跳跃游戏二–中等

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

此题根据跳跃游戏的 法一 改编得到
https://blog.csdn.net/weixin_44343355/article/details/128772719

class Solution {
public:int jump(vector<int>& nums) {//关键在于如何选择下一条的节点//下一跳能跳的越远越有利，因此选择能达到最远的节点if(nums.size() < 2) return 0;int next_index = 0;int index = 0;int max_distance = nums[0];//此处赋值为负数的话会导致与size函数返回值（无符号数）比较出错int jump_times = 0;int length = nums.size();while(((max_distance) < length -1)){//最远能到的距离等于大于总长度，则证明可到达for(int i = 1; i<= nums[index] && (i+index<nums.size()); i++){//遍历从index到index+nums[i]能到达的所有元素，找出最远距离if((i+nums[i+index]+index) > max_distance){max_distance = (i+nums[i+index]+index);next_index = index+i;//cout<< " i="<<i<<" max_distance=" << max_distance<<endl;}}index = next_index;jump_times++;}return jump_times+1;}
};

（6）452用最少数量的箭引爆气球–中等

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

//注意，此处需要加引用
bool cmp(const vector<int> &a, const vector<int> &b){return a[0] < b[0];
}class Solution {
public:int findMinArrowShots(vector<vector<int>>& points) {if(points.size() == 1) return 1;sort(points.begin(), points.end(), cmp);//按左端点从小到大升序排序int length = points.size();int shootNum = 1;int shooter_begin = points[0][0];int shooter_end = points[0][1];for(int i = 1;i<length;i++){//如果新节点的左端点在shooter的范围内，则说明两区间有重合部分，需要一箭即可射穿if(points[i][0] >= shooter_begin && points[i][0] <= shooter_end){//更新shooter的左端点shooter_begin = points[i][0];//如果shooter的右端点大于新节点的右端点，则更新右端点if(points[i][1] <= shooter_end){shooter_end = points[i][1];}}//如果无交集，则新选择一个射手else{shootNum++;shooter_begin = points[i][0];shooter_end = points[i][1];}}return shootNum;}
};

（7）871最低加油次数–困难

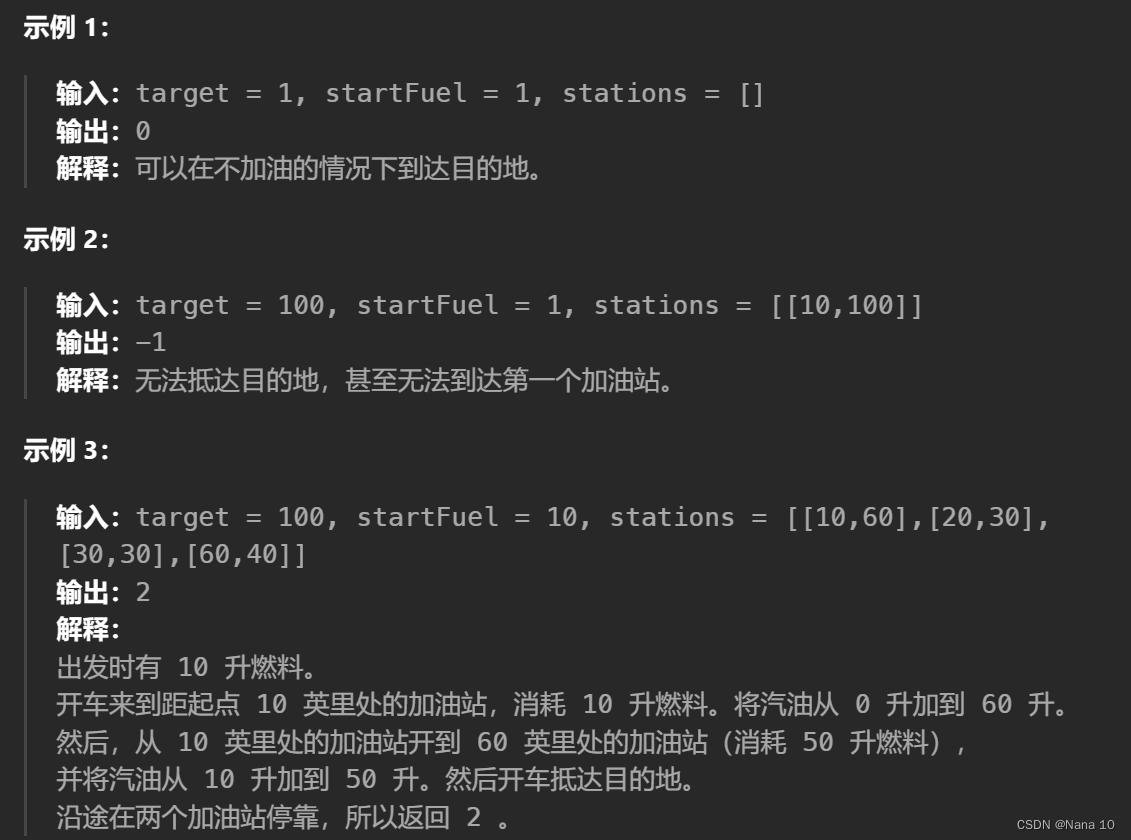
汽车从起点出发驶向目的地，该目的地位于出发位置东面 target 英里处。

沿途有加油站，用数组 stations 表示。其中 stations[i] = [positioni, fueli] 表示第 i 个加油站位于出发位置东面 positioni 英里处，并且有 fueli 升汽油。

假设汽车油箱的容量是无限的，其中最初有 startFuel 升燃料。它每行驶 1 英里就会用掉 1 升汽油。当汽车到达加油站时，它可能停下来加油，将所有汽油从加油站转移到汽车中。

为了到达目的地，汽车所必要的最低加油次数是多少？如果无法到达目的地，则返回 -1 。

注意：如果汽车到达加油站时剩余燃料为 0，它仍然可以在那里加油。如果汽车到达目的地时剩余燃料为 0，仍然认为它已经到达目的地。

此题的思路与跳跃游戏二中的思路类似，都是求最小跳跃次数，用贪心的思想

class Solution {
public:int minRefuelStops(int target, int startFuel, vector<vector<int>>& stations) {if(stations.size() == 0){if(target > startFuel) return -1;else return 0;}// if(stations.size() == 1){//     if(target < startFuel) return 0;//     else if(stations[0][0] > startFuel || (stations[0][1]+startFuel) < target) return -1;//     else return 1;// }int leftFuel = startFuel;//剩余油量priority_queue<int, vector<int>, less<int>> maxFuel;//途中站点的最大油量,加过油的站点就不能再加油了，所以用 堆来存储，依次输出最大站点int addFuelTimes = 0;//加油次数int i = 0;int maxfuel = 0;vector<int> target_vector;target_vector.push_back(target);target_vector.push_back(0);stations.push_back(target_vector);for(i = 0; i< stations.size(); i++){//cout<< "i="<<i<<" ";leftFuel = startFuel - stations[i][0];//剩余油量//剩余油量小于等于0，则表明过程中需要加一次油//无法到达该点，先加油while(leftFuel < 0 && maxFuel.size()>0){maxfuel = maxFuel.top();maxFuel.pop();leftFuel = leftFuel + maxfuel;startFuel = startFuel +maxfuel;addFuelTimes ++;}if(leftFuel<0) return -1;maxFuel.push(stations[i][1]);//前面所有站点的油都加完了，如果还到不了该点，返回无法到达//cout<<endl;}return addFuelTimes;}};