2023年华数杯全国大学生数学建模
A题 隔热材料的结构优化控制研究
原题再现:
新型隔热材料 A 具有优良的隔热特性,在航天、军工、石化、建筑、交通等高科技领域中有着广泛的应用。
目前,由单根隔热材料 A 纤维编织成的织物,其热导率可以直接测出;但是单根隔热材料 A 纤维的热导率(本题实验环境下可假定其为定值),因其直径过小,长径比(长度与直径的比值)较大,无法直接测量。单根纤维导热性能是织物导热性能的基础,也是建立基于纤维的各种织物导热模型的基础。建立一个单根隔热材料 A 纤维的热导率与织物整体热导率的传热机理模型成为研究重点。该模型不仅能得到单根隔热材料 A 纤维的热导率,解决当前单根 A 纤维热导率无法测量的技术难题;而且在建立的单根隔热材料 A 纤维热导率与织物热导率的关系模型的基础上,调控织物的编织结构,进行优化设计,能制作出更好的满足在航天、军工、石化、建筑、交通等高科技领域需求的优异隔热性能织物。
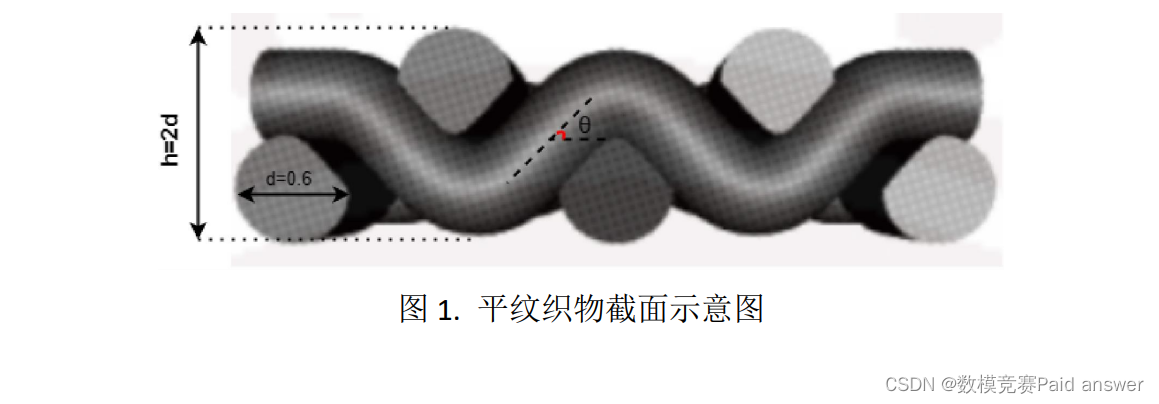
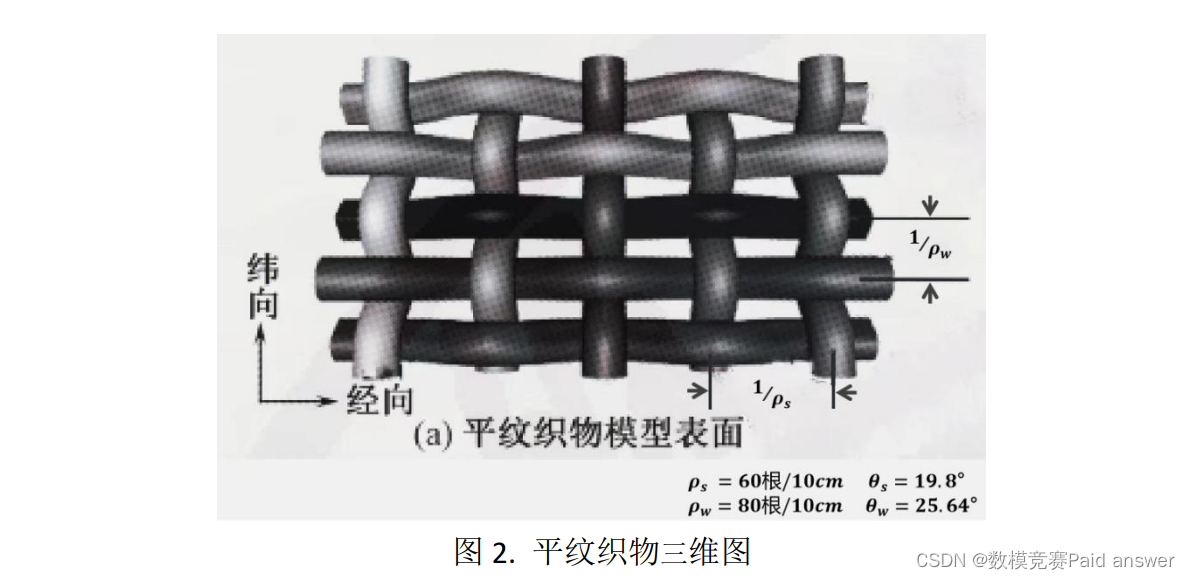
织物是由大量单根纤维堆叠交织在一起形成的网状结构,本题只研究平纹织物,如图 1 和图 2 所示。不同直径纤维制成的织物,其基础结构参数不同,即纤维弯曲角度、织物厚度、经密、纬密等不同,从而影响织物的导热性能。本题,假设任意单根 A 纤维的垂直切面为圆形,织物中每根纤维始终为一个有弯曲的圆柱。经纱、纬纱弯曲角度 10° < θ ≤ 26.565°。
热导率是纤维和织物物理性质中最重要的指标之一。织物的纤维之间存在空隙,空隙里空气为静态空气,静态空气热导率 0.0296 W/(mK)。计算织物热导率时既考虑纤维之间的传热,也不能忽略空隙中空气的传热。
我们在 25℃实验室环境下,用 Hotdisk 装置对织物进行加热和测量,Hotdisk恒定功率为 1mW,作用时间 1s,在 0.1s 时热流恰好传递到织物另一侧。实验测得 0~0.1s 之间织物位于热源一侧的温度随时间变化的数据见附件 1。
请建立数学模型,回答下列问题:
问题 1:假设附件 1 的温度为热源侧织物的表面温度,只考虑纤维传热和空隙间的气体传热,建立平纹织物整体热导率与单根纤维热导率之间关系的数学模型。在附件 2 的实验样品参数条件下,测得如图 2 所示的平纹织物的整体热导率为 0.033W/(mK),请根据建立的数学模型计算出单根 A 纤维的热导率。
问题 2:假设:1)制成织物的任意单根 A 纤维的直径在 0.3mm~0.6mm。2)织物位于热源一侧表面温度随时间的变化的数据依旧参考附件 1。3)由于温度和织物结构造成的织物整体密度和比热的变化可以忽略。请问如何选用单根 A纤维的直径及调整织物的经密、纬密、弯曲角度,使得织物的整体热导率最低。
问题 3:如果附件 1 的温度实际是热源侧织物表面空气的温度,此时该侧就会发生对流换热,假定织物表面的对流换热系数为 50 W/(m2K),请重新解答问题一和问题二。
整体求解过程概述(摘要)
随着科技的发展,新型隔热材料 A 在许多高科技领域中发挥着越来越重要的作用。热导率是衡量纤维和织物的物理性质的最重要指标之一,但目前由于织物的纤维之间存在着空气间隙,因此仅能测出由 A 纤维编制物编制而成的织物整体的热导率,而无法得到单根纤维的热导率。
本题旨在研究如何通过建立数学模型来求得该隔热材料制成的织物整体与单根织物之间的热导率关系,根据其热导率关系和测得的织物整体热导率来推算织物单根的热导率。研究纤维弯曲角度、织物厚度、经密和纬密等对织物导热性能的影响。
针对问题一:根据题目给出的单根纤维直径、织物整体的长、宽、纤维数量、弯曲角度和静态空气热导率来求解出纤维的体积分数,建立织物整体与单根纤维热导率之间的关系数学模型,再利用热传导方程和中心差分方程求出织物整体导热系数,最后根据建立的织物整体与单根热导率之间的关系数学模型来求解出单根纤维的热导率为:0.0392W/(𝑚k)。
针对问题二:基于问题一建立的模型,根据题目中给出的纤维直径和角度的变化范围,代入优化数学模型后求得在不同纤维直径、角度、经密、纬密时的单根纤维热导率,找出整体最小的热导率为:0.0297w/(𝑚k),再找出对应的纤维经向直径为:0.0311cm,纬向直径为:0.0311cm,经向角度为:11.8417°纬向角度为:16.7309°,经密为:4.1 根/cm,纬密为:4.2 根/cm。
针对问题三:在问题一和二所建立的模型的基础上,考虑热源侧的对流换热现象后,找出织物表面的温度分布后得出在此条件下的热传导方程,再对热传导方程进行求解,得出织物整体与单根纤维的热导率关系并计算出单根纤维的热导率。再对此模型进行优化,得出织物整体最小的热导率后计算出纤维直径、经密、纬密、弯曲角度等。
模型假设:
结合本题实际情况并综合分析后,为了避免一些不必要或者相对影响较小的因素对模型的准确性和和理性的干扰,故提出以下几点假设:
1.假设单根隔热材料A 纤维的热导率为固定值;
2.假设任意单根A 纤维的垂直切面为圆形;
3.假设制成织物的任意单根A 纤维的直径在0.3mm~0.6mm之间;
4.织物位于热源一侧表面温度随时间的变化的数据参考附件 1;
5.假设织物整体密度和比热的变化忽略不计;
6.假设单根纤维的总长度一致;
7.假设织物表面的对流换热系数为 50w/(𝑚k)。
问题分析:
问题一的分析
问题一要求解找出织物整体的热导率与单根纤维的热导率之间的关系模型。由附件1 热源侧织物的表面温度可算出织物整体热导率;由于题中已给出单根纤维的直径、织物整体的长和宽、纤维总根数、纤维的弯曲角度和静态空气的热导率。可以根据这些已知条件,求出纤维的体积分数。可以根据纤维的体积分数、静态空气的热导率,得到织物整体热导率和单根纤维热导率的关系。通过该关系式求出平纹织物的整体热导率为0.033w/(𝑚k)时的单根纤维热导率。
问题二的分析
问题二要求解得到使得整体热导率最低时的单根纤维直径及经密、纬密、弯曲角度。基于问题1得出的数学模型,以及问题2中给出的纤维直径,以及角度的变化范围,通过织物整体与单根纤维的热导率关系,改变单根纤维的直径及经密、纬密、弯曲角度,可得出织物整体热导率与单根直径,纬纱弯曲角度,经纱弯曲角度,单根热导率的关系。求得每一种情况的热导率,再找出最小热导率所对应的纤维直径及经密、纬密、弯曲角度。最后得出最优单根纤维直径,弯曲角度,以及密度。
问题三的分析
问题 3 要求考虑热源测发生对流换热的情况下,假定织物表面对流换热系数为50W/(m²K),找出织物整体的热导率与单根纤维的热导率之间的关系模型和单根纤维热导率,并且得到整体热导率最低时的单根纤维直径及经密、纬密、弯曲角度。先将附件1 给出的空气温度随时间变化,拟合后建立对流换热后热源侧温度的传导方程,计算出整体热导率与单根热导率的关系后,重新计算问题1中单根纤维的热导率,以及问题2中的单根纤维热导率,以及最优单根纤维直径、弯曲角度和密度等。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:
clc;
clear;
d=0.06;
k1=60;%经
k2=80;%纬
L_zong=10;%单位 cm
L_danh=(L_zong-d)/(k1-1);
L_danz=(L_zong-d)/(k2-1);
%角度
jiao1=19.8;
jiao2=25.64;
rad1=jiao1*pi/180;
rad2=jiao2*pi/180;
%单位内单根长度
L_zongh=(L_danh/cos(rad1))*(k1-1);%横向
L_zongz=(L_danz/cos(rad2))*(k2-1);%纵向
%单根纤维底面积
S_d=d/2*d/2*pi;
%单根体积
V_hdan=L_zongh*S_d; %横向
V_zdan=L_zongz*S_d; %纵向
%总体积
V_zongh=V_hdan.*k2; %横向
V_zongz=V_zdan.*k1; %纵向
%整体体积
V_fang=2*d*10*10;
V_zong=[];
V_tifen=[];
k_xian=0.033;
k_air=0.0296;
V_zong=V_zongz+V_zongh;
V_tifen=V_zong/V_fang;
k_dan=(k_xian-k_air*(1-V_tifen))/V_tifen
kk=0:0.01:1;
k_zheng=[];
for i=1:100
k_zheng=kk*V_tifen+k_air*(1-V_tifen);
end
figure
plot(k_zheng,kk,'r-')
title('单根与整体的热导率关系曲线图')
xlabel('单根热导率');
ylabel('整体热导率');
% 计算残差
residuals = k_zheng - kk * V_tifen - k_air * (1 - V_tifen);
% 绘制残差分布图(核密度估计图)
figure;
ksdensity(residuals);
title('残差分布图');
xlabel('残差');
ylabel('核密度估计');
clc;
clear;
% 提供的数据
time = [0; 0.02; 0.04; 0.06; 0.08; 0.10];
temperature = [25.000; 25.575; 25.693; 25.807; 25.896; 25.971];
% 进行指数拟合 (exponential model)
exp_fit = fit(time, temperature, 'exp2');
% 输出指数拟合的函数表达式
disp(['f(x) = ', formula(exp_fit)]);
% 生成插值点
interp_time = linspace(min(time), max(time), 100);
interp_temperature = feval(exp_fit, interp_time);
% 绘制原始数据和指数拟合曲线图像
figure;
plot(time, temperature, 'o', interp_time, interp_temperature, '-');
xlabel('时间');
ylabel('温度');
title('温度随时间变化图');
legend('原数据点', '指数拟合曲线');
grid on