差分方程模型：蛛网模型-编程知识

差分方程模型：蛛网模型

在完全竞争的市场经济中，一个时期某种消费品如猪肉的上市量远远大于需求量，由于销售不畅导致价格下降，生产者发现养猪赔钱，于是转而经营其它农副产品。过一段时间猪肉上市量就会下降，此时供不应求导致价格上涨，生产者看到有利可图，又转回来大规模养猪，这一样以来，下一个时期猪肉又会供大于求，价格下降，如果没有外界干预，这种市场现象将会循环往复。

【模型假设】

（1）某个时段商品的价格取决于商品的供给量；

（2）下一个时段商品的供给量取决于上一个时段商品的价格；

（3）常规商品，需求函数是减函数；供给函数是增函数。

【符号设置】

k ：时段，也是商品的生产和消费周期，k=1,2,…;

xk ：第k时段商品的数量，k=1,2,…;

yk ：第k时段商品的价格，k=1,2,…;

【建立模型】

在第k时段，根据假设（1），有

称为需求函数，供给商品越多，价格越低，yk为xk的减函数。

在第k+1时段，根据假设（2），有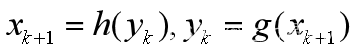【15】

这里h,g互为反函数，表示供给函数，为增函数。

即该种商品的供给与价格模型为

【16】

【模型分析】

1、平稳与非平稳现象分析

以供给量为横坐标，价格为纵坐标，在同一坐标系里绘制需求函数和供给函数，如图1和图2.

其中平衡点p0(x0,y0)由方程组求得

随着时段k的增加,xk,yk都不断震荡变化,p1,p2,…,pk并不收敛与p0.

即产品的市场价格和供给量将大起大落，不利于民生。

图1和图2的曲线分析市场稳定性的模型称为蛛网模型。其中f取决于消费者对该商品的需求程度和消费水平，g取决于生产者的生产能力、经营水平等。消费水水平增加时，曲线f向上移动；生产能力提高时，g向右移动。

2、平稳条件分析

通过调查资料一旦确定了需求函数和供给函数，商品数量和价格是否稳定，就完全由这两条曲线在平衡点p0附近的形状确定。

在平衡点p0附近，f和g都可以用直线来近似为【17】

在方程组【17】中消去yk，可得差分方程

【18】

【18】是一阶线性常系数差分方程，得到其特解为【19】

当k→+∞时，xk→x0（p0稳定）的充分必要条件是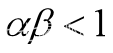【20】

3、模型参数解释

【17】

α表示商品供应每减少一个单位时价格上涨的幅度；β表示价格每上涨一个单位时，商品供应的增加量。α反应消费者对商品的需求敏感程度，β反应生产经营者对商品价格的敏感程度。当β固定时，α越小，需求曲线越平缓，市场越容易稳定；当α固定时，β越小，即供给曲线越陡，表明生产者对价格敏感程度越小，市场也容易趋于稳定。当α、β都较大时，表明消费者对商品过度敏感，生产者过度依赖价格，经济不稳定。

4、模型应用

当市场经济趋于不稳定时，政府有两种干预办法：

使得α尽量小，不妨考察极端情况，令α=0，即需求曲线水平，无论供应曲线如何，【20】条件总是成立，即市场总是平稳的。这种办法就是政府管控物价，无论商品数量多少，命令价格不得改变。
使得β尽量小，极端情况是β=0，即供应曲线竖直，于是无论需求曲线如何，也总是稳定的。实际上这相当于控制市场的商品数量，当供给量小于需求量时，从外地收购或调拨，投入市场；当供过于求时，收购剩余的部分，维持商场商品量不变。这种办法要求政府具有相当的经济实力。