1. 共现矩阵

将一句话的上下文大小窗口设置为1，用向量来表示单词频数，如：



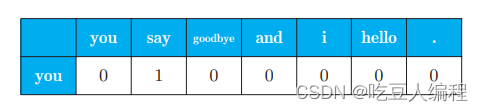
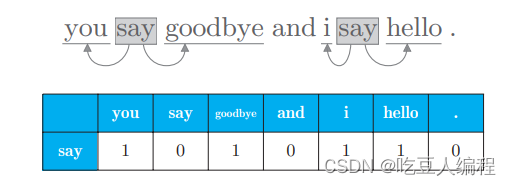
将每个单词的频数向量求出，得到如下表格，即共现矩阵：

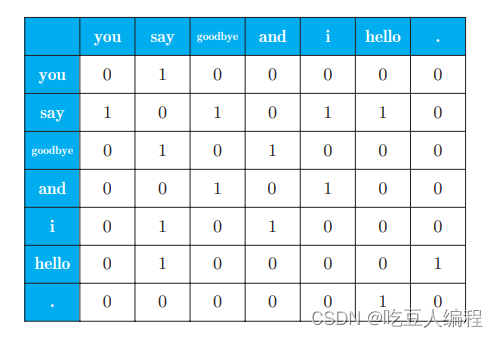
我们可以用余弦相似度（cosine similarity）来计算单词向量的相似性：
$\mathrm{similarity}(\mathbf{x},\mathbf{y})=\frac{\mathbf{x}\cdot \mathbf{y}}{\Vert \mathbf{x}\Vert \Vert \mathbf{y}\Vert }=\frac{x_1{y}_1+\cdots +x_n{y}_n}{\sqrt{x_1^2+\cdots +x_n^2}\sqrt{y_1^2+\cdots +y_n^2}}$

有时会出现分母为0的情况，在具体代码实现的时候，我们可以加上一个微小值，如1e-8

def cos_similarity(x, y, eps=1e-8):nx = x / (np.sqrt(np.sum(x ** 2)) + eps)ny = y / (np.sqrt(np.sum(y ** 2)) + eps)return np.dot(nx, ny)

2. 点互信息

在语料库中可能会看到很多“…the car…”这样的短语。实际上，与 the相比，drive和 car 的相关性更强。为了避免这种情况，可以引入PMI

$\mathrm{PMI}(x,y)={\log }_2\frac{P(x,y)}{P(x)P(y)}={\log }_2\frac{\frac{\mathbf{C}(x,y)}{N}}{\frac{\mathbf{C}(x)}{N}\frac{\mathbf{C}(y)}{N}}={\log }_2\frac{\mathbf{C}(x,y)\cdot N}{\mathbf{C}(x)\mathbf{C}(y)}$

P(x) 表示 x 发生的概率，P(y) 表示 y 发生的概率，P(x, y) 表示 x
和 y 同时发生的概率。PMI 的值越高，表明相关性越强。

这里假设语料库的单词数量（N）为 10 000，the 出现 100 次，car 出现 20 次，drive 出现 10 次，the 和 car 共现 10 次，car 和 drive 共现 5 次。

$PMI("the","car")=lo{g}_2\frac{10\cdot 10000}{1000\cdot 20}\approx 2.32$
$PMI("car","drive")=lo{g}_2\frac{5\cdot 10000}{20\cdot 10}\approx 7.79$

得出的PMI值，后者比前者要高，这是我们所需要的结果

3. 降维（奇异值分解）

奇异值分解（Singular Value Decomposition，SVD）。SVD 将任意矩阵分解为 3 个矩阵的乘积，如下式所示：

$X=US{V}^T$

上面的例子只考虑了一句话中少量单词的共现矩阵，如果我们使用一个真正的语料库，那么这个矩阵将变得十分庞大，这是一个很大的稀疏矩阵，我们需要对其进行降维，这里用到奇异值分解。
在numpy中可以用

U, S, V = np.linalg.svg()

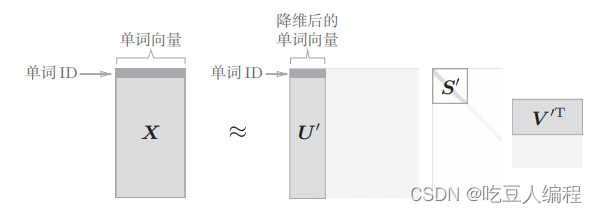
我们只需要取矩阵U的前两个元素即可将其降维到二维向量。