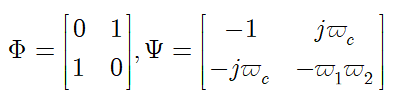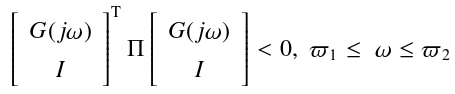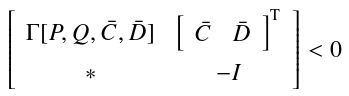目录
(一)Matlab中的LMI处理工具包
(二)为什么LMI成为控制理论领域重要工具?
(三)LMI在与Lyapunov不等式的关系
(1)线性矩阵不等式
(2)线性矩阵不等式系统
(3)舒尔(Schur)补
(四)LMI中常见引理
引理2(广义KYP引理[4])
推论1(广义KYP引理推论[4])
引理3(射影定理[1])
引理4 (Jensen不等式[5,6]
引理5 (Finsler's引理[7]):
参考文献
(一)Matlab中的LMI处理工具包
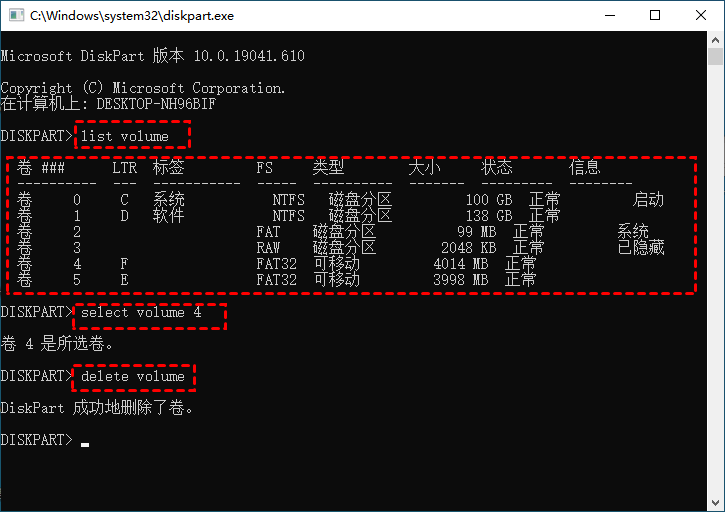
matlab中有专门求解线性矩阵不等式的工具包YALMIP,可以在官网上下载安装,可参考yalmip安装教程。yalmip只提供了一些基本的LMI求解方法,有更复杂的不等式求解需求可以再安装cplex工具包。关于怎么使用yalmip工具包可参考yalmip代码编写教程和LMI工具箱教程,教程文档。MONSK安装
(二)为什么LMI成为控制理论领域重要工具?
线性矩阵不等式(LMI)技术是分析和综合控制系统的重要工具,尤其是鲁棒控制领域,主要因素有以下三个[1]:
- 对于经典的控制方法,LMI技术的优点就是操作简单。在LMI技术出现以前,人们通过求解Ricaati方程来设计最优控制器,但是Ricaati方程求解很难。而LMI技术仅需少量的概念和基本原理就能开发出实用的工具(现在我们用YALMIP工具包就能很方便的求解LMI问题)。
- LMI技术提供了控制问题的广泛前景,包括鲁棒性分析,标称H∞,H2和鲁棒控制综合,多目标综合,线性参数变化综合,其中一些无法在古典控制领域中解决处理。
- LMI技术是利用凸优化的强有效的数值工具,并在理论体系上附加上有效的软件工具。
(三)LMI在与Lyapunov不等式的关系
(1)线性矩阵不等式
![]()
![]()
![]()
因此有:
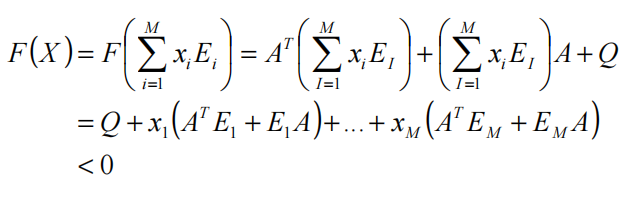
通过这种转化,就得到了一个更为一般的线性矩阵不等式的表达方式。
(2)线性矩阵不等式系统
假设存在多个矩阵不等式:
![]()
总体构成称线性矩阵不等式系统。引进,则
同时成立当且仅当
。因此一个线性矩阵不等式系统也可以用一个单一的线性矩阵不等式表示。
(3)舒尔(Schur)补
在许多一些非线性矩阵不等式转化成线性矩阵不等式的问题中,我们常常用到矩阵的Schur补性质。考虑一个矩阵![]() ,并将S分块:
,并将S分块:
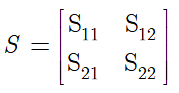
其中是
维的。假定
是非奇异的,则
![]() 称为“
称为“在S中的Sehar补”。以下引理给出了矩阵的Schur补性质。
引理1 Schur补性质
对给定的对称矩阵:
其中
是
维的。以下3个条件是等价的:
(1)
(2)
(3)
(证明方法可参考 俞立的《鲁棒控制——线性矩阵不等式处理方法》 p8页)
在一些控制问题中,经常遇到二次型矩阵不等式[3]:
![]()
其中是给定的适当维数的常数矩阵,
是对称矩阵变量,则应用引理1,可以将上面的矩阵不等式的可行性问题转化成一个等价的矩阵不等式:

的可行性问题,而后者是一个关于矩阵变量P的线性矩阵不等式。
因此在控制问题中,我们经常要设计Lyapunov函数V(t),并为了保证系统稳定性要求,那我们就可以把
这个不等式转化为线性矩阵不等式的形式,并用matlab中的YALMIP直接求解出即可。
(四)LMI中常见引理
引理2(广义KYP引理[4])
给定矩阵
,
以及
,
,且
代表
的零空间,其中
,则不等式
成立,当且仅当存在对称矩阵
以及
,使得
成立,其中
其中*表示矩阵的共轭转置,j是虚数单位,
表示右克罗内克积,即
推论1(广义KYP引理推论[4])
针对线性系统
,
为系统由扰动到控制输出的传递函数,则对于给定的对称矩阵
,下面两个陈述是等价的:
1)有限频域不等式
成立。
2)存在对称矩阵Р和Q满足Q>0,使得
成立,其中
且
表示矩阵
的右上块和右下块,矩阵中*表示其对应块的转置。
引理3(射影定理[1])
对于给定的标量
,矩阵
满足
,当且仅当下面两个条件成立:
引理3(反射影定理[1]):
是给定的正定对称矩阵,不等式
等价于下面的线性矩阵不等式(LMI)求解问题:
式中符号
用以表示矩阵
与其转置的加和,即
。
引理4 (Jensen不等式[5,6]
对于任意正定对称常数矩阵
,标量
满足
,并且存在一个向量
,那么以下不等式成立:
引理5 (Finsler's引理[7]):
令
,
,以及
满足H的秩小于n,rank(H) = r <n.则下列两式等价:
参考文献
【1】Apkarian P,Tuan H D,Bernussou J.Continuous-Time analysis,eigenstructure as-signment,and H2synthesis with enhanced Linear Matrix Inequalities(LMI)char-acterizations[J].IEEE Transactions on Automatic Control,2001,42(12):1941–1946.
【2】《鲁棒控制理论及应用》王娟 张涛 徐国凯
【3】《鲁棒控制——线性矩阵不等式处理方法》俞立
【4】Iwasaki T,Hara S.Generalized KYP Lemma:unified frequency domain inequal-ities with design applications[J].IEEE Transactions on Automatic Control,2005,50(1):41–59.
【5】Wu J,Chen X,Gao H.H∞filtering with stochastic sampling[J].Signal Proces-siong,2010,90(4):1131–1145.
【6】Gao H,Wu J,Shi P.Robust sampled-data H∞control with stochastic sampling[J].Automatica,2009,45(7):1729–1736.
【7】Qiu J,Feng G,Yang J.New results on robust energy-to-peakfiltering for discrete-time switched polytopic linear systems with time-varying delay[J].IET ControlTheory and Applications,2008,2(9):795–806.
·