目录
题目
例子
示例 1:
示例 2:
前言
思路
思想
代码
调用的函数
主函数
所有代码
力扣提交的代码
运行结果
小结
题目
给定一个三角形
triangle,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标
i,那么下一步可以移动到下一行的下标i或i + 1。
例子
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]] 输出:11 解释:如下面简图所示:23 46 5 7 4 1 8 3 自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]] 输出:-10
前言
本题是动态规划的一道经典题目,最早出现在1994年的ioi比赛中
经过了20多年的时间,如今已经变成了动态规划的入门必做题
思路
我们可以以下面的图来举例子
设置数据为一个二维数组(或者是一个容器)
放入[2],[3,4],[6,5,7],[4,1,8,3]四组数据

我们可以很简单的看出来——最短路径是2,3,5,1
如果把走到响应的点所得到的和(也就是所求值)定义为一个二维数组的话
我们可以得到一个4*4的二维数组(当然其中有一些是用不到了)
那可以把题目转化为求最底下行数组的值,并且比较大小得出最小值
我可以知晓除去第一列的值,其中随机一列的值只取决上一列与其相邻的值,因此我们可以设置递归函数,第a[i][j]的值只取决与原来数组本身的值加上a[i-1][j]与a[i-1][j-1]的最小值。
从底下迭代是一种方法
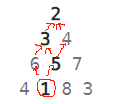
但是他会有一个问题,他会重复大量计算相同的数字
比如上面的例子:
第三行第一列以及第二列都需要知道第二行第一列的数字,所以第二行第一列的值会计算两遍
思想
所以结果就是我从上向下迭代
下一行的数字只会取上一行的值,然而上一行的值都是计算好的
不需要重新计算也不存在重复以及浪费时间

有些相当于广度优先了
那么思想有了
就是代码实现了
代码
调用的函数
int minimumTotal(vector<vector<int>>& triangle) {int length_1 = triangle.size();int length_2 = triangle[length_1-1].size();vector <vector<int>> n(length_1, vector<int>(length_1, 0));for (int i = 0; i <= length_1 - 1; i++){if (i == 0){n[0][0] = triangle[0][0];continue;}for (int j = 0; j <= i; j++){if (j == 0){n[i][0] = n[i - 1][0] + triangle[i][0];continue;}if (j == i){n[i][i] = n[i - 1][i - 1] + triangle[i][i];continue;}n[i][j] = min(n[i - 1][j - 1] + triangle[i][j], n[i - 1][j] + triangle[i][j]);}}int min = n[length_1 - 1][0];for (int i = 0; i <= length_2 - 1; i++)if (n[length_1 - 1][i] < min)min = n[length_1 - 1][i];return min;
}思想就是上面讲到的思想
需要注意的是第一行以及第一列与最后一列要单独考虑
主函数
int main()
{vector <vector<int>>sum_1 = { {2} ,{3,4},{6,5,7},{4,1,8,3} };int min = minimumTotal(sum_1);cout << min << endl;return 0;
}所有代码
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int minimumTotal(vector<vector<int>>& triangle) {int length_1 = triangle.size();int length_2 = triangle[length_1-1].size();vector <vector<int>> n(length_1, vector<int>(length_1, 0));for (int i = 0; i <= length_1 - 1; i++){if (i == 0){n[0][0] = triangle[0][0];continue;}for (int j = 0; j <= i; j++){if (j == 0){n[i][0] = n[i - 1][0] + triangle[i][0];continue;}if (j == i){n[i][i] = n[i - 1][i - 1] + triangle[i][i];continue;}n[i][j] = min(n[i - 1][j - 1] + triangle[i][j], n[i - 1][j] + triangle[i][j]);}}int min = n[length_1 - 1][0];for (int i = 0; i <= length_2 - 1; i++)if (n[length_1 - 1][i] < min)min = n[length_1 - 1][i];return min;
}
int main()
{vector <vector<int>>sum_1 = { {2} ,{3,4},{6,5,7},{4,1,8,3} };int min = minimumTotal(sum_1);cout << min << endl;return 0;
}力扣提交的代码
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {int length_1 = triangle.size();int length_2 = triangle[length_1-1].size();vector <vector<int>> n(length_1, vector<int>(length_1, 0));for (int i = 0; i <= length_1 - 1; i++){if (i == 0){n[0][0] = triangle[0][0];continue;}for (int j = 0; j <= i; j++){if (j == 0){n[i][0] = n[i - 1][0] + triangle[i][0];continue;}if (j == i){n[i][i] = n[i - 1][i - 1] + triangle[i][i];continue;}n[i][j] = min(n[i - 1][j - 1] + triangle[i][j], n[i - 1][j] + triangle[i][j]);}}int min = n[length_1 - 1][0];for (int i = 0; i <= length_2 - 1; i++)if (n[length_1 - 1][i] < min)min = n[length_1 - 1][i];return min;
}
};运行结果

小结
本期博客介绍了现在的动态规划的经典题目,并且提供了3种方法,
(入了个门,相当于?)