第一章说明

对于时间序列的研究，可以追溯到19世纪末和20世纪初。当时，许多学者开始对时间相关的经济和社会现象进行研究，尝试发现其规律和趋势。其中最早的时间序列研究可以追溯到法国经济学家易贝尔（Maurice Allais）和英国经济学家詹姆斯·克拉克（James Clark）的研究。随着时间序列分析方法的不断发展和应用，时间序列研究逐渐成为了统计学、经济学、金融学、工程学等领域重要的研究方向。

第二章、时态数据的结构

时间序列数据为

根据时间编制索引的观测值或测量值
而不是Xi，我们用Xt表示

为什么这会让事情变得不同？

时间索引具有特殊的排序。
随时间测量的数据不可交换，这是我们在索引数据时通常假设的我我.
时间也可以有其特殊的含义，代表其他未观察到的变量。

需要明确的是，时间序列数据的一个关键属性是，它与通常分析的其他类型的数据区分开来，我们不认为我们可以随机排列数据的索引并以相同的分布对数据进行建模。数据有排序。此外，数据独立的较强假设通常不适用。

时间序列数据的一个有趣且可能令人不安的特征是，原始形式的数据提供的真实信息很少。从某种意义上说，原始数据是最无用的数据形式。因此，绘制或汇总原始数据通常无法提供对正在发生的事情或为什么发生的很多见解。但是，由于时间索引具有如此特殊的意义，我们可以使用时间索引将时间序列数据分解为不同时间尺度的变化。时间尺度分析的正式方法有时称为傅里叶分析或光谱分析，但也有一些非正式方法也很有用。

考虑时间序列数据的另一种方法是，时间序列实际上表示在不同时间尺度上变化的时间序列的混合。分析时间序列数据的部分工作是

挑选时间尺度的混合并描述它们之间的区别
根据经验属性或手头的科学问题确定感兴趣的时间尺度

2.1 示例：空气污染与健康

例如，我们可能有兴趣研究长期暴露于环境空气污染如何影响您的预期寿命。例如，一些研究表明，与生活在更清洁的城市相比，一生生活在污染更严重的城市会使您的预期寿命减少多达 6 个月。在考虑如何解决这个问题以及如何分析数据时，我们主要感兴趣的是比较城市之间的长期平均污染水平，也许是几十年。我们不太可能关心某一天甚至一个月的污染水平有多高。

另一方面，许多研究表明，空气污染的短期峰值会增加一个城市的心血管和呼吸系统疾病的死亡人数和住院人数。在这种情况下，我们可能有兴趣将空气污染的日常变化与住院或死亡率的日常变化进行比较。总体长期平均污染水平没有什么意义。

考虑以下 10–1987 年期间密歇根州底特律的颗粒物（PM1999）数据的时间序列图。

有人可能会问一个看似简单的问题：底特律的空气污染在1987年至1999年期间有所改善吗？事实上，在这段时间内，污染水平总体上略有下降，但持续不断。

实际上，当我们查看拟合的简单线性回归模型结果时，我们看到斜率的系数为负。

# A tibble: 2 x 5term        estimate std.error statistic   p.value<chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept) 48.4      1.67         28.9  9.59e-170
2 date        -0.00157  0.000184     -8.54 1.77e- 17

但是，在查看上面的图时，很难不注意到定期发生的极端峰值。粗略阅读该图显示了PM10水平达到100 \（mu\）g/m\（^3\）的天数。因此，底特律的PM10随着时间的推移而下降，但我们在某些日子里仍然会经历高水平。情况是否有所改善？

当然，答案与我们考虑数据的时间尺度有关。在长期的时间尺度上，事情似乎正在减少，因此趋势平稳。然而，在短期时间尺度上，我们仍然会看到大的峰值。没有一个答案;答案取决于时间尺度。

从政策角度来看，我们可以采用不同的策略来影响长期和短期时间尺度的空气污染。为了长期改变污染水平，我们可能会尝试将当地经济从基于化石燃料的能源转变为更可再生、污染更少的能源。这样的计划可能会产生重大影响，但需要大量时间才能实施。为了应对污染的短期波动，我们可能会实施交通禁令或有针对性的基于源的干预措施等政策，以缓解短期高峰。

现在假设我们想看看底特律的死亡率和空气污染之间是否存在任何关联。我们可以制作一个简单的散点图来查看是否存在简单的关联。

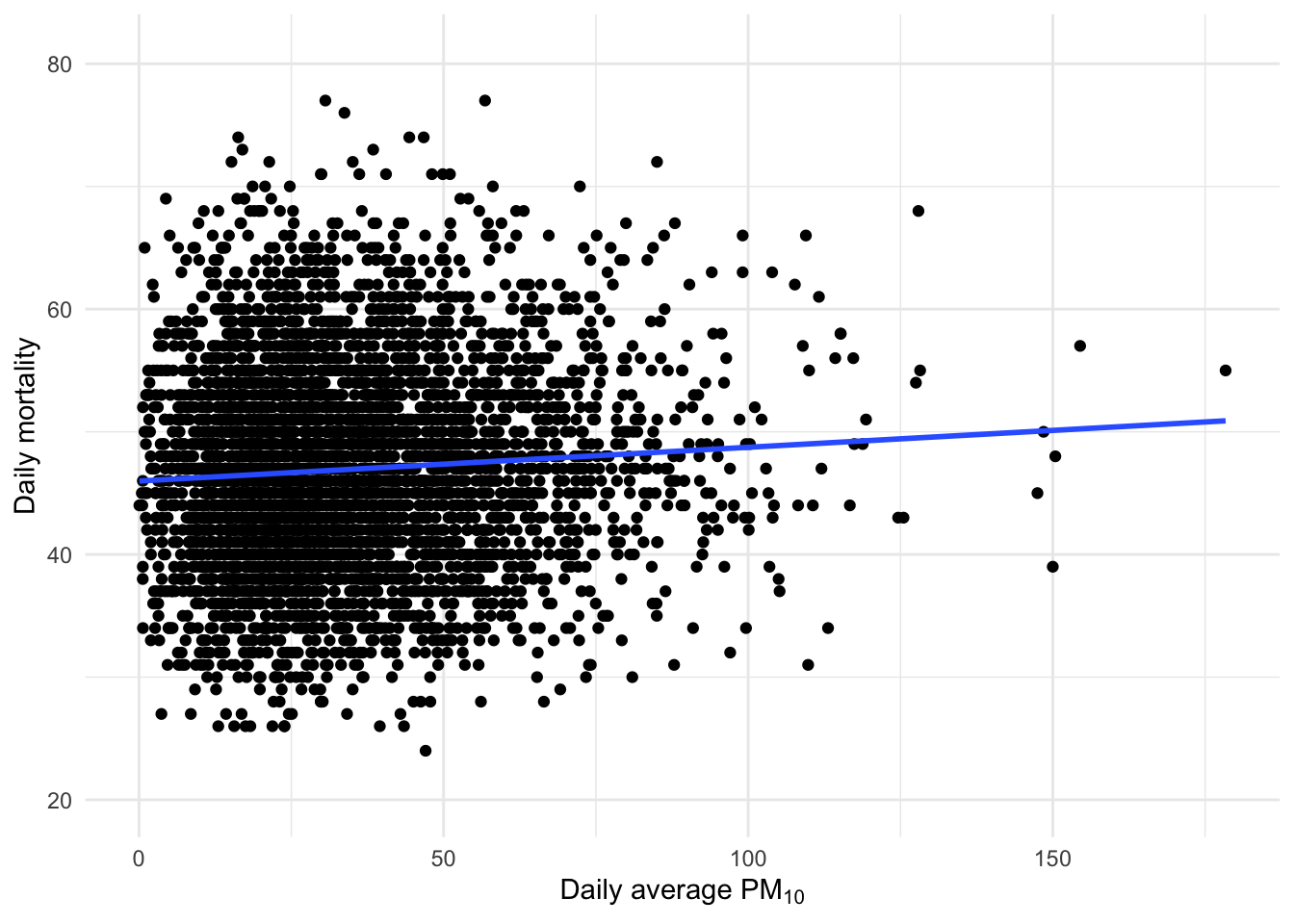
现在，这个散点图是我们在没有时间序列数据时可能会制作的。但是，由于我们确实有时间序列数据，因此我们应该立即开始根据不同的时间尺度变化来思考问题。我们关心的是污染和死亡率之间的长期关联，还是关心短期关联？

上图中显示的整体关联可以用简单的线性回归模型进行量化。

# A tibble: 2 x 5term        estimate std.error statistic    p.value<chr>          <dbl>     <dbl>     <dbl>      <dbl>
1 (Intercept)  46.0      0.226      204.   0         
2 pm10          0.0275   0.00564      4.88 0.00000108

两者之间似乎存在正相关，表明空气污染水平的增加与死亡率的增加有关。但是，我们能做更多的事情来获得更多的洞察力吗？

让我们计算PM10的年平均值，并对年度死亡总数求和，并制作这些年度汇总统计数据的散点图。

从这个图中我们可以看到，这种关联似乎相当强（当然，只有 13 个数据点）。当我们为这些数据拟合线性模型时，我们得到以下内容。

# A tibble: 2 x 5term        estimate std.error statistic       p.value<chr>          <dbl>     <dbl>     <dbl>         <dbl>
1 (Intercept)   10388.     987.      10.5  0.00000000725
2 pm10            190.      29.4      6.47 0.00000579

从一年到下一年，年平均PM10变化一个单位，与190.4例死亡的变化有关。

现在，我们可以将PM10的每日偏差与其年平均值进行比较，并查看该偏差与每日死亡率之间的关联。

# A tibble: 2 x 5term        estimate std.error statistic p.value<chr>          <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)  46.9      0.116      404.    0     
2 pm10dev       0.0142   0.00574      2.47  0.0136

这里的关联要小得多，但当然我们只关注PM10的每日变化，而不是年度变化。我们预计PM10从一天到第二天的一个单位变化会带来大量死亡。

人们可能会想知道：哪个估计是正确的？是日平均PM10与死亡率之间的关联，还是年平均PM10与死亡率之间的关联？答案是两者都是“正确的”，但每个都回答了不同的问题。日平均值着眼于短期变化，可以解释为代表污染的“急性”影响，而年平均值可能会重新反映空气污染水平的“慢性”影响。

在不同时间尺度上观察关联时要考虑的另一个问题是，在这个时间尺度上存在的混杂因素是什么？在观察PM10的逐年变化时，可能存在许多混杂因素，这些混杂因素也因PM10和死亡率而异。在观察PM10的每日变化时，每年平稳变化的相同混杂因素可能不会引起关注。但是，可能还有其他混杂因素每天都需要考虑。

2.2 固定变化与随机变化

大多数时间序列书籍倾向于将时间序列想象为仅由随机现象组成，而不是固定和随机现象的混合。因此，建模通常侧重于时序模型的随机方面。然而，世界上许多实时序列是由我们可能认为的固定和随机变化组成的。

温度数据具有非“随机”的昼夜和季节性成分
空气污染数据可能会根据交通或通勤模式产生星期的影响

虽然有时很容易将一切都视为随机的，但当我们缺乏对真正潜在现象的观察时，这通常是一根拐杖。此外，当某些东西是固定的时，将它视为随机将导致违反我们通常做出的平稳性假设（见下文）。

根据应用程序的性质，对固定或随机的相同现象进行建模可能是有意义的。换句话说，这取决于。

在生物医学和公共卫生应用中，我们通常处理完全观察到的数据集，并试图解释“发生了什么？
我们正在描述过去，也许是对未来做出推断
在金融或控制系统应用中，我们可能会根据过去对未来事件进行预测。从过去数据中看似固定的事情将来可能会发生变化，因此我们可能希望允许模型“适应”未知的未来模式。

考虑以下 1990–1992 年马里兰州巴尔的摩的日平均温度图。正如人们从温度数据中预期的那样，有一个强烈的季节性模式，在夏季达到顶峰，在冬季出现低谷。

现在，这种所谓的季节性模式是固定的还是随机的？历史告诉我们，季节性模式是相当可预测的。我们通常不相信夏天可以冻僵，冬天也可以达到90度（F）。

讨论此问题的更正式方式可能是使用以下模型。设 \（y_1， y_2， \dots\）是巴尔的摩每天 \（t\）的温度值，并考虑以下模型，

\[ y_t = \mu + \varepsilon_t， \]

其中 \（\varepsilon\）是期望值 \（\mu\）和观测值 \（y_t\）之间的随机偏差。在没有任何计算机的帮助下，我们可能会查看上面的图并估计\（\mu\）大约是50-55度。但是现在，假设您的工作是预测 \（t\）的任何值的 \（\varepsilon_t\）的值。很明显，如果 \（t\）在年中下降，则很可能是 \（\varepsilon_t > 0\），如果 \（t\）在年初或年底附近下降，那么很可能是 \（\varepsilon_t < 0\）。因此，我们只需知道 \（t\）的值即可获得有关偏差 \（\varepsilon\）的重要信息。换句话说，序列\（\varepsilon_t\）中嵌入了一个固定的季节性效应，我们可能很难将其视为“随机”。

但现在考虑以下模型。

\[ y_t = y_{t-1} + \varepsilon_t。 \]

此模型将 \（y_t\）的值预测为与时间 \（t-1\）处的值的偏差。所以今天的值等于昨天的值加上一个小的偏差。现在，假设您的工作是预测 \（\varepsilon_t\）的值。这有点难，对吧？如果我知道昨天是70度，我确定今天会比70度温暖吗？还是更冷？如果我知道昨天是20度，我确定今天会更暖和还是更冷？在此模型中，偏差\（\varepsilon_t\）可能看起来更“随机”或更难预测。没有一个固定的规则说今天的温度总是比昨天的温度更暖（或更冷）。

考虑下面的不同时间序列，它显示了股票代码为 SPY 的交易所交易基金的加权中间交易价格。该基金追踪美国股票的标准普尔500指数。请注意，x 轴上的时间刻度以微秒为单位。

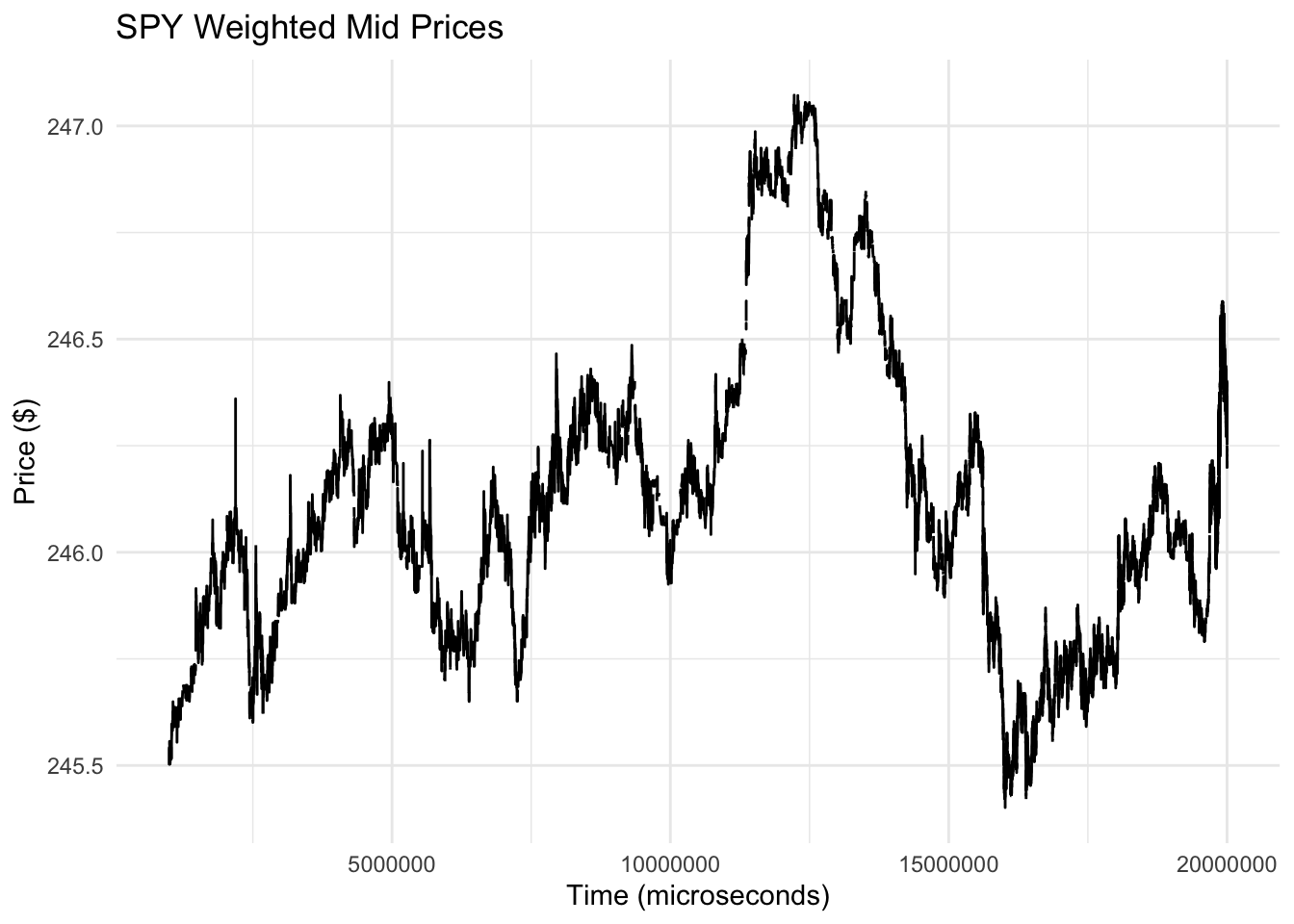
与温度时间序列相比，该图看起来不那么规则，并且没有可识别的模式。此外，在微秒级，我们可能不太熟悉这种股票价格可能存在的固定模式。有经验的交易者可能知道，在一天中的给定时间，在几十万微秒的窗口内，这种模式总是会出现。

然而，对于金融，有一种被称为有效市场假说的理论认为这种固定模式不应该存在。如果存在这样一个固定的模式，它将代表一个套利机会，或者一个没有风险的赚钱机会。例如，在上面的图中，我们可以在 2 万微秒的时间买入股票，然后在 5 万微秒左右卖出，以获得轻松的利润。如果这种模式每天都存在，我们可以告诉我们的经纪人每天执行这笔交易以获得微薄的利润。然而，随着这种模式的消息泄露到市场上，越来越多的人会开始和我同时买入，和我同时卖出。这将在买入时提高价格，在卖出时降低价格，最终获利机会将消失。

有效市场假说表明，这种固定模式的存在极不可能。因此，将此类数据建模为随机数据可能更有意义，而不是固定数据。这表明可以采用不同的建模策略和不同类型的模型。我们不会在这里详细讨论这些类型的模型。