【机器学习】训练集/验证集/测试集释疑-编程知识

文章目录

- - 序言
  - 1. 训练集、验证集、测试集是什么
  - 2. 为什么需要验证集
  - 3. 验证集是必须的吗
  - 4. 验证集和测试集上的表现会不同吗
  - 5. 如何从Train/Test Set划分Validation Set
  - 6. 训练集、验证集和测试集的比例怎么设置
  - 7. 模型表现不好时测试集可以反复使用来调整模型吗
  - 8. 训练集、验证集和测试集的数据是否可以有所重合
  - 9. 常见的机器学习模型验证方法有哪些

序言

关于数据集的一些疑问厘清

1. 训练集、验证集、测试集是什么

训练集：Training Dataset. 用于训练和调整模型参数
- 训练阶段
验证集：Validation Dataset. 用于验证模型精度和调整模型超参数
- 模型挑选阶段
- 验证集的作用体现在训练的过程中
- 比如：通过查看训练集和验证集的损失值随着epoch的变化关系可以看出模型是否过拟合，如果是可以及时停止训练，然后根据情况调整模型结构和超参数，大大节省时间
测试集：Test Dataset. 验证模型的泛化能力
- 验证阶段
- 测试集的作用体现在测试的过程中

2. 为什么需要验证集

首先，划分训练集、验证集和测试集，能够避免信息泄漏
模型的参数和超参，模型存在两个最优：训练集参数的最优 + 超参数的最优。如果没有验证集，假设训练好的模型在测试集上表现不好，将无法确认是模型参数过拟合/欠拟合，还是超参数设置不合理，所以需要验证集来选择超参数
验证集和测试集一样，都是未知的，如果模型适用于验证集，那么也大概会适用于测试集

3. 验证集是必须的吗

否
训练集是练习题 + 验证集是模拟题 + 测试集是考试题
训练集：调试网络参数；验证集：没有参与网络参数更新
没有超参数就不需要验证集。如果不需要调整超参和early stop，就不需要验证集，把验证集并入训练集即可，但是不需要超参的模型比较少见
验证集是用来选取最优超参数的
在实际应用中，有可能不继续划分验证集和测试集，就相当于假设验证集和测试集分布高度相似，依次来验证开发算法的泛化性能

4. 验证集和测试集上的表现会不同吗

会不会出现调优后的超参数在验证集上优秀，但在测试集上却表现不如模型超参数？
一般不会，除非验证集和测试集的数据分布有明显不同

5. 如何从Train/Test Set划分Validation Set

从training set中拿出一部分作为validation set，最好让validation set和test set的大小和数据分布接近。如下

6. 训练集、验证集和测试集的比例怎么设置

如果有惯例，按照惯例
没有的话，可以是10:1，8:2，7:3，6:4等。传统上是6:2:2，即训练集:验证集:测试集 = 6:2:2是可以的
如果不需要验证集，训练集：测试集 = 8:2或7:3
网上还看到两种划分比例：
- 训练集：验证集：测试集 = 8：0.5：1.5
- 训练集：验证集：测试集 = 7：1：2
数据集划分没有明确规定，但可以参考以下原则
- 对于小规模样本集（几万量级），常用的分配比例是 60% 训练集、20% 验证集、20% 测试集
- 对于大规模样本集（百万级以上），只要验证集和测试集的数量足够即可。例如有 100w 条数据，那么留 1w 验证集，1w 测试集即可。1000w 的数据，同样留 1w 验证集和 1w 测试集
- 超参数越少，或者超参数很容易调整，那么可以减少验证集的比例，更多的分配给训练集

7. 模型表现不好时测试集可以反复使用来调整模型吗

如果只是调整超参数，那么重复使用测试集属于作弊
如果不光调整超参、还对模型设计、训练方法做改进，可以重复使用

8. 训练集、验证集和测试集的数据是否可以有所重合

数据少，又不想使用数据增强，可以使用交叉验证的方法
但各数据集的数据肯定都是划分清楚的

9. 常见的机器学习模型验证方法有哪些

（1）留出法
- 按照固定比例将数据集固定的划分为训练集、验证集、测试集
（2）k折交叉验证
- 留出法对数据的静态划分可能得到不同的模型；k折交叉验证是一种动态验证的方法，可以降低数据划分带来的影响
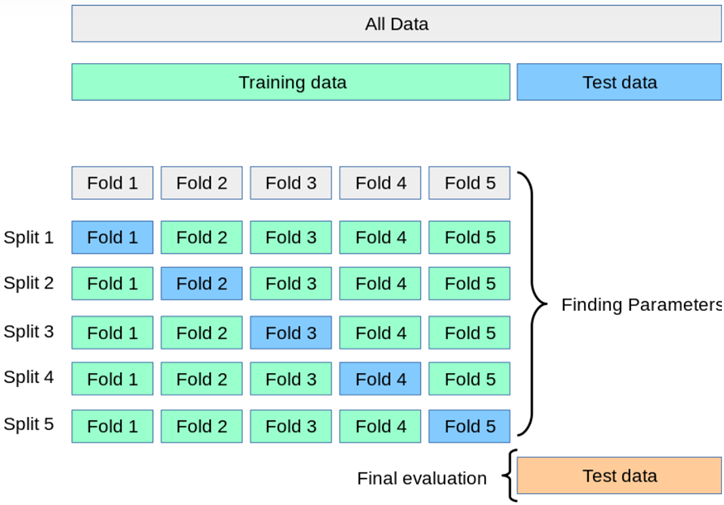
- 步骤：
  - 1）将数据集分为训练集和测试集，将测试集放在一边
  - 2）将训练集分为 k 份
  - 3）每次使用 k 份中的 1 份作为验证集，其他全部作为训练集
  - 4）通过 k 次训练后，我们得到了 k 个不同的模型
  - 5）评估 k 个模型的效果，从中挑选效果最好的超参数
  - 6）使用最优的超参数，然后将 k 份数据全部作为训练集重新训练模型，得到最终模型
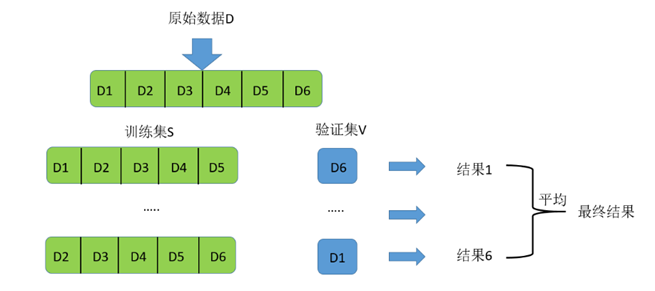
  - 7）还有一种说法是，将k次loss的平均作为性能度量得到最终模型，如下图
（3）留一法
- 是k折交叉法的一个变种，将k定义为n（n为样本数）
- 一般在数据缺乏时使用，即适合于小样本的情况，优点是样本利用率高，缺点是计算繁琐
- 每次的测试集都只有一个样本，要进行 n 次训练和预测
- 这个方法用于训练的数据只比整体数据集少了一个样本，因此最接近原始样本的分布。但是训练复杂度增加了，因为模型的数量与原始数据样本数量相同
（4）自助法
- 自助法以有放回/自助采样为基础
- 每次随机从 $D$ （样本数为m）中挑选一个样本，放入 $D^{'}$ 中，然后将样本放回D中，重复m次之后，得到了包含m个样本的数据集 $D^{'}$
- 样本在m次采样中始终不被采到的概率是
  $(1-\frac{1}{m} )^{m}$
- 取极限得到
  $\lim_{m \to \infty} (1-\frac{1}{m} )^{m} =\frac{1}{e} =0.368$
- 即D约有 $36.8\%$ 的样本未出现在 $D'$ 中。于是将 $D'$ 用作训练集， $D$ \ $D'$ 剩下的用作测试集
- 这样，仍然使用m个训练样本，但约有1/3未出现在训练集中的样本被用作测试集
- 这种方法优点是自助法在数据集较小、难以有效划分训练/测试集时很有用；自助法改变了初始数据集的分布，这会引入估计偏差