波奇学C++：AVL树-编程知识

AVL解决二叉搜索树退化成链表，保证左右子树高度不差过1，尽可能接近满二叉树

AVL树的性质：高度差（平衡因子）的绝对值不超过1（-1/0/1）

平衡因子：右子树高度-左子树高度

用平衡因子控制高度

AVL树节点

class AVLTreeNode
{pair<K, V>_kv; //key/valueAVLTreeNode<K, V>* _left; // 左AVLTreeNode<K, V>* _right;// 右AVLTreeNode<K, V>* _partent;// 父母int _bf;// 平衡因子AVLTreeNode(const pair<K,V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};

控制逻辑：增加一个新节点cur

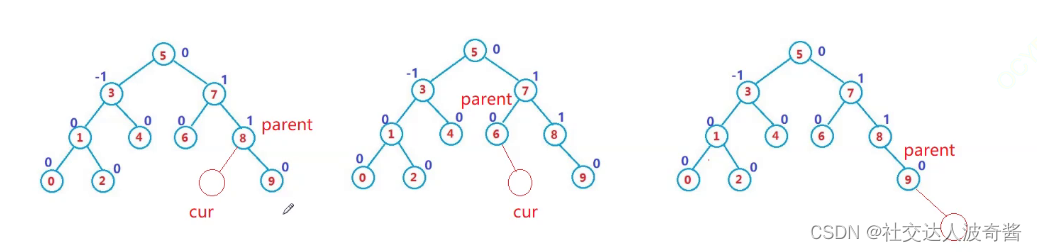
parent的bf值-1，在右，parent的bf加1

如果parent_bf=0，则不再改变，否则继续向上调整，直到parent为0，或者为cur为根节点时。

如果parent的平衡因子为2或者-2，说明树不平衡，要进行旋转调整。

当左边高时(parent=2，cur=1)

柱子a,b,c表示高度为h的AVL树

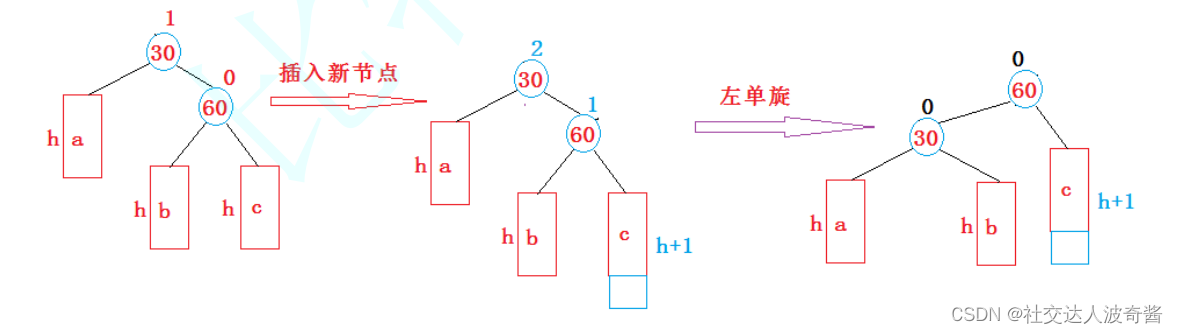
parent->right=cur->left
cur->left=parent

对于左单旋的理解:1.根节点向左转，2.c树高度增加后a树高2，于是把c的父节点当成根节点使得c的高度方向-1，a的树的方向+1，刚好平衡

同时调整平衡因子数量和parent指针

左单旋

void RotateL(Node* parent){Node* cur = parent->_right; //确定curNode* curleft = parent->_left;parent->_left = curleft;//当h不为0时if (curleft){//调整parent指针curleft->_partent = parent;}cur->_left = parent;//调整新的根节点的parent指针Node* ppnode = parent->_parent;parent->_parent = cur;//根节点特殊情况if (parent == _root){_root = cur;cur->_partent = nullptr;}else{// 确定parent是ppnode的左指针还是右指针if (ppnode->_left==parent){ppnode->_left = cur;}else{ppnode_right = cur;}cur->_partent = ppnode;}parent->_bf = cur->_bf = 0;}

void RotateR()
{void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;cur->_right = parent;Node* ppnode = parent->_parent;if (curright){curright->_partent = parent;}parent->_parent = cur;if (ppnode == root){_root = cur;cur->_partent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else(ppnode->_right == parent){ppnode->_right = cur;}}cur->_bf = parent->_bf = 0;}
}

双旋：我们发现左右双旋都是在都是a,c树高度发生变化，具体体现在cur和parent的平衡因子都是相差1，而如果在b树发生变化，无论是左边高还是右边高都会产生双旋问题。具体可以分为四种情况,现在以一种情况为例：

如下图是右边高的b树（现为60-b-c子树）发生改变。

从图上来讲是90进行右旋，把高的树的树移到外面，再30进行左旋，构建平衡。

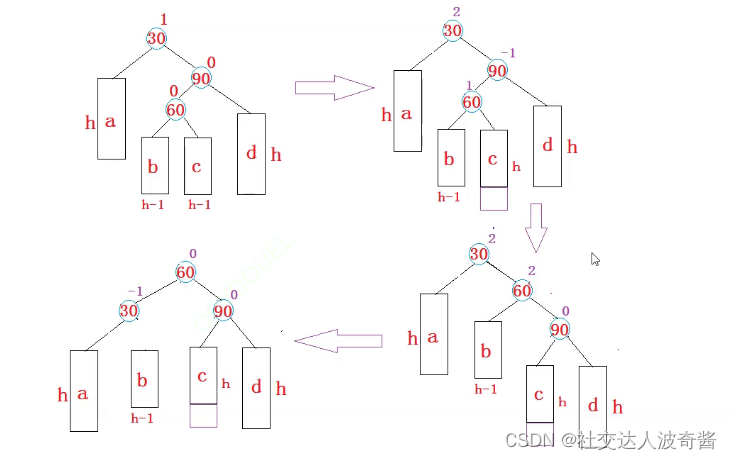
对于父节点为60的树来说，左树成为30节点的右树，右树成为90节点的左树。

所以60的节点的双旋后30，60，90的_bf值不恒为0，30,90节点会受到60的影响。

当60->_bf=1, 30,60,90 =-1 ,0,0

60->_bf=-1, 30,60,90 = 1,0,0

当

左高右高的区别都是60做根节点，且_bf变化是一样的。

左高：先左旋后右旋，右高，先右旋后左旋。

插入代码和旋转代码

bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else if (parent->_kv.first > kv.first){parent->_left = cur;}cur->_parent = parent;return true;// 更新节点while (parent){if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){//右高双旋RotateRL(parent);}else{//左高双旋RotateLR(parent);}}else{assert(false);}}return true; }void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = parent->_left;parent->_left = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left==parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}	void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;cur->_right = parent;Node* ppnode = parent->_parent;if (curright){curright->_parent = parent;}parent->_parent = cur;if (ppnode == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}}cur->_bf = parent->_bf = 0;}//右高先右后左void RotateRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 1){cur->_right->_bf = 0;cur->_left->_bf= -1;}else if (bf == -1){cur->_right->_bf = 0;cur->_left->_bf = 1;}else{;}}void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(cur);RotateR(parent);if(bf == 1){cur->_right->_bf = 0;cur->_left->_bf = -1;}else if(bf==-1){cur->_right->_bf = 0;cur->_left->_bf = 1;}else{;}}

检验AVL树

int Height(Node* root){if (root == nullptr)return true;int leftHight = Height(root->_left);int right = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeigth + 1;}bool IsBalance(Node* root){if (root == nullptr)return true;int leftHight = Height(root->_left);int rightHight = Height(root->_right);if (rightHight-leftHight!=root->_bf){cout<<"平衡因子异常"}return abs(rightHight - leftHight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right);}