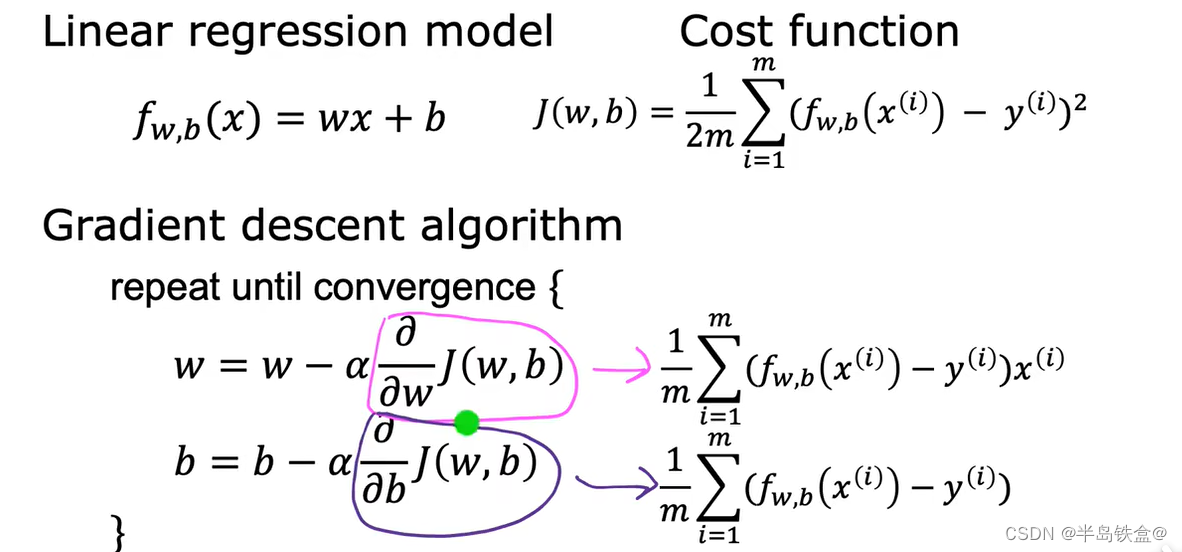
1.线性回归模型
2. 损失函数
3.梯度下降算法
多元特征的线性回归
当有多个影响因素的时候,公式可以改写为:
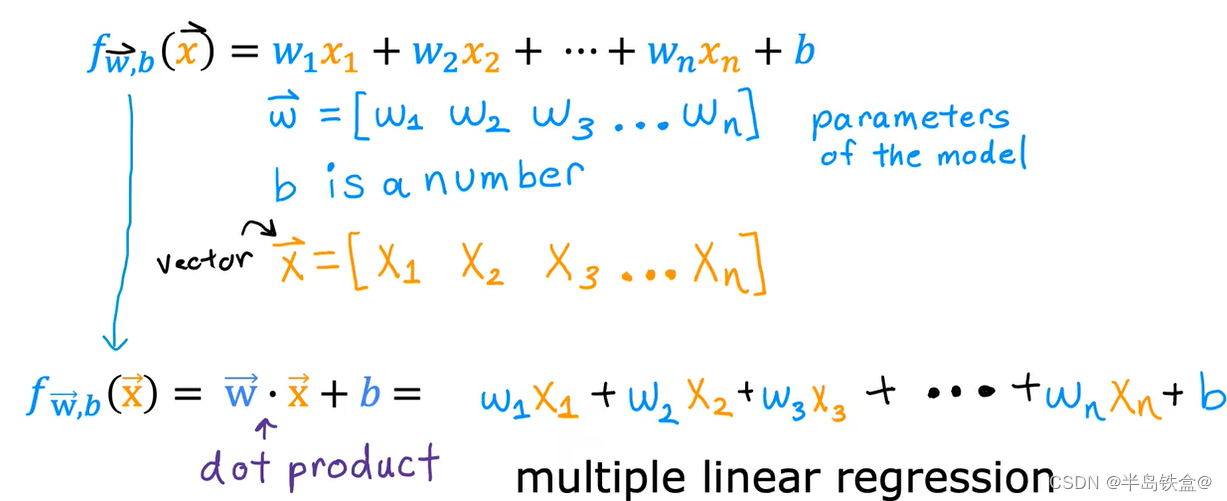

当有多个影响因素的时候为了方便计算,可以使用 Numpy下面的点积方法, np.dot(w,x) 最后再加个b
就省略了很多书写步骤,这叫做矢量化
多元回归的梯度下降
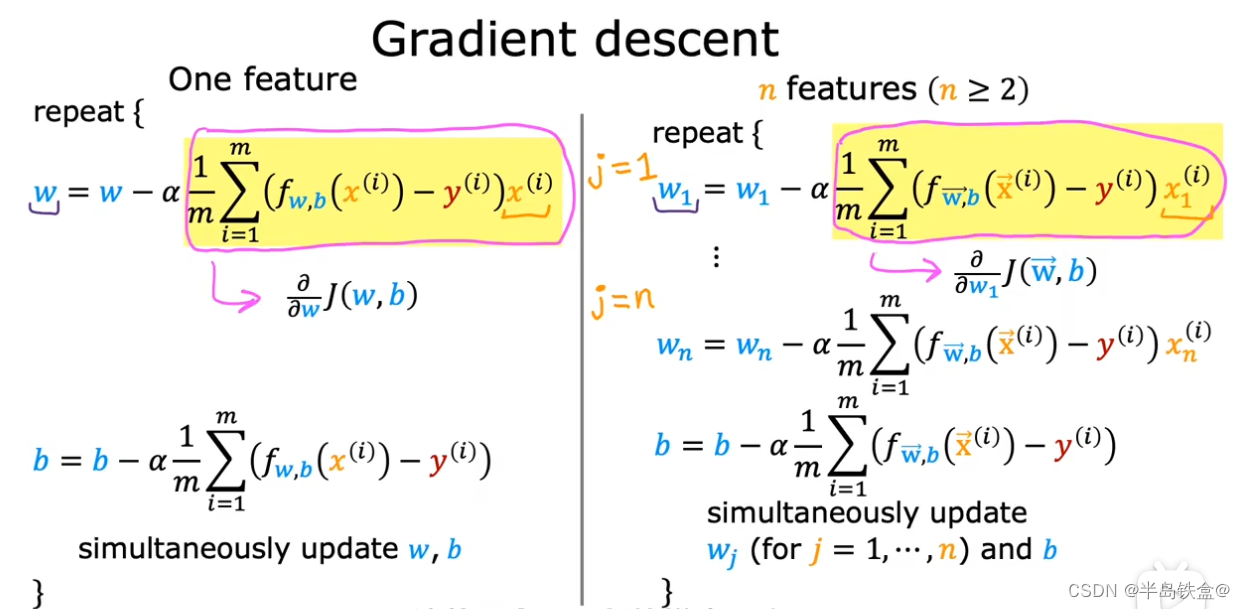
左边是一元的,只需要更新一个w,
右边是多元的,需要对多个w进行梯度下降
特征缩放
假设特征1的范围为 5~2000
特征2的范围为0~5
有三种方法可以实现特征缩放
1.除以最大值法:
5~2000 除以2000 变成 0.0025~1
0~5 除以 5 变成 0~1
2.归一化
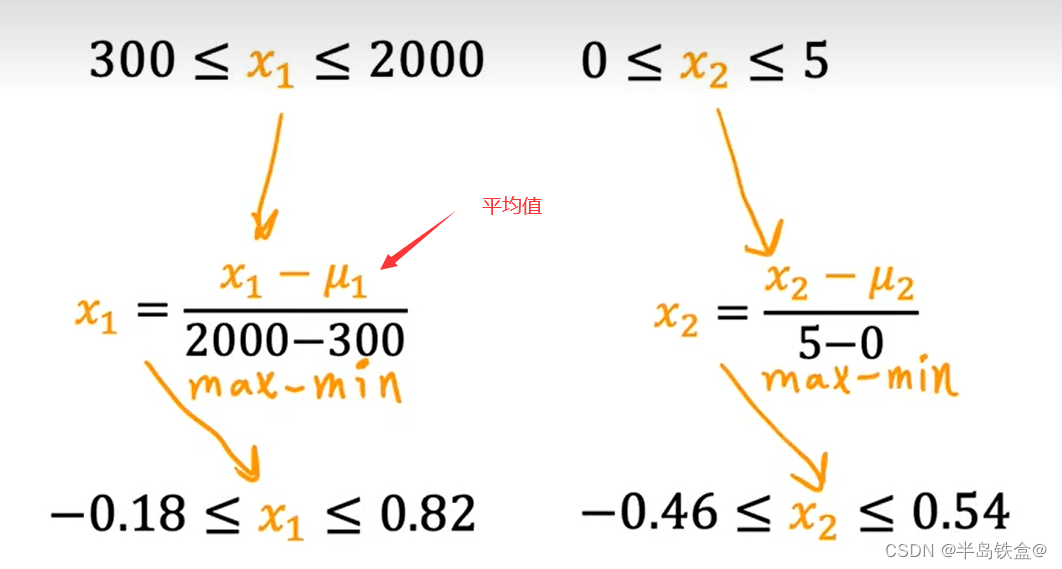
3.z-score
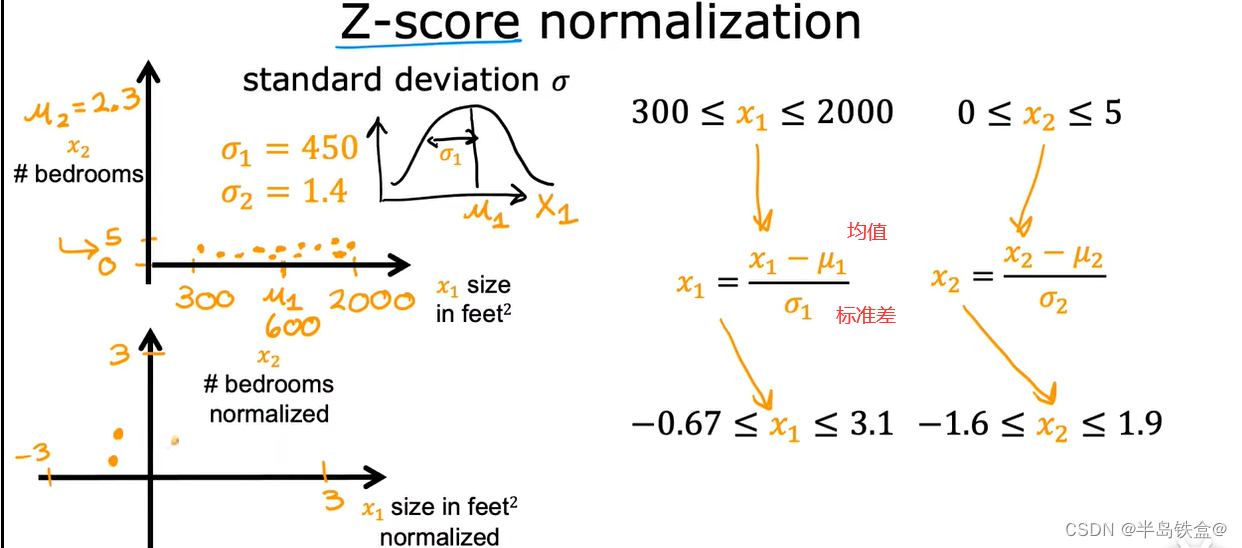
数据太大,或太小,需要进行特征缩放,来加快梯度下降的效率
逻辑回归
该模型常用于分类问题, 比如分辨 良性肿瘤和 恶性肿瘤
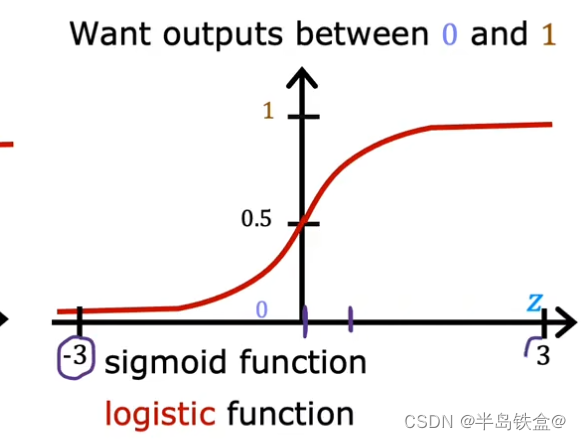
上图为 sigmoid函数
数学公式如下
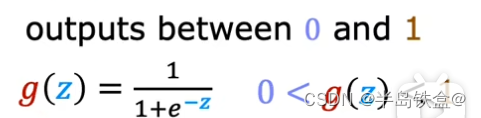
公式推导如下
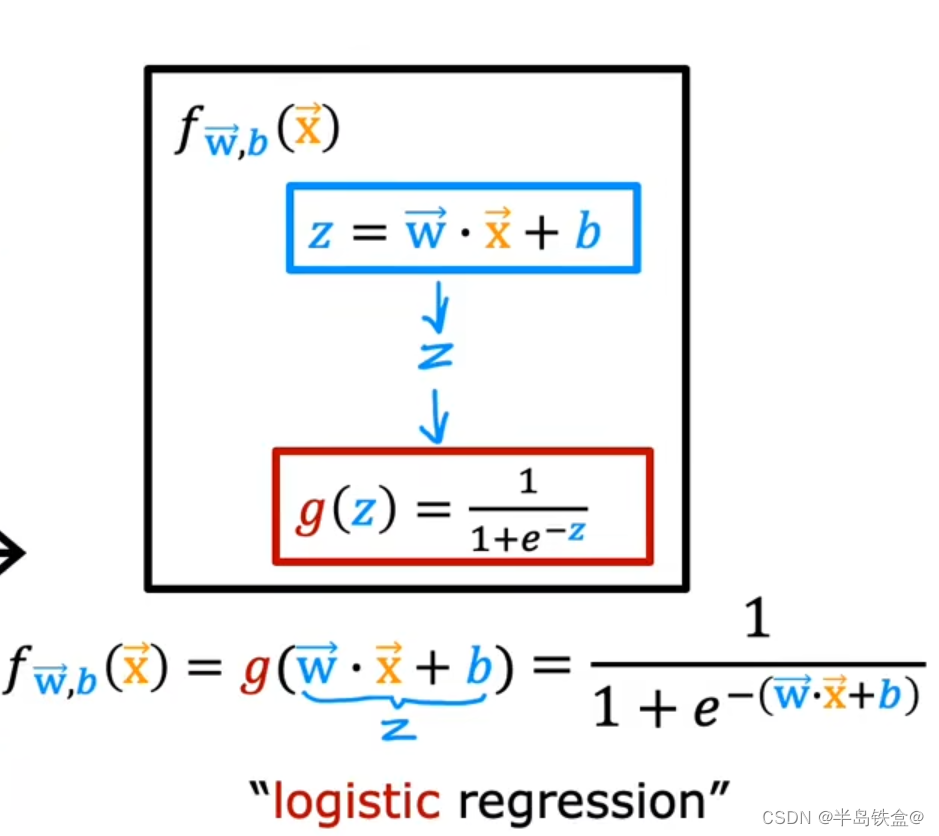
既然分类那么需要决策边界
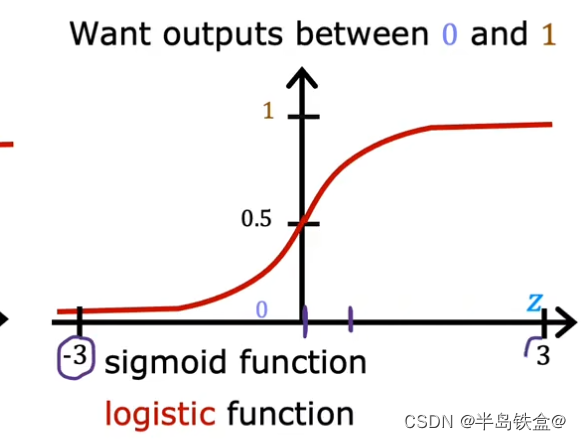
当Z>0时 即 y>0.5 时 类型为 1 ;Z = wx + b 即 wx + b > 0
当Z<0时 即 y<0.5 时 类型为 0; wx + b < 0
逻辑回归的损失函数
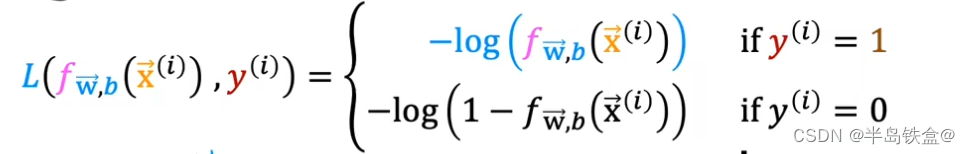
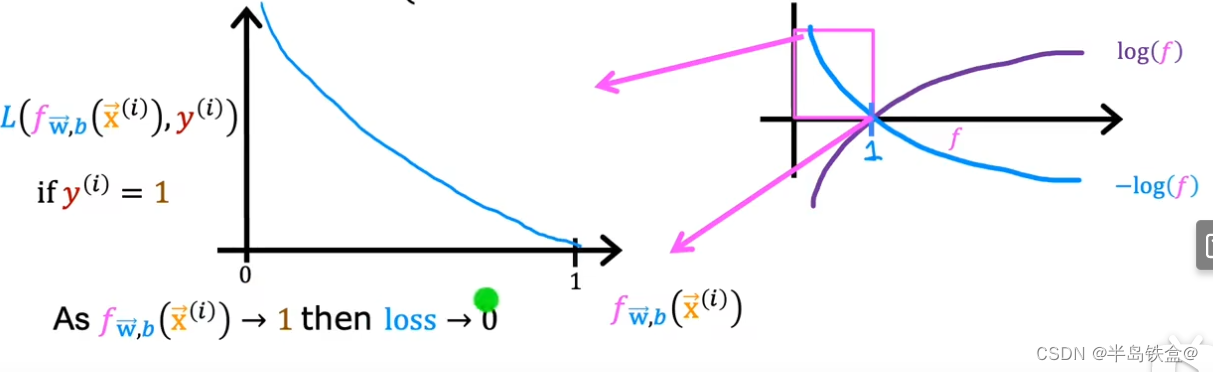
如图所示,当y=1时,损失很低符合要求
如图所示当y = 0 时 损失函数如下,发生了图像变换, 先关于y轴对称,然后向右平移一个单位
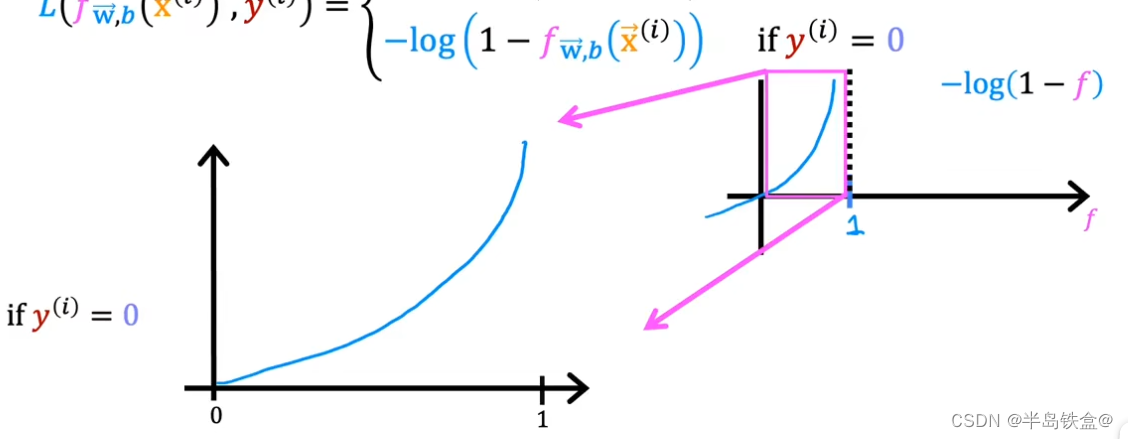
等价于

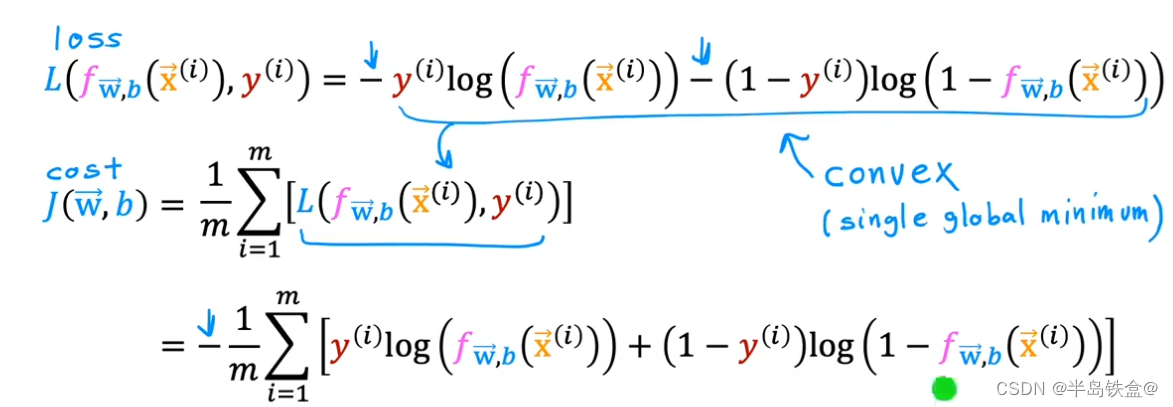
J, 这里的y只能去0或1 ,因为这是一个分类问
逻辑回归的梯度下降
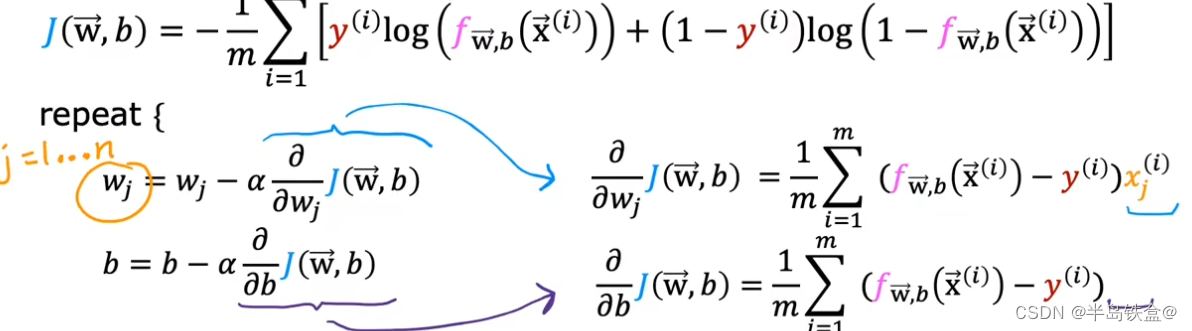
发现跟线性回归的梯度下降一样
但是两者的区别是f(x)不同
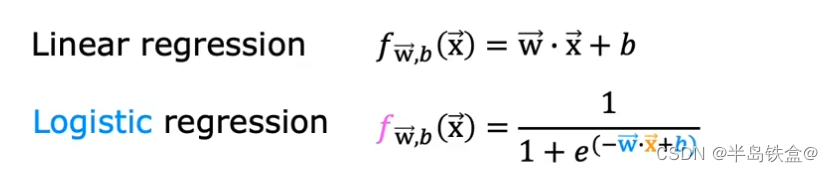



![2023年中国智能电视柜产量、需求量、市场规模及行业价格走势[图]](https://img-blog.csdnimg.cn/img_convert/f189ab4f3166845d1771bce82cd76bdf.png)


