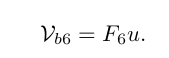01背包
题目
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
代码
function testWeightBagProblem (weight, value, size) {// 定义 dp 数组const len = weight.length,dp = Array(len).fill().map(() => Array(size + 1).fill(0));// 初始化for(let j = weight[0]; j <= size; j++) {dp[0][j] = value[0];}// weight 数组的长度len 就是物品个数for(let i = 1; i < len; i++) { // 遍历物品for(let j = 0; j <= size; j++) { // 遍历背包容量if(j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}console.table(dp)return dp[len - 1][size];
}function test () {console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
}test();
01背包理论基础(滚动数组)
思路
-
确定dp数组的定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。 -
一维dp数组的递推公式
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
-
一维dp数组如何初始化
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
那么我假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。 -
一维dp数组遍历顺序


-
代码
function testWeightBagProblem(wight, value, size) {const len = wight.length, dp = Array(size + 1).fill(0);for(let i = 1; i <= len; i++) {for(let j = size; j >= wight[i - 1]; j--) {dp[j] = Math.max(dp[j], value[i - 1] + dp[j - wight[i - 1]]);}}return dp[size];
}function test () {console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
}test();
416. 分割等和子集
第一想法
var canPartition = function (nums) {nums.sort((a, b) => a - b)console.log(nums);let l = nums[0];let sum = nums.reduce((x, y) => x + y)let r = sum - llet f = 1while (l <= r && f < nums.length) {if (l === r)return truel += nums[f]r = sum - lf++}f = 1l = nums[0] + nums[nums.length - 1]r = nums.reduce((x, y) => x + y) - lwhile (l <= r && f < nums.length / 2) {if (l === r)return truel += nums[f] + nums[nums.length - 1 - f]r = sum - lf++}return false
};
在这上面完了[1,2,3,4,5,6,7],应该还有回溯可以做
思想(带入背包)https://programmercarl.com/0416.%E5%88%86%E5%89%B2%E7%AD%89%E5%92%8C%E5%AD%90%E9%9B%86.html#%E6%80%9D%E8%B7%AF
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
/*** @param {number[]} nums* @return {boolean}*/
var canPartition = function(nums) {let target=nums.reduce((x,y)=>x+y)/2
const dp = Array(sum / 2 + 1).fill(0);
// 开始 01背包
for(let i = 0; i < nums.length; i++) {for(let j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历dp[j] = dp[j]> dp[j - nums[i]] + nums[i]? dp[j]:dp[j - nums[i]] + nums[i]if(dp[j]===target)return true}
}
return false
};