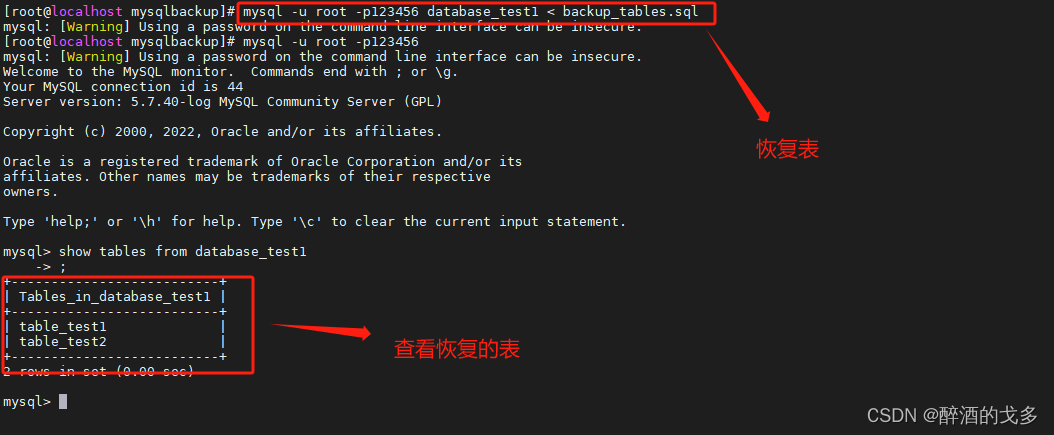
LeetCode原题链接：盛水最多的容器

下面是题目描述：
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。
示例1：
输入：[1,8,6,2,5,4,8,3,7]
输出：49

示例1图：

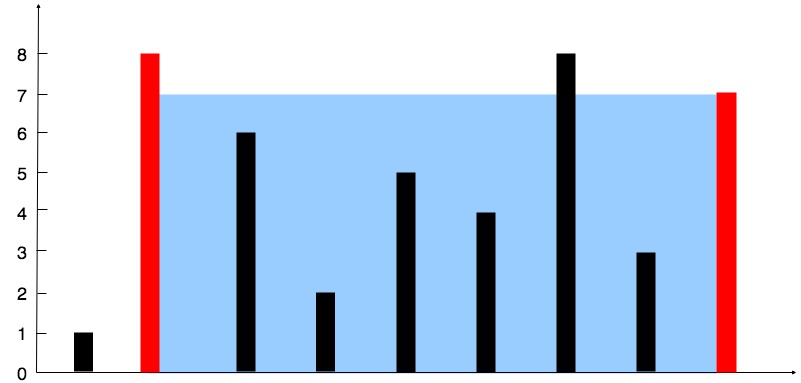
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：
输入：height = [1,1]
输出：1

提示：
n == height.length
2 <= n <= 10⁵
0 <= height[i] <= 10⁴

1、解题思路：
求解本题当然也可暴力枚举，但本文主要通过这道题进行双指针算法的学习，故这里直接进行双指针算法的讲解。

虽说是双指针，但求解本题更重要的是对其单调性规律的发现和运用：

首先，明确体积的计算为V = w * h，w是数组中两个数据的距离，h是这两数据中较小的一个（木桶效应，也是解出本题的关键）；

接下来关键点来了，此时 “固定” 较小的h，而将h中较大的向内枚举，也就是让w减小；那么枚举的过程有且仅有以下两种情况：
（1）w减小了，新的h比原来那个较小的h大，此时据木桶效应，仍以原来那个较小的h为计算体积的h；故此时计算V = w * h，w减小，h不变，V一定减小；
（2）w减小了，新的h比原来那个较小的h小，此时据木桶效应，以新的较小的h为计算体积的h；故此时计算V = w * h，w减小，h减小，V一定减小；

以上就前面所说的单调性规律，接下来的问题就是如何利用这个规律，通过双指针进行枚举解答

那么这里通过示例1 数组height [1,8,6,2,5,4,8,3,7] 进行说明：

这里的双指针更具体来说是对撞指针，所以让一个指针指向数组的第一个数据（设指针为front，下标为0），另一个指针指向最后一个数据（设指针为back，下标为7）开始枚举
（1）初始时，可得宽度为w = back - front；h取较小者，也就是height[front]；将它们相乘得到一个体积值V1；根据单调性，下一步若将back向前（向内）移进行枚举，直至第一个数据，算出来的体积一定都小于V1，（w一直在减小，h要么不变要么更小），故此时不应让back向前，而应让front向后（向内）移动进行枚举。

虽然front向后宽度也一定是减小的，但h有可能变大，且变大的幅度远超w减小的幅度而让总体积增大。

此时我们就可以得到两个指针移动的规律了：让高度小的指针向内移动枚举，即若front对应在数组中的数据大于等于back在数组中的数据，即height[front] >= height[back] ，就让back--；反之，则让front++；

（2）通过上面的分析，下一步是front++，++后我们计算出第二个体积V2；然后重复上述过程，每一步都能算出一个体积，最后这些体积中最大的即为问题的解。

2、具体代码：

int maxArea(vector<int>& height) {int front = 0;int back = height.size() - 1;int resArea = 0;while(front != back){int area = (back - front) * (height[front] < height[back] ? height[front] : height[back]);if(area > resArea){resArea = area;}if(height[front] < height[back]){front++;}else{back--;            }}return resArea;}

看完觉得有觉得帮助的话不妨点赞收藏鼓励一下，有疑问或看不懂的地方或有可优化的部分还恳请朋友们留个评论，多多指点，谢谢朋友们！🌹🌹🌹