目录
堆的基本存储
一、概念及其介绍
二、适用说明
三、结构图示
堆的 shift up
堆的 shift down
基础堆排序
一、概念及其介绍
二、适用说明
三、过程图示
优化堆排序
索引堆及其优化
一、概念及其介绍
二、适用说明
三、结构图示
堆的基本存储
一、概念及其介绍
堆(Heap)是计算机科学中一类特殊的数据结构的统称。
堆通常是一个可以被看做一棵完全二叉树的数组对象。
堆满足下列性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值。
- 堆总是一棵完全二叉树。
二、适用说明
堆是利用完全二叉树的结构来维护一组数据,然后进行相关操作,一般的操作进行一次的时间复杂度在 O(1)~O(logn) 之间,堆通常用于动态分配和释放程序所使用的对象。
若为优先队列的使用场景,普通数组或者顺序数组,最差情况为 O(n^2),堆这种数据结构也可以提高入队和出队的效率。
| 入队 | 出队 | |
|---|---|---|
| 普通数组 | O(1) | O(n) |
| 顺序数组 | O(n) | O(1) |
| 堆 | O(logn) | O(log) |
三、结构图示
二叉堆是一颗完全二叉树,且堆中某个节点的值总是不大于其父节点的值,该完全二叉树的深度为 k,除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大个数,第k 层所有的结点都连续集中在最左边。
其中堆的根节点最大称为最大堆,如下图所示:

我们可以使用数组存储二叉堆,右边的标号是数组的索引。
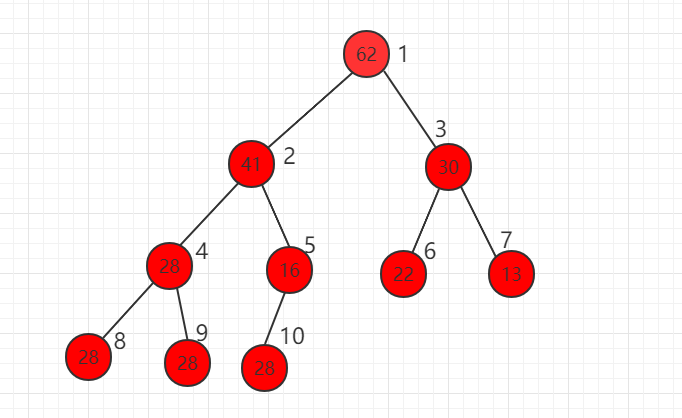
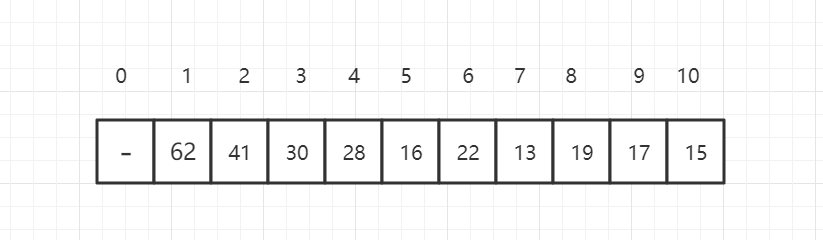
假设当前元素的索引位置为 i,可以得到规律:
parent(i) = i/2(取整)
left child(i) = 2*i
right child(i) = 2*i +1堆的 shift up
本小节介绍如何向一个最大堆中添加元素,称为 shift up。
假设我们对下面的最大堆新加入一个元素52,放在数组的最后一位,52大于父节点16,此时不满足堆的定义,需要进行调整。
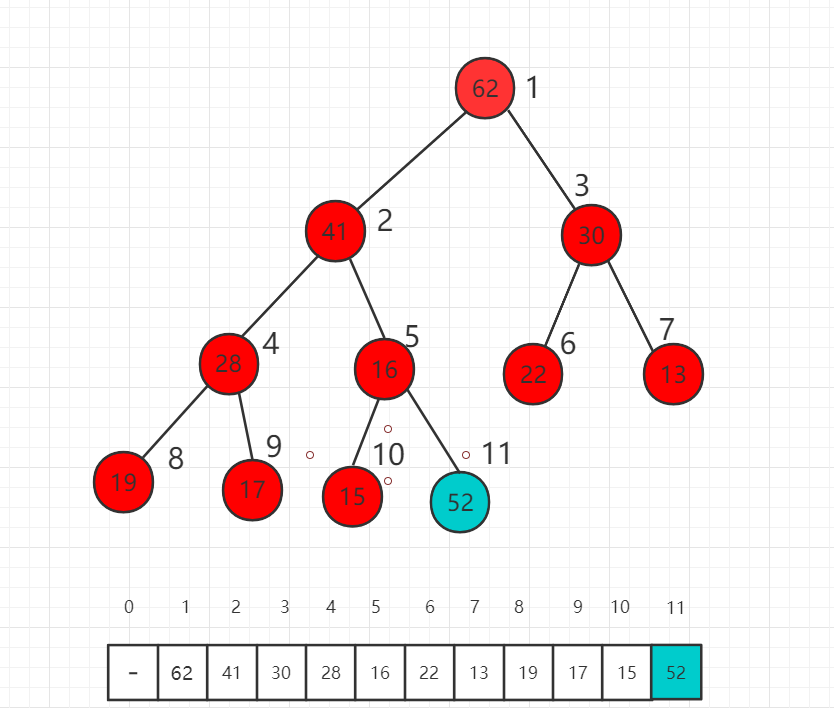
首先交换索引为 5 和 11 数组中数值的位置,也就是 52 和 16 交换位置。
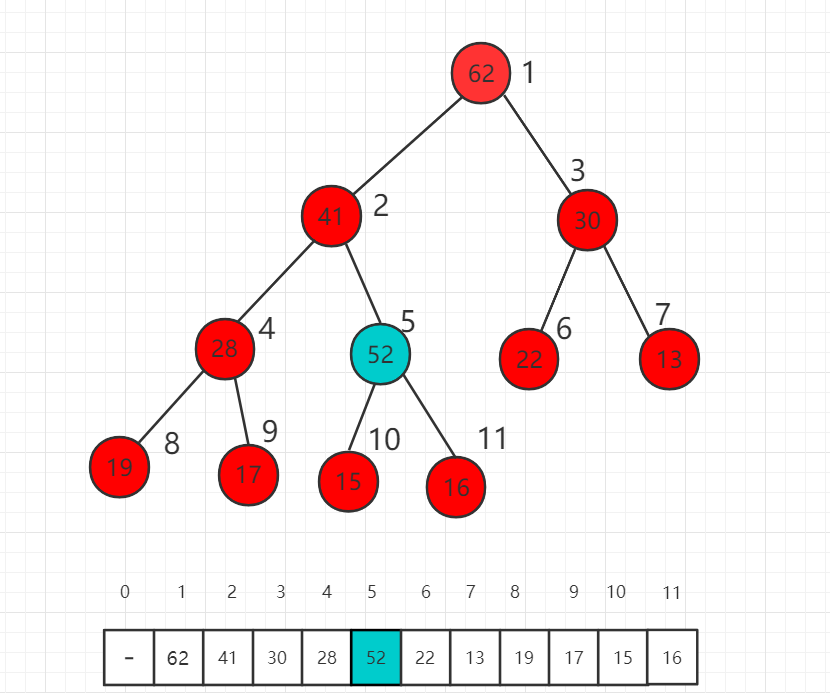
此时 52 依然比父节点索引为 2 的数值 41 大,我们还需要进一步挪位置。
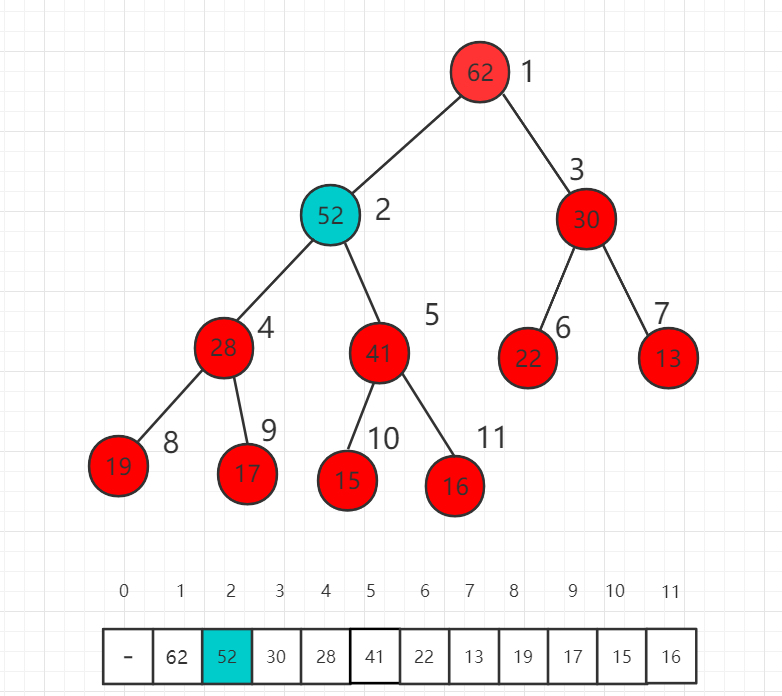
这时比较 52 和 62 的大小,52 已经比父节点小了,不需要再上升了,满足最大堆的定义。我们称这个过程为最大堆的 shift up。
堆的 shift down
本小节将介绍如何从一个最大堆中取出一个元素,称为 shift down,只能取出最大优先级的元素,也就是根节点,把原来的 62 取出后,下面介绍如何填补这个最大堆。
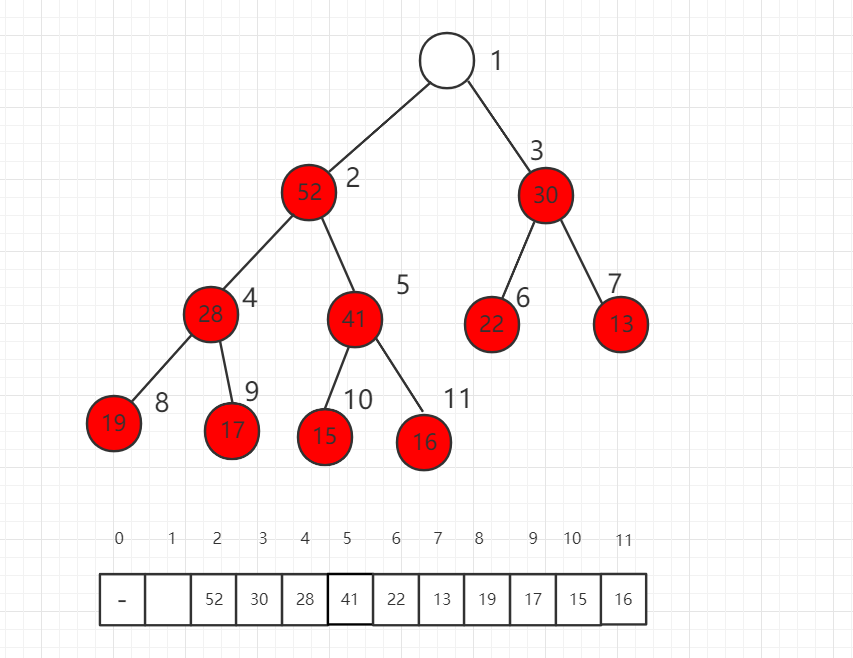
第一步,我们将数组最后一位数组放到根节点,此时不满足最大堆的定义。
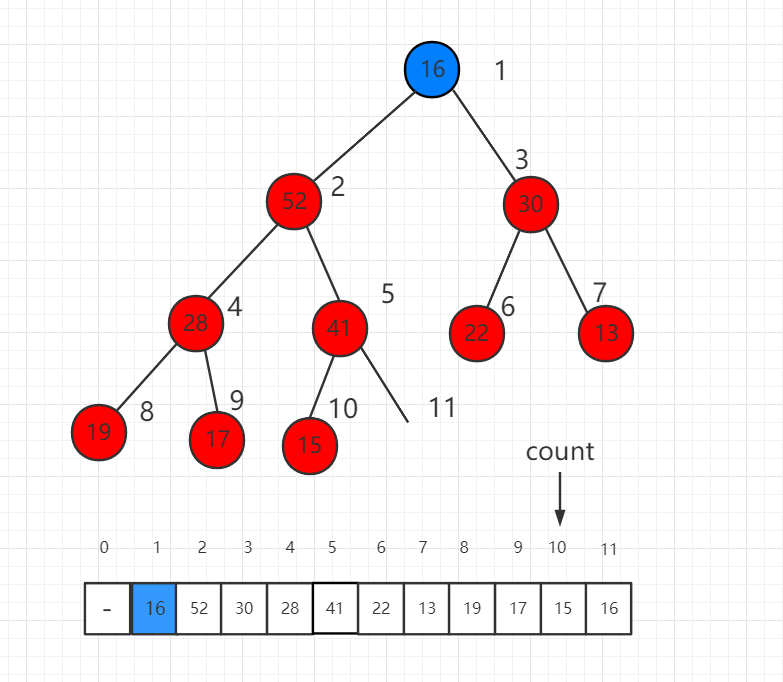
调整的过程是将这个根节点 16 一步一步向下挪,16 比子节点都小,先比较子节点 52 和 30 哪个大,和大的交换位置。
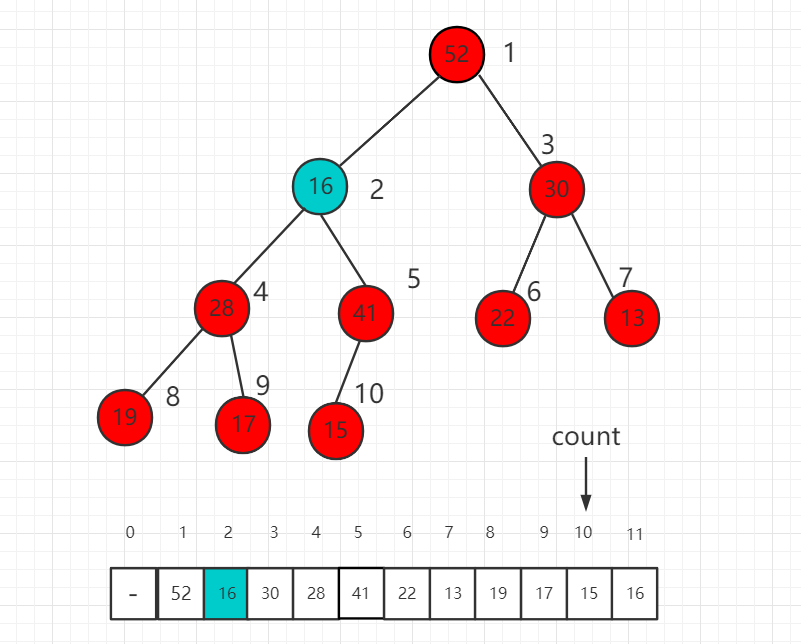
继续比较 16 的子节点 28 和 41,41 大,所以 16 和 41 交换位置。

继续 16 和孩子节点 15 进行比较,16 大,所以现在不需要进行交换,最后我们的 shift down 操作完成,维持了一个最大堆的性质。
基础堆排序
一、概念及其介绍
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。
堆是一个近似 完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
二、适用说明
我们之前构造堆的过程是一个个数据调用 insert 方法使用 shift up 逐个插入到堆中,这个算法的时候时间复杂度是 O(nlogn),本小节介绍的一种构造堆排序的过程,称为 Heapify,算法时间复杂度为 O(n)。
三、过程图示
完全二叉树有个重要性质,对于第一个非叶子节点的索引是 n/2 取整数得到的索引值,其中 n 是元素个数(前提是数组索引从 1 开始计算)。
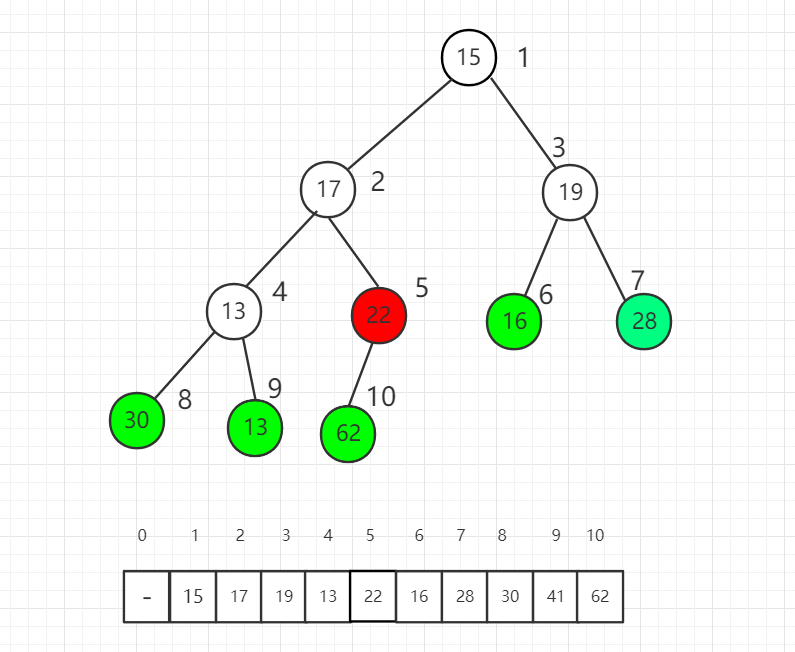
索引 5 位置是第一个非叶子节点,我们从它开始逐一向前分别把每个元素作为根节点进行 shift down 操作满足最大堆的性质。
索引 5 位置进行 shift down 操作后,22 和 62 交换位置。

对索引 4 元素进行 shift down 操作

对索引 3 元素进行 shift down 操作
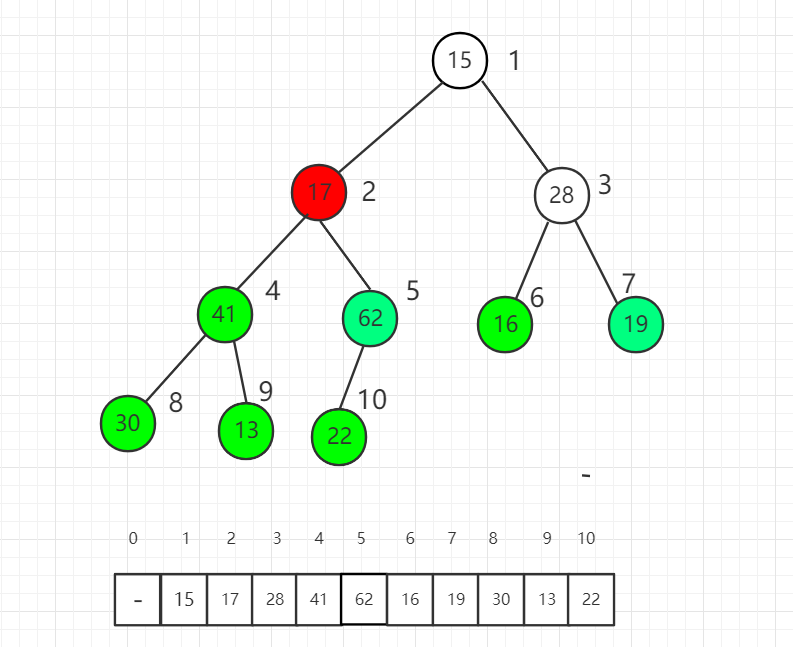
对索引 2 元素进行 shift down 操作
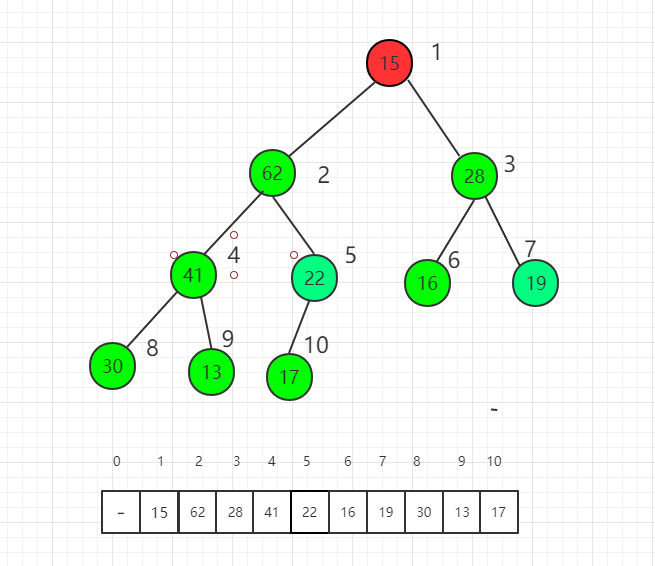
最后对根节点进行 shift down 操作,整个堆排序过程就完成了。

优化堆排序
上一节的堆排序,我们开辟了额外的空间进行构造堆和对堆进行排序。这一小节,我们进行优化,使用原地堆排序。
对于一个最大堆,首先将开始位置数据和数组末尾数值进行交换,那么数组末尾就是最大元素,然后再对W元素进行 shift down 操作,重新生成最大堆,然后将新生成的最大数和整个数组倒数第二位置进行交换,此时倒数第二位置就是倒数第二大数据,这个过程以此类推。
整个过程可以用如下图表示:

索引堆及其优化
一、概念及其介绍
索引堆是对堆这个数据结构的优化。
索引堆使用了一个新的 int 类型的数组,用于存放索引信息。
相较于堆,优点如下:
- 优化了交换元素的消耗。
- 加入的数据位置固定,方便寻找。
二、适用说明
如果堆中存储的元素较大,那么进行交换就要消耗大量的时间,这个时候可以用索引堆的数据结构进行替代,堆中存储的是数组的索引,我们相应操作的是索引。
三、结构图示
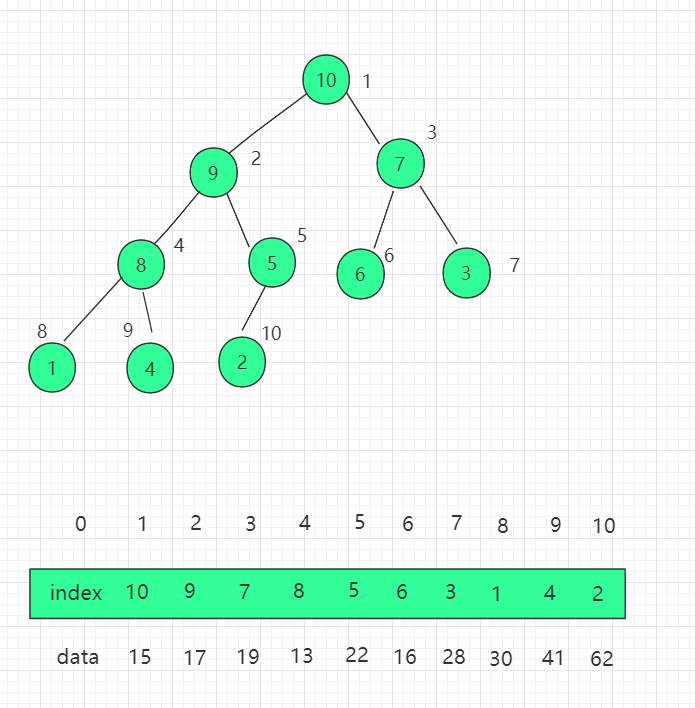
我们需要对之前堆的代码实现进行改造,换成直接操作索引的思维。首先构造函数添加索引数组属性 indexes。
protected T[] data; // 最大索引堆中的数据
protected int[] indexes; // 最大索引堆中的索引
protected int count;
protected int capacity;相应构造函数调整为,添加初始化索引数组。
...
public IndexMaxHeap(int capacity){data = (T[])new Comparable[capacity+1];indexes = new int[capacity+1];count = 0;this.capacity = capacity;
}
...调整插入操作,indexes 数组中添加的元素是真实 data 数组的索引 indexes[count+1] = i。
...
// 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
// 传入的i对用户而言,是从0索引的
public void insert(int i, Item item){assert count + 1 <= capacity;assert i + 1 >= 1 && i + 1 <= capacity;i += 1;data[i] = item;indexes[count+1] = i;count ++;shiftUp(count);
}
...调整 shift up 操作:比较的是 data 数组中父节点数据的大小,所以需要表示为 data[index[k/2]] < data[indexs[k]],交换 index 数组的索引,对 data 数组不产生任何变动,shift down 同理。
...
//k是堆的索引
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
private void shiftUp(int k){while( k > 1 && data[indexes[k/2]].compareTo(data[indexes[k]]) < 0 ){swapIndexes(k, k/2);k /= 2;}
}
...从索引堆中取出元素,对大元素为根元素 data[index[1]] 中的数据,然后再交换索引位置进行 shift down 操作。
...
public T extractMax(){assert count > 0;T ret = data[indexes[1]];swapIndexes( 1 , count );count --;shiftDown(1);return ret;
}
...也可以直接取出最大值的 data 数组索引值
...
// 从最大索引堆中取出堆顶元素的索引
public int extractMaxIndex(){assert count > 0;int ret = indexes[1] - 1;swapIndexes( 1 , count );count --;shiftDown(1);return ret;
}
...修改索引位置数据
...
// 将最大索引堆中索引为i的元素修改为newItem
public void change( int i , Item newItem ){i += 1;data[i] = newItem;// 找到indexes[j] = i, j表示data[i]在堆中的位置// 之后shiftUp(j), 再shiftDown(j)for( int j = 1 ; j <= count ; j ++ )if( indexes[j] == i ){shiftUp(j);shiftDown(j);return;}
}
...