AVL树【C++】

文章目录

AVL树结点的定义

AVL树中的结点定义为三叉链结构，并在每个结点当中引入平衡因子（右子树高度-左子树高度）

template<class K ,class V>
struct AVLTreeNode
{//三叉链AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;//	存储键值对 pair<K, V> _kv;//平衡因子int  _bf;AVLTreeNode(  const pair<K,V> kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0) //一开始左右子树为空树，平衡因子为0{}
};

Insert

	bool Insert(const pair<K,V> kv){//1、找到待插入位置//空树 if (_root == nullptr){_root = new Node(kv);return  true;}//不是空树 Node* parent = nullptr;Node* cur = _root;while (cur!= nullptr){//待插入结点的key值 < 当前结点的key值if (cur->_kv.first > kv.first){//往左子树找parent = cur;cur = cur->_left;}//	待插入结点的key值 > 当前结点的key值else if (cur->_kv.first < kv.first){//往右子树找 parent = cur;cur = cur->_right;}else//相等{return false;}}//将待插入节点插入到树中 cur = new Node(kv);//???if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//更新平衡因子,如果出现不平衡，就进行旋转while (parent !=nullptr) //最坏更新到根节点{//parent的左子树增高if (cur == parent->_left){parent->_bf--;}else //cur == _parent->_right//parent的右子树增高{parent->_bf++;}//结束平衡if (parent->_bf == 0){break;}else if (parent->_bf ==1|| parent->_bf == -1){//继续向上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//子树已经不平衡了，旋转保持平衡//左单旋if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);break;}//右单旋else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);break;}	//右左单旋else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);break;}//左右单旋if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);break;}}else{assert(false);}}return true;}

1、找到待插入位置。

待插入结点的key值<当前结点, 就插入到该结点的左子树。
待插入结点的key值>当前结点, 就插入到该结点的右子树。
待插入结点的key值==当前结点的key值 ,就插入失败。

2、找到待插入位置后，将待插入结点插入到树中。
3、更新平衡因子，如果出现不平衡，则需要进行旋转

平衡因子的更新：
一个结点的平衡因子是否需要更新，是看该结点的左右子树的高度有没有发生变化，因此插入一个结点后，该结点的祖先结点的平衡因子可能需要更新。
在这里插入图片描述

插入结点后需要倒着往上更新平衡因子：
1、新增结点在parent的右边，parent的平衡因子+ +
在这里插入图片描述

2、新增结点在parent的左边，parent的平衡因子− −
在这里插入图片描述

每更新完一个结点的平衡因子后：有以下几种情况需要注意

更新后parent平衡因子== 1or-1，说明parent所在的子树的高度变化，会再影响祖先，需要继续沿着到root的路径往上更新

更新后parent平衡因子==0，说明parent所在的子树的高度不变，不会再影响祖先，不用再继续沿着到根节点的路径往上更新

更新后parent平衡因子==2 or -2，说明parent所在的子树的高度变化且不平衡，对parent所在子树进行旋转，让他平衡

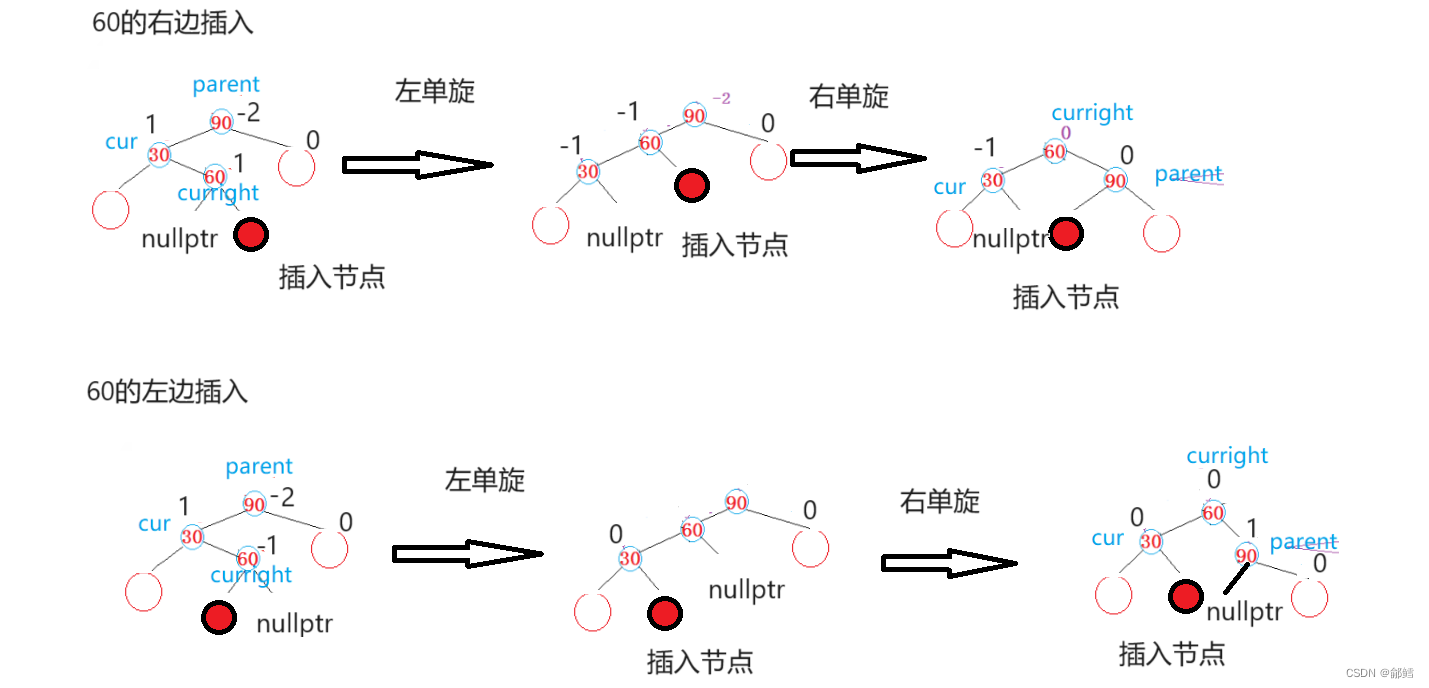
最坏情况下，更新平衡因子会一路更新到根结点。例如：
在这里插入图片描述

插入结点后需要倒着往上进行平衡因子的更新，所以我们将AVL树结点的结构设置为了三叉链结构，这样可以通过父指针找到其父结点，进而对其平衡因子进行更新。

cur(插入结点),parent(cur的父节点)
结论：当parent的平衡因子为-2/2时，cur的平衡因子必定是-1/1而不会是0

左单旋

在这里插入图片描述
1、让subR的左子树作为parent的右子树。
subR的左子树中结点的值 > parent的值，因此可以作为parent的右子树。

2、让parent作为subR的左子树。
parent结点的值和parent的左子树中结点的值 < subR的值，因此可以作为subR的左子树。

3、让subR作为整个子树的根。

4、更新平衡因子。

在这里插入图片描述
经过左单旋后，树的高度变为插入之前了，即树的高度没有发生变化，所以左单旋后无需继续往上更新平衡因子。

分析h可能的取值：
插入之前：a, b ,c是符合AVL规则的子树
当h（树的高度）为0时
在这里插入图片描述

当h（树的高度）为1时
在这里插入图片描述

当h（树的高度）为2时，a,b就是x,y,z中任意一种类型 ，c一定是z的类型

在这里插入图片描述
为什么c一定是z的类型？
如果c是y类型 ，新插入节点在左边可能不需要旋转
在这里插入图片描述

举几个实例：
在这里插入图片描述

	//左单旋 void RotateL(Node * parent ){//保持搜索树 //变成平衡树且降低树的高度 Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft!=nullptr){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;//如果parent不是一个子树 ，即parent就是根节点 if (parent == _root){_root = cur;cur->_parent = nullptr;}else//如果parent 是一个子树 {if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}//修改平衡因子 parent->_bf = cur->_bf = 0;}

右单旋

模型步骤：
1、让subL的右子树作为parent的左子树。

subL的右子树当中结点的值 < parent的值，因此可以作为parent的左子树。

2、让parent作为subL的右子树。
parent及其右子树当中结点的值 > subL的值，因此可以作为subL的右子树。

3、让subL作为整个子树的根。

4、更新平衡因子。
在这里插入图片描述

经过右单旋后，树的高度变为插入之前了，即树的高度没有发生变化，所以右单旋后无需继续往上更新平衡因子。

	//右单旋void RotateR(Node* parent){Node * cur = parent->_left;Node * curright = cur->_right;//b作为60的左子树 parent->_left= curright;if (curright !=nullptr){curright->_parent = parent;}Node* ppnode = parent->_parent;//60作为30的右子树cur->_right = parent;parent->_parent = cur;//parent作为根节点if (ppnode == nullptr){//将cur改成根节点_root = cur;cur->_parent = nullptr;}else//parent不是根节点，作为一个子树{//将cur改成这个子树的根节点 if (ppnode->_left ==parent){ppnode->_left = cur ;cur->_parent = ppnode;}else//ppnode->_right ==parent{ppnode->_right = cur;cur->_parent = ppnode;}}parent->_bf = cur->_bf = 0;}

分析h可能的取值：
插入之前：a, b ,c是符合AVL规则的子树
当h（树的高度）为0时
在这里插入图片描述
当h（树的高度）为1时
在这里插入图片描述

当h（树的高度）为2时，b,c就是x,y,z中任意一种类型 ，a一定是z的类型
在这里插入图片描述

右左双旋

1、插入新结点。
在这里插入图片描述
2、以90为旋转点进行右单旋。
在这里插入图片描述

3、以30为旋转点进行左单旋。
在这里插入图片描述
步骤：
1、以subR（90）为旋转点进行右单旋。
2、以parent（30）为旋转点进行左单旋。
3、更新平衡因子。

	void RotateRL(Node* parent) //右左双旋{Node* cur = parent->_right;Node* curleft = cur->_left;//90为旋转点，进行右单旋RotateR(parent->_right);	//30为旋转点，进行左单旋RotateL(parent);//更新平衡因子int bf = curleft->_bf;//插入节点就是60if (bf == 0){curleft->_bf = 0;parent->_bf = 0;cur->_bf = 0;}//插入节点是60的右边else if(bf ==1){curleft->_bf = 0;parent->_bf = -1;cur->_bf = 0;}//插入节点是60的左边else if (bf==-1){curleft->_bf = 0;parent->_bf = 0;cur->_bf = 1;}else{assert(false);}}

分析h可能的取值：
插入之前：a, b ,c是符合AVL规则的子树

当h（树的高度）为0时

在这里插入图片描述

当h（树的高度）为1时，有两种情况：
1、插入节点是60的左边
2、插入节点是60的右边
区分关键：看60的平衡因子
在这里插入图片描述

当h（树的高度）为2时，a, d是x,y,z中任意一颗子树

在这里插入图片描述

右左双旋的本质：
60的左边给30的右边
60的右边给90的左边
60成了这棵树的根

左右双旋

1、插入新结点。
在这里插入图片描述

2、以30为旋转点进行左单旋。
在这里插入图片描述

3、以90为旋转点进行右单旋。
在这里插入图片描述

步骤：
1、以subL为旋转点进行左单旋。
2、以parent为旋转点进行右单旋。
3、更新平衡因子。

左右双旋后，实际上就是让subLR的左子树和右子树，分别作为subL和parent的右子树和左子树，再让subL和parent分别作为subLR的左右子树，最后让subLR作为整个子树的根（结合图理解）。

三种情况会引发双旋
在这里插入图片描述

1、60就是新增
在这里插入图片描述

2、b 或者c 插入

在这里插入图片描述

	void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;//30为旋转点，进行左单旋RotateL(cur);//90为旋转点，进行右单旋RotateR(parent);//更新平衡因子int bf = curright->_bf;//插入节点就是60if (bf == 0){cur->_bf = curright->_bf = parent->_bf = 0;}//插入节点是60的左边else if (bf == -1){curright->_bf = parent->_bf = 0;cur->_bf = 1;}//插入节点是60的右边else if (bf == 1){cur->_bf = curright->_bf = 0;parent->_bf = 1;}else{assert(false);}}

AVL树的验证

满足AVL，就满足 右子树-左子树的高度差 < 2 ,在该过程中我们可以检查每个结点当中平衡因子是否正确。

    int Height(Node *root){if (root == nullptr){return 0;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (leftHeight > rightHeight){return  leftHeight + 1;}else//(leftHeight <= rightHeight){return  rightHeight + 1;}}bool IsBalance(){return _IsBalance(_root);}bool _IsBalance(Node* root){if (root == nullptr){return true;}//左右子树高度差 < 2 int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if ( (rightHeight - leftHeight) != root->_bf){cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;return false;}else if (abs(rightHeight - leftHeight) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right) ){return true; }else { return false; }}

AVL树的性能

AVL树是一棵绝对平衡的二叉搜索树，其要求每个结点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即logN。但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。

因此，如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的（即不会改变），可以考虑AVL树，但当一个结构经常需要被修改时，AVL树就不太适合了。

完整代码

#include<iostream>
#include<map>
#include<vector>
#include<assert.h>
using namespace std;
template<class K ,class V>
struct AVLTreeNode
{//三叉链AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;//方便找到其父结点//	存储键值对 pair<K, V> _kv;//平衡因子int  _bf;AVLTreeNode(  const pair<K,V> kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0) //一开始左右子树为空树，平衡因子为0{}
};template <class K ,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K,V> kv){//1、找到待插入位置//空树 if (_root == nullptr){_root = new Node(kv);return  true;}//不是空树 Node* parent = nullptr;Node* cur = _root;while (cur!= nullptr){//待插入结点的key值 < 当前结点的key值if (cur->_kv.first > kv.first){//往左子树找parent = cur;cur = cur->_left;}//	待插入结点的key值 > 当前结点的key值else if (cur->_kv.first < kv.first){//往右子树找 parent = cur;cur = cur->_right;}else//相等{return false;}}//将待插入节点插入到树中 cur = new Node(kv);//???if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//更新平衡因子,如果出现不平衡，就进行旋转while (parent !=nullptr) //最坏更新到根节点{//parent的左子树增高if (cur == parent->_left){parent->_bf--;}else //cur == _parent->_right//parent的右子树增高{parent->_bf++;}//结束平衡if (parent->_bf == 0){break;}else if (parent->_bf ==1|| parent->_bf == -1){//继续向上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//子树已经不平衡了，旋转保持平衡//左单旋if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);break;}//右单旋else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);break;}	//右左单旋else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);break;}//左右单旋if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);break;}}else{assert(false);}}return true;}//左单旋 void RotateL(Node * parent ){//保持搜索树 //变成平衡树且降低树的高度 Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft!=nullptr){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;//如果parent不是一个子树 ，即parent就是根节点 if (parent == _root){_root = cur;cur->_parent = nullptr;}else//如果parent 是一个子树 {if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}//修改平衡因子 parent->_bf = cur->_bf = 0;}//右单旋void RotateR(Node* parent){Node * cur = parent->_left;Node * curright = cur->_right;//b作为60的左子树 parent->_left= curright;if (curright !=nullptr){curright->_parent = parent;}Node* ppnode = parent->_parent;//60作为30的右子树cur->_right = parent;parent->_parent = cur;//parent作为根节点if (ppnode == nullptr){//将cur改成根节点_root = cur;cur->_parent = nullptr;}else//parent不是根节点，作为一个子树{//将cur改成这个子树的根节点 if (ppnode->_left ==parent){ppnode->_left = cur ;cur->_parent = ppnode;}else//ppnode->_right ==parent{ppnode->_right = cur;cur->_parent = ppnode;}}parent->_bf = cur->_bf = 0;}void RotateRL(Node* parent) //右左双旋{Node* cur = parent->_right;Node* curleft = cur->_left;//90为旋转点，进行右单旋RotateR(parent->_right);	//30为旋转点，进行左单旋RotateL(parent);//更新平衡因子int bf = curleft->_bf;//插入节点就是60if (bf == 0){curleft->_bf = 0;parent->_bf = 0;cur->_bf = 0;}//插入节点是60的右边else if(bf ==1){curleft->_bf = 0;parent->_bf = -1;cur->_bf = 0;}//插入节点是60的左边else if (bf==-1){curleft->_bf = 0;parent->_bf = 0;cur->_bf = 1;}else{assert(false);}}void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;//30为旋转点，进行左单旋RotateL(cur);//90为旋转点，进行右单旋RotateR(parent);//更新平衡因子int bf = curright->_bf;//插入节点就是60if (bf == 0){cur->_bf = curright->_bf = parent->_bf = 0;}//插入节点是60的左边else if (bf == -1){curright->_bf = parent->_bf = 0;cur->_bf = 1;}//插入节点是60的右边else if (bf == 1){cur->_bf = curright->_bf = 0;parent->_bf = 1;}else{assert(false);}}int Height(Node *root){if (root == nullptr){return 0;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (leftHeight > rightHeight){return  leftHeight + 1;}else//(leftHeight <= rightHeight){return  rightHeight + 1;}}bool IsBalance(){return _IsBalance(_root);}bool _IsBalance(Node* root){if (root == nullptr){return true;}//左右子树高度差 < 2 int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if ( (rightHeight - leftHeight) != root->_bf){cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;return false;}else if (abs(rightHeight - leftHeight) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right) ){return true; }else { return false; }}
private:Node* _root =nullptr;
};

测试代码

#include"AVLTree.h"void Test1()
{AVLTree<int, int> t;int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };for (auto e : a){/*手动断点*/if (e == 7){int x = 10;//仅仅是为了打断点，空语句不能打断点}t.Insert(make_pair(e, e));//cout << "Insert ："<<e<<"->";////cout<< t.IsBalance();//cout << endl;cout << "Insert:" << e << "->" << t.IsBalance() << endl;}
}void Test2() //测试左单旋函数
{AVLTree<int, int> t;int a[] = { 30,60,90 };for (auto e : a){t.Insert(  make_pair(e,e) ) ;cout << "Insert:" << e << "->" << t.IsBalance() << endl;}}
int main()
{Test1();//Test2();return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/127291.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

openGauss学习笔记-92 openGauss 数据库管理-内存优化表MOT管理-内存表特性-使用MOT-MOT使用MOT SQL覆盖和限制

openGauss学习笔记-92 openGauss 数据库管理-内存优化表MOT管理-内存表特性-使用MOT-MOT使用MOT SQL覆盖和限制

文章目录 openGauss学习笔记-92 openGauss 数据库管理-内存优化表MOT管理-内存表特性-使用MOT-MOT使用MOT SQL覆盖和限制92.1 不支持的特性92.2 MOT限制92.3 不支持的DDL操作92.4 不支持的数据类型92.5 不支持的索引DDL和索引92.6 不支持的DML92.7 不支持的JIT功能&#xff08;…
阅读更多...
51单片机+EC11编码器实现可调参菜单+OLED屏幕显示

51单片机+EC11编码器实现可调参菜单+OLED屏幕显示

51单片机+EC11编码器实现可调参菜单+OLED屏幕显示 📍相关篇《stc单片机使用外部中断+EC11编码器实现计数功能》 🎈《STC单片机+EC11编码器实现调节PWM输出占空比》 🌼实际操作效果 🍁整个项目实现框架： 📓EC11接线原理图： 📓项目工程简介 📝仅凭借一个EC11编…
阅读更多...
【UE】在游戏运行时，通过选择uasset来生成静态网格体

【UE】在游戏运行时，通过选择uasset来生成静态网格体

目录 主要流程 步骤 一、创建用于包含静态网格体的Actor蓝图 二、按钮点击事件 效果 主要流程 用户点击按钮后产生一个文件对话框&#xff0c;用户通过文件对话框选择指定的文件夹&#xff0c;我们获取到这个文件夹路径后处理成“按路径获取资产”节点所需的输入&#x…
阅读更多...
【C++设计模式之组合模式:结构型】分析及示例

【C++设计模式之组合模式:结构型】分析及示例

简介 组合模式是一种结构型设计模式&#xff0c;它能够将对象组合成树形结构以表示“整体-部分”的层次结构&#xff0c;并且能够使用相同的方式处理单个对象和组合对象。组合模式使得客户端可以一致地处理单个对象和组合对象&#xff0c;无需关心具体的对象类型。 组合模式将对…
阅读更多...
回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测

回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测

回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测 目录 回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测预测效果基本介绍模型描述程序设计预测效果 <
阅读更多...
12.1 使用键盘鼠标监控钩子

12.1 使用键盘鼠标监控钩子

本节将介绍如何使用Windows API中的SetWindowsHookEx和RegisterHotKey函数来实现键盘鼠标的监控。这些函数可以用来设置全局钩子&#xff0c;通过对特定热键挂钩实现监控的效果&#xff0c;两者的区别在于SetWindowsHookEx函数可以对所有线程进行监控&#xff0c;包括其他进程中…
阅读更多...
手机投屏电脑软件AirServer5.6.3.0最新免费版本下载

手机投屏电脑软件AirServer5.6.3.0最新免费版本下载

随着智能手机的普及&#xff0c;越来越多的人喜欢用手机观看视频、玩游戏、办公等。但是&#xff0c;有时候手机屏幕太小&#xff0c;不够清晰&#xff0c;也不方便操作。这时候&#xff0c;如果能把手机屏幕投射到电脑上&#xff0c;就可以享受更大的视野&#xff0c;更流畅的…
阅读更多...
SpringMVC的视图

SpringMVC的视图

文章目录 1. ThymeleafView2. 转发视图3. 重定向视图4. 视图控制器view-controller5. 总结6. 荐书 SpringMVC中的视图是View接口&#xff0c;视图的作用渲染数据&#xff0c;将模型Model中的数据展示给用户SpringMVC视图的种类很多&#xff0c;默认有转发视图和重定向视图 当工…
阅读更多...
【Node.js】NPM 和 package.json

【Node.js】NPM 和 package.json

NPM npm 是 Node.js 的包管理工具&#xff0c;基于命令行&#xff0c;用于安装、升级、移除、管理依赖项。 常用命令&#xff1a; npm init&#xff1a;初始化一个新的 npm 项目&#xff0c;创建 package.json 文件。&#xff08;括号里为默认值&#xff09; description&am…
阅读更多...
如何保证 RabbitMQ 的消息可靠性？

如何保证 RabbitMQ 的消息可靠性？

项目开发中经常会使用消息队列来完成异步处理、应用解耦、流量控制等功能。虽然消息队列的出现解决了一些场景下的问题&#xff0c;但是同时也引出了一些问题&#xff0c;其中使用消息队列时如何保证消息的可靠性就是一个常见的问题。如果在项目中遇到需要保证消息一定被消费的…
阅读更多...
DRM全解析 —— CRTC详解（1）

DRM全解析 —— CRTC详解（1）

本文参考以下博文&#xff1a; Linux内核4.14版本——drm框架分析(4)——crtc分析 特此致谢&#xff01; 1. 简介 CRTC实际上可以拆分为CRTC。CRT的中文意思是阴极摄像管&#xff0c;就是当初老电视上普遍使用的显像管&#xff08;老电视之所以都很厚&#xff0c;就是因为它…
阅读更多...
最全解决docker配置kibana报错 Kibana server is not ready yet

最全解决docker配置kibana报错 Kibana server is not ready yet

问题复现&#xff1a; 在浏览器输入http://192.168.101.65:5601/ 访问kibana报错 Kibana server is not ready yet 问题报错&#xff1a; 首先查看kibana的日志 docker logs kibana 看到报错如下&#xff1a; {"type":"log","timestamp":&q…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023