一 BPF高级过滤条件
高级filter官方地址 常见需求案例汇总

过滤的目的:获取最'精细'、'准确'的数据思考: 抓取'更精确'的包?1) 'tcp/ip' 报文结构要'精通',这样才能知道如何获取自己'想要的信息' -> '偏移量'2) tcpdump 的'synax语法'要精通,要'正确写对'3) 多练习,任何东西不是'一蹴而就'的,保持好耐心,熟练如何抓取到更精确的包
① 多条件过滤规则组合

通过命令选项的不同组合 '使用 逻辑运算符' 完成'更复杂'的任务说明: 以下'两种'符号'通用'and: 所有的条件都需要满足,也可以表示为 '&&'or: 只要有一个条件满足就可以,也可以表示为 '||'not: 取反,也可以使用 '!'优先级: 取反操作有'最高'优先级,'或'操作和'and'操作有'相同'的优先级,运算时从'左到右'结合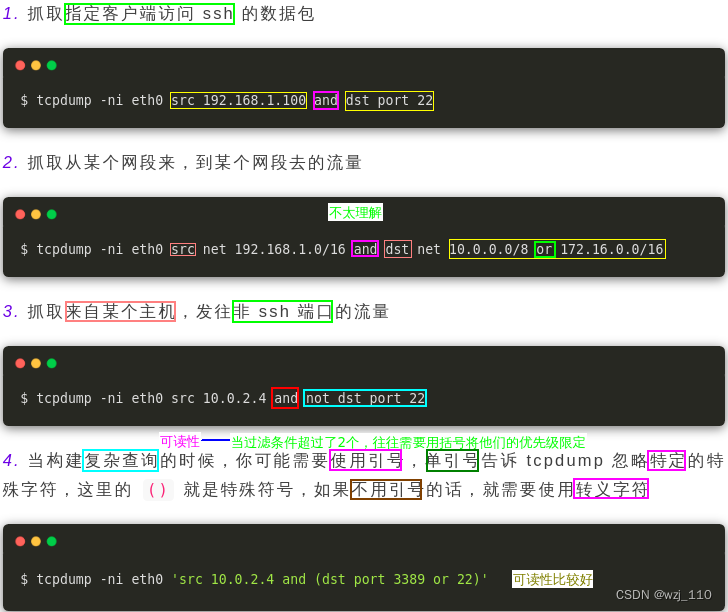
细节: 由于'()'在'tcpdump'和'shell'中都有特殊含义,避免被'shell'转义,需要加'\'推荐: 使用'()'、'单引号'增加'read 可读性'![]()
② 条件判断
=: 判断二者'相等'==: 判断二者'相等'!=: 判断二者'不相等'补充: '&'是位操作符、'>>'和'<<' 是移位操作符③ 基于包大小进行过滤


④ 根据 mac 地址进行过滤
其中 ehost 是记录在 /etc/ethertypes 里的 'name' --> '未验证'tcpdump ether host [ehost]tcpdump ether dst [ehost]tcpdump ether src [ehost]⑤ 数据包标志位
tcpdump 支持我们根据'数据包的标志位'进行过滤 --> 抓取'指定TCP标识位'的数据包语法: proto[expr:size]1) proto:可以是熟知的'协议之一' --> 如'ip',arp,'tcp',udp,'icmp',ipv6等强调: 并不'局限于'tcp[tcpflags]形式2) expr: 可以是'数值',也可以是一个'表达式',表示与'指定的协议头开始处'的字节'偏移量'补充: 还可以是'别名常量'形式强调: 后续需要充分理解'tcp/ip'协议簇才能理解和书写正确的'偏移量' --> '字节'3) size: 是'optional 可选'的,表示'从字节偏移量'开始取的'字节数量count'补充: 对于 'proto[expr:size] =z' 形式1) 当z为'一个'字节时,z为'10'进制2) 当z为'多'字节时,z为'16'进制,用'0x'开头⑥ tcp[13]由来
分析: 编号从'0'开始算,TCP'控制标志'位于13字节,分析编号'13'的字节强调: 需要理解'bytes'、'bit' 含义 --> 1 bytes = 8bit

TCP包里有个'flags字段'表示'包'的类型,tcpdump可以根据'该字段'抓取相应类型的包:tcp[13] 就是 TCP flags '(URG,ACK,PSH,RST,SYN,FIN)',按照这个计算标志位置位后的'数值'
tcp[tcpflags] '等价' tcp[13]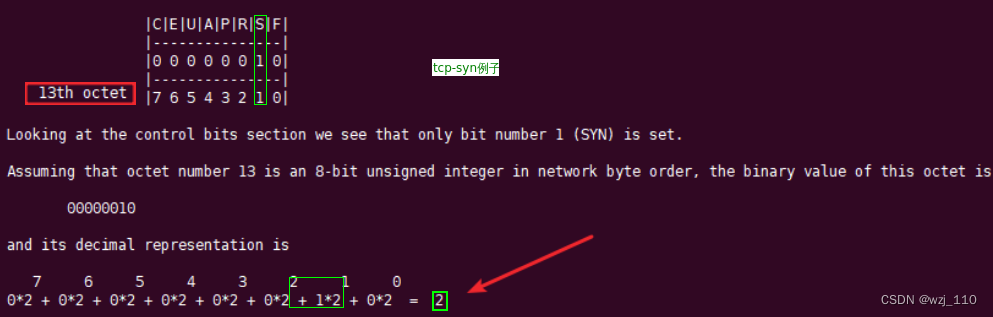
编号13的字节 tcp[13]详解
⑦ 根据 tcpflags 进行过滤
tcp-fin, tcp-syn, tcp-rst, tcp-push, tcp-ack, tcp-urg 可以理解为'别名常量'强调: 由于数字'不好记忆',所以一般使用这样的"别名常量"表示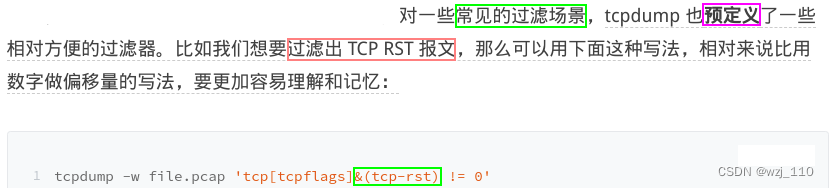
二进制'按位与'运算符& : 0&0=0; 0&1=0 1&1=1运算规则:如果两个二进制数的同一个位数上的数'都为1',则当前位'为1',否则为0+++++++++++ "分割线" +++++++++++补充: 全'数值'的形式,二者也可以'混合'使用tcpdump 'tcp[13] & 32!=0' 所有 URGENT ( URG ) 包tcpdump 'tcp[13] & 16!=0' 所有 ACKNOWLEDGE ( ACK ) 包tcpdump 'tcp[13] & 8!=0' 所有 PUSH ( PSH ) 包tcpdump 'tcp[13] & 4!=0' 所有 RESET ( RST ) 包tcpdump 'tcp[13] & 2!=0' 所有 SYNCHRONIZE ( SYN ) 包tcpdump 'tcp[13] & 1!=0' 所有 FINISH ( FIN ) 包tcpdump 'tcp[13]=18' 所有 SYNCHRONIZE/ACKNOWLEDGE ( SYNACK ) 包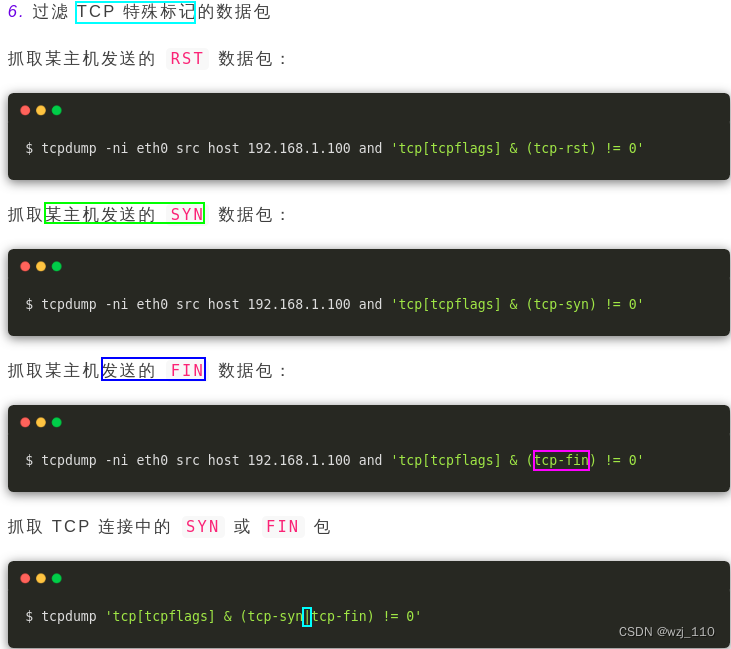
⑧ 其它高级