目录
蛮力法
分治法
探究分治规模小于一定程度时采用暴力解法
蛮力法
- 算法思想
蛮力法,顾名思义,即穷举所有点与点之间的距离,两层循环暴力找出最近点对。算法执行可视化如图1所示,word文档GIF静态显示,附件已含动图。
 图1
图1
- 伪代码

matlab代码
result=[];
for power=1:10scale=power*100000;count=0;for times=1:20x=randi(scale,1,scale);y=randi(scale,1,scale);tic;[i,j]=brute(x,y,scale);count=count+toc; endcount=count/20;result=[result,count];
end
function [mini,minj]=brute(x,y,scale)mini=1;minj=1;minDistance=Inf;for i=1:scale-1for j=1:scaleif i==jbreakenddistance=(x(i)-x(j))^2+(y(i)-y(j))^2;if distance<minDistancemini=i;minj=j;minDistance=distance;endendend
end- 实验结果
环境为MATLAB,数据规模为1w到5w,运行结果如图2所示。
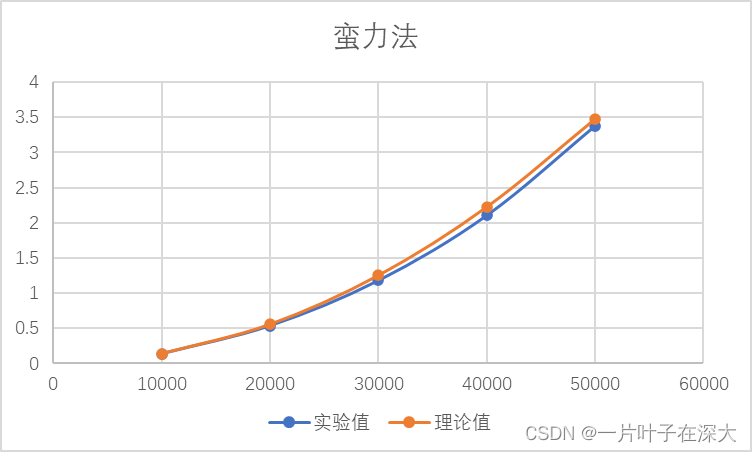
图2
具体数据如表1所示。
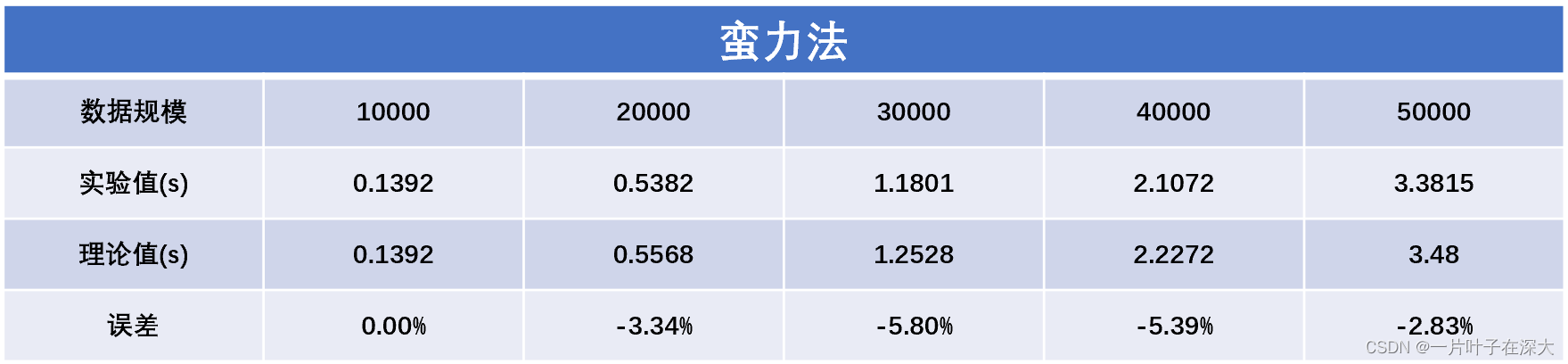
表1
分析:
由实验结果可知,蛮力法的实验值与理论值基本一致,算法的时间复杂度确实为O(n2),确实很慢。
分治法
- 算法思想
先对点进行预处理按横坐标排序,然后每次将点均分成左右两个子集,最短距离的两个点要么都在左子集,要么都在右子集,要么一个点在左子集中,一个点在右子集中,对于前面两种情况,问题变成递归寻找子集的最短距离,算法执行可视化如图3所示,word文档GIF静态显示,附件已含动图。
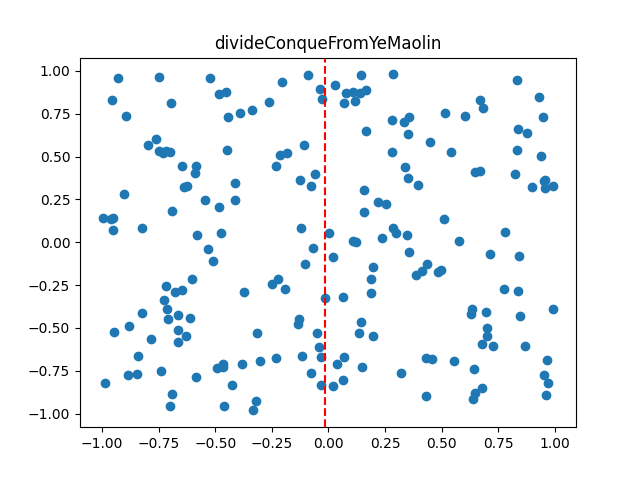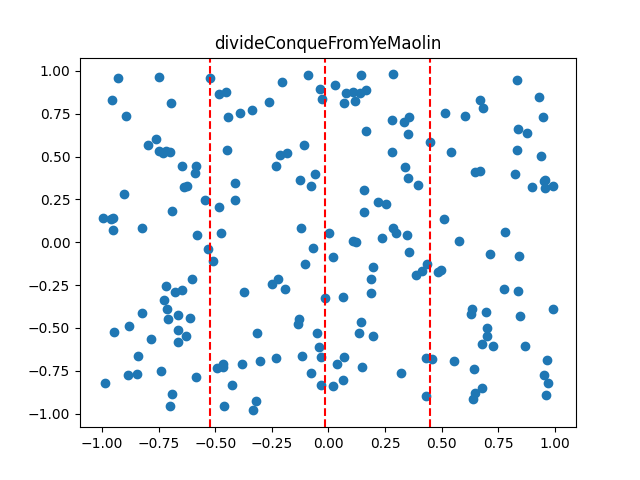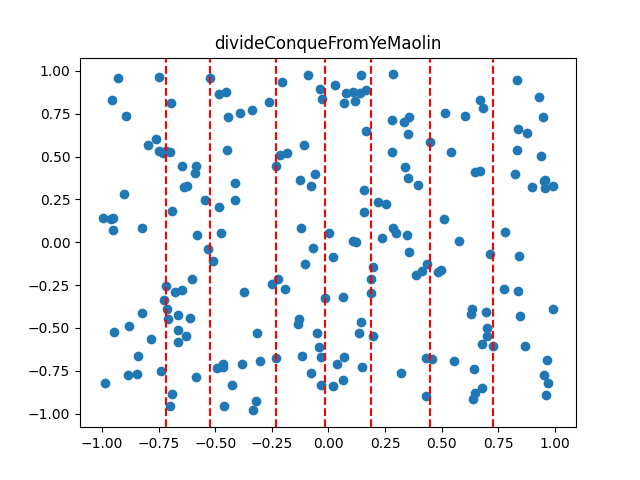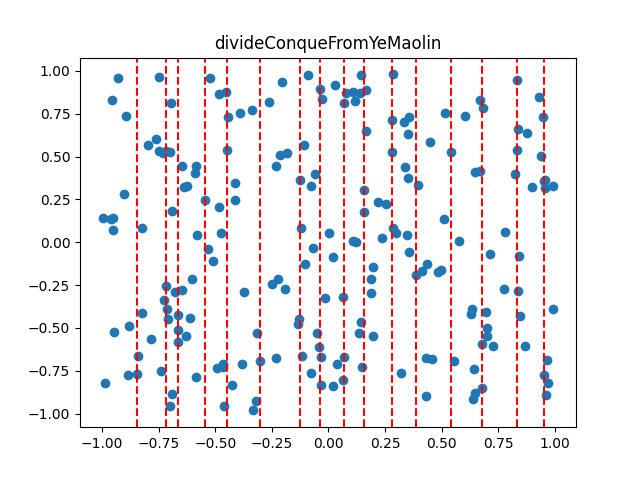
图3
而对于跨越中间线的情况,由左右两个子集可以算出一个目前最短距离minDistance,然后将距离中间点的距离小于minDistance的点找出来,如图4所示。

图4
如果存在最短距离,那么一定是一边一个点,所以我们需要将两边点的距离算一下,实际上,我们需要对于一边的点,我们需要计算距离的点最多不超过4个,因为同一边的点与点之间的距离肯定大于等于minDistance,所以对于另一边的点来说,范围小于minDistance内的点不会超过4个,如图5所示。
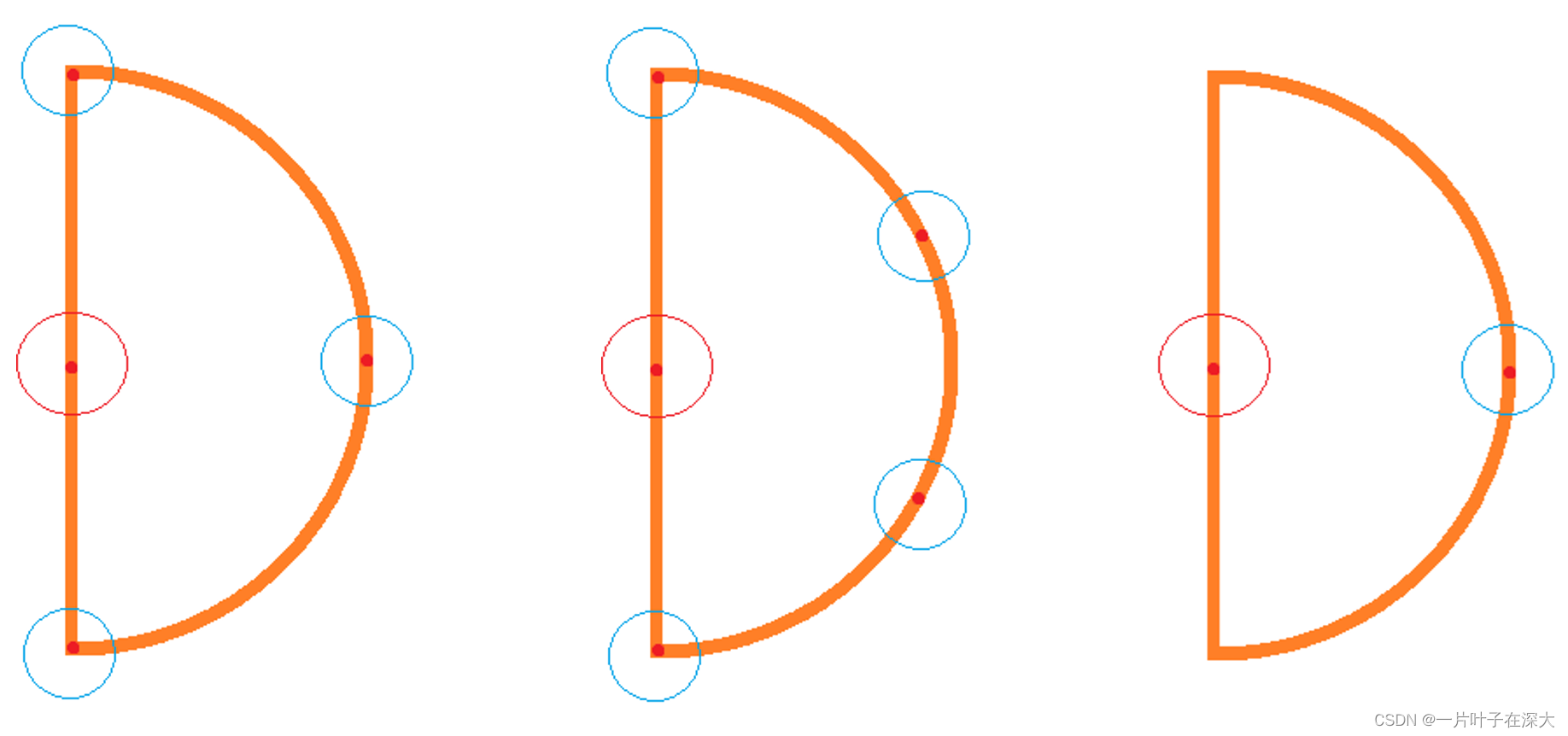
图5
- 伪代码

matlab代
result=[];
for power=1:10scale=power*100000;count=0;for times=1:20x=randi(scale,1,scale);y=randi(scale,1,scale);tic;[x,y]=Quick(1,scale,x,y);[mini,minj,minDistance]=divide(x,y,scale);count=count+toc; endcount=count/20;result=[result,count];
end
function [mini,minj,minDistance]=brute(x,y,scale)mini=1;minj=2;minDistance=Inf;for i=1:scale-1for j=i+1:scaledistance=(x(i)-x(j))^2+(y(i)-y(j))^2;if distance<minDistancemini=i;minj=j;minDistance=distance;endendend
end
function [mini,minj,minDistance]=divide(x,y,scale)if length(x)<3[mini,minj,minDistance]=brute(x,y,scale);return;endhalf=floor(scale/2);[i,j,minLeft]=divide(x(1:half),y(1:half),half);[ii,jj,minRight]=divide(x(half+1:scale),y(half+1:scale),scale-half);if minLeft<minRightminDistance=minLeft;mini=i;minj=j;elseminDistance=minRight;mini=ii;minj=jj;endleft=[];right=[];for i=half-1:-1:1if abs(x(i)-x(half))>=sqrt(minDistance)breakendleft=[left,i];endfor i=half+1:scaleif abs(x(i)-x(half))>=sqrt(minDistance)breakendright=[right,i];endfor i=1:length(left)for j=1:length(right)if j>3breakenddistance=(x(left(i))-x(right(j)))^2+(y(left(i))-y(right(j)))^2;if distance<minDistancemini=left(i);minj=right(j);minDistance=distance;endendendfor i=1:length(right)for j=1:length(left)if j>3breakenddistance=(x(left(j))-x(right(i)))^2+(y(left(j))-y(right(i)))^2;if distance<minDistancemini=left(j);minj=right(i);minDistance=distance;endendend
end
function[x,y]=Quick(low,high,x,y)i=low;j=high;pivot=x(low);temp=y(low);while low<highwhile low<high&&pivot<=x(high)high=high-1;endif low<highx(low)=x(high);y(low)=y(high);low=low+1;endwhile low<high&&pivot>x(low)low=low+1;endif low<highx(high)=x(low);y(high)=y(low);high=high-1;endendx(low)=pivot;y(low)=temp;if i<low-1[x,y]=Quick(i,low-1,x,y);endif high+1<j[x,y]=Quick(high+1,j,x,y);end
end- 算法复杂度
对于数据规模为n的情况,二分的次数为log2n次,而计算跨中间线距离的时候计算次数小于3n,即此处的时间复杂度是线性的,即T(n)=T(n/2)+O(n),可算得T(n)=nlogn。
- 实验结果
先在小规模数据上跑,环境为MATLAB,数据规模为1w到5w,运行结果如图6所示。

图6
具体数据如表2所示。
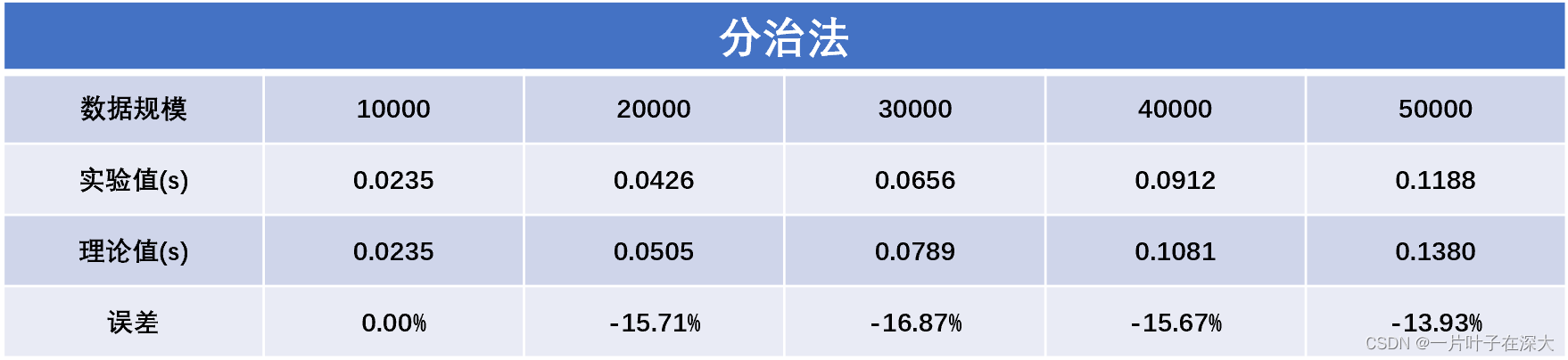
表2
数据规模为10w到100w,运行结果如图7所示。
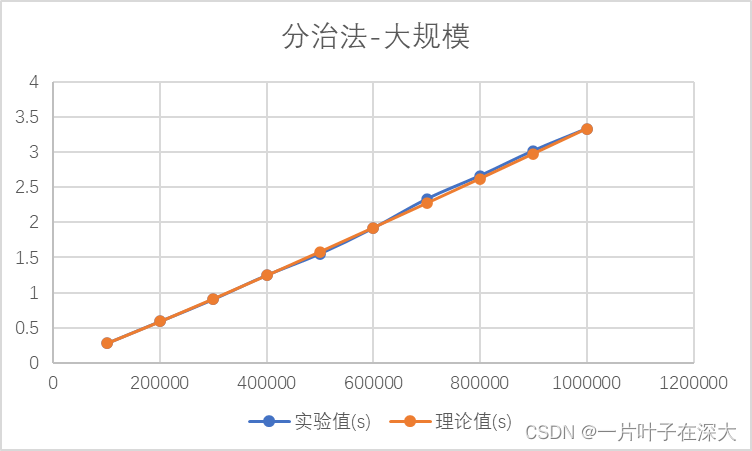
图7
具体数据如表3所示。

表3
分析:
由实验结果可知,分治法明显远远快于蛮力法,小规模数据时实验值略小于理论值,大规模时实验值与理论值基本一致。
探究分治规模小于一定程度时采用暴力解法
由于分治时不断递归调用函数,程序开销较大,考虑当分治到数据规模小于一定程度时采用暴力解法的运行效果,数据规模为1w,参数设置100到1000测试,结果如图8所示。

图8
由实验结果可知,分治规模达到200时使用暴力效果最佳,将参数设置为200,在数据规模为1w到5w上与原始分治法对比,如图9所示。

图9
在数据规模为10w到100w上与原始分治法对比,如图10所示。
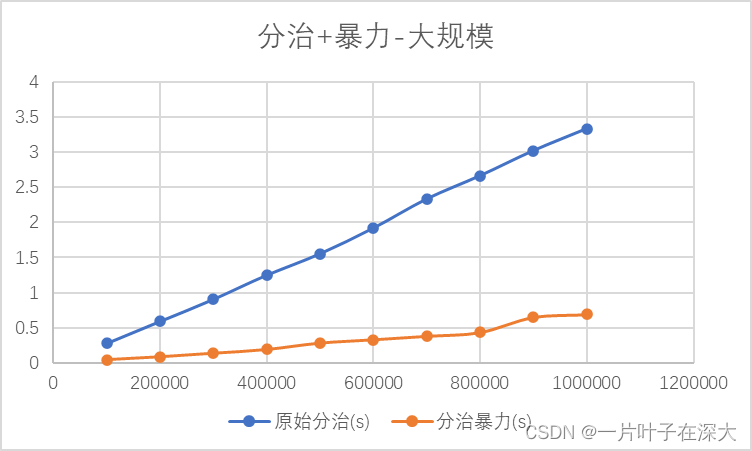
图10
分析:
由实验结果可知,在分治规模小于一定数量时采用暴力求解效率更快,特别是在数据规模大的时候,这种暴力分治相结合的方法相比原始分治法具有很大的优势。