同样很多收敛性的证明不是重点,但里面的知识还是需要适当掌握,知道中间的大致思考和解决路径即可。

 本质还是极限的可交换性,求导可以换到积分里面去操作。
本质还是极限的可交换性,求导可以换到积分里面去操作。
这里要注意变量的区别,首先积分的被积变量是x,但是函数的变量是y,y是参数,所以叫做带参数的积分。

这是一个很有意思的题,首先我们不好求积分的时候,可以先对里面的参变量进行求导。得到一个简单的式子,然后再积分即可。
 这是积分的可交换性。
这是积分的可交换性。

要反常积分收敛,就是说要在无界的部分,积分足够小。
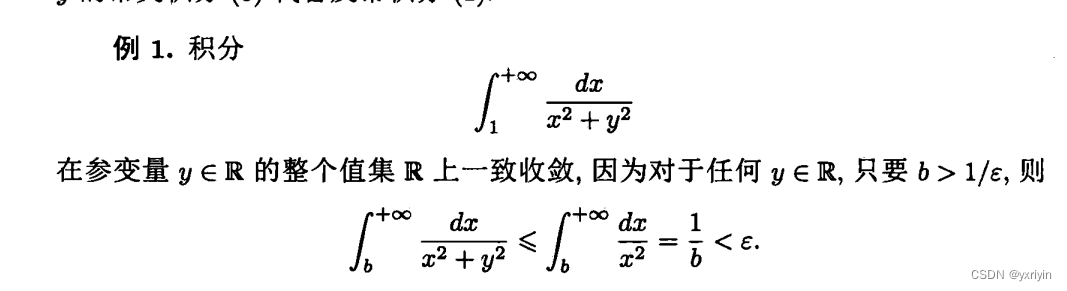 我们要证明在足够大的情况下,这个积分是很小的。
我们要证明在足够大的情况下,这个积分是很小的。



 各种可交换。一般我们认为大部分能列出来的都是可交换的。
各种可交换。一般我们认为大部分能列出来的都是可交换的。

反常积分的技巧真是千奇百怪。


还是各种可交换。

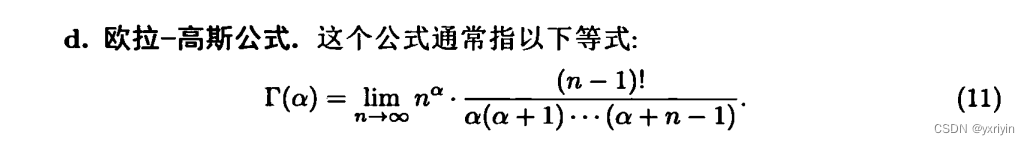




终于开始讲卷积了。物理中的卷积,是针对输入信号f,通过一个仪器的算子A,变成输出信号。如果A是一个平移变算子,也就是时间推移后,依然产生完全一样的信号,只是t不同。
 要根据输入信号来求输出信号。要根据输出信号反推输入信号。一般来说,只要知道仪器对脉冲的响应,就可以知道所有它对其他信号的响应。
要根据输入信号来求输出信号。要根据输出信号反推输入信号。一般来说,只要知道仪器对脉冲的响应,就可以知道所有它对其他信号的响应。

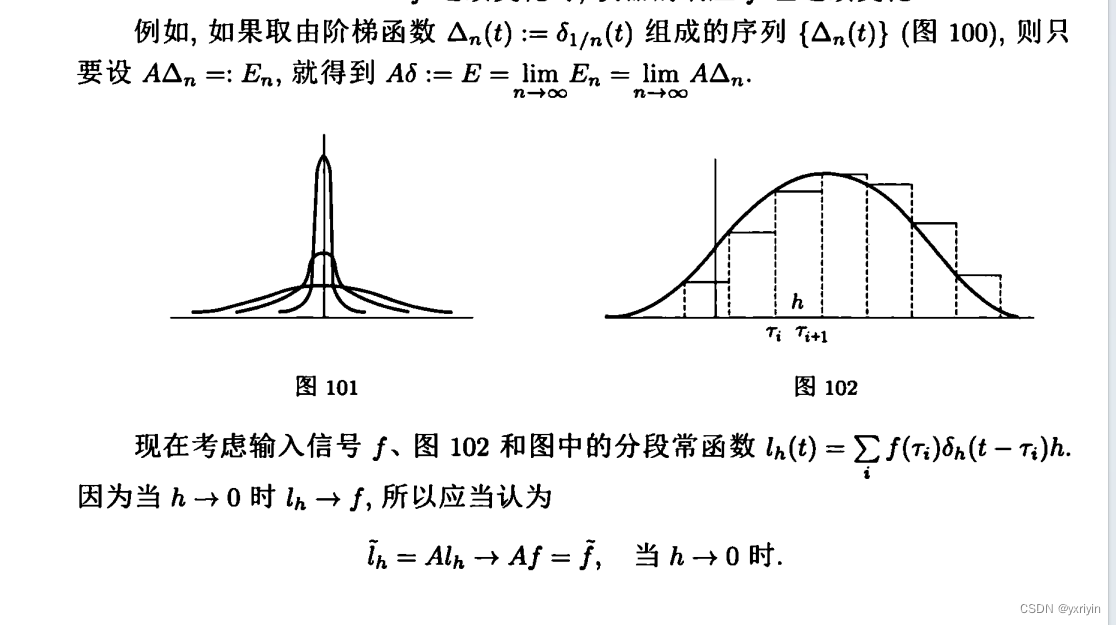
重点来了,我们一个普通的信号f,可以看成分段函数,而当分段趋于无穷的时候,分段函数就趋于f,而这个分段函数,可以用脉冲函数求和来表示。这个真是太秒了。原来是这么理解的。

因为算子是线性的,所以可以把A挪进去。最后我们得到了一个卷积的公式。所以我们第一个问题得到了解决,为什么知道脉冲函数的响应,就能知道所有其他函数的响应。通过卷积即可。而这个卷积很有意思,首先它引入了两个未知变量,其中一个是被积变量,而另一个是参变量。一般,我们可以认为,对于原始函数f(t),我们通过引入了一个脉冲函数,实际也引入了一个额外的时间平移变量。这个引入的时间平移变量,是最终会被积分的。而t本来就是原始函数的变量。

这样,我们就定义了一个更加一般的卷积。
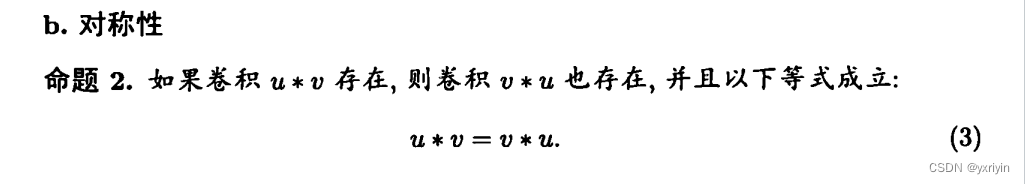

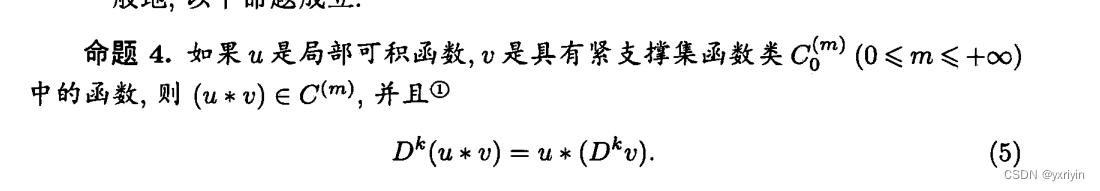
这些都是卷积的重要性质。
 这也是一个很重要的例子,我们一个函数和一个脉冲函数卷积,会取到一个平均的作用。
这也是一个很重要的例子,我们一个函数和一个脉冲函数卷积,会取到一个平均的作用。
显然,如果alpha趋向于0,那么自然这个积分就是f(y)了。因为积分就是面积,面积除以底,那自然就是高了。


 这个的意思是说,一些函数可能不是无限次可微的,那么我们把它和某个 特定的函数卷积后,就可以得到一个无限次可微的函数,而且他是逼近原始函数的。
这个的意思是说,一些函数可能不是无限次可微的,那么我们把它和某个 特定的函数卷积后,就可以得到一个无限次可微的函数,而且他是逼近原始函数的。

这个也很吊,可以用多项式逼近所有区间上的连续函数。
 这里要注意,我们用了卷积,自然就会引入一个新的被积变量,它应该是看成一个常数。
这里要注意,我们用了卷积,自然就会引入一个新的被积变量,它应该是看成一个常数。

所有周期函数都可以用cos sin来逼近。
后面含参变量的重积分也是各种可交换,就不提了。