PCA

协方差矩阵的特征向量是PCA主成分的方向。

数据----去中心化-------协方差矩阵---------特征向量表示坐标轴方向，特征值表示坐标轴方向的方差

缺点：受离群值的影响很大

主成分分析（Principal Component Analysis，PCA）是一种多变量统计方法，它是最常用的降维方法之一，通过正交变换将一组可能存在相关性的变量数据转换为一组线性不相关的变量，转换后的变量被称为主成分。

思考：我们如何得到这些包含最大差异性的主成分方向呢？

答案：事实上，通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值特征向量，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中，实现数据特征的降维。

由于得到协方差矩阵的特征值特征向量有两种方法：特征值分解协方差矩阵、奇异值分解协方差矩阵，所以PCA算法有两种实现方法：基于特征值分解协方差矩阵实现PCA算法、基于SVD分解协方差矩阵实现PCA算法。

降维的图像解释：

 

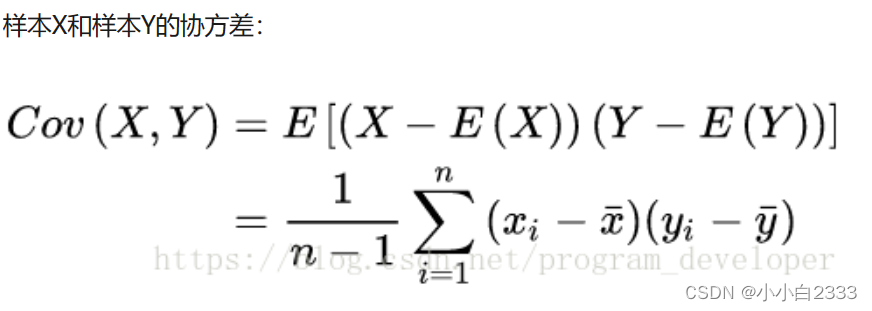
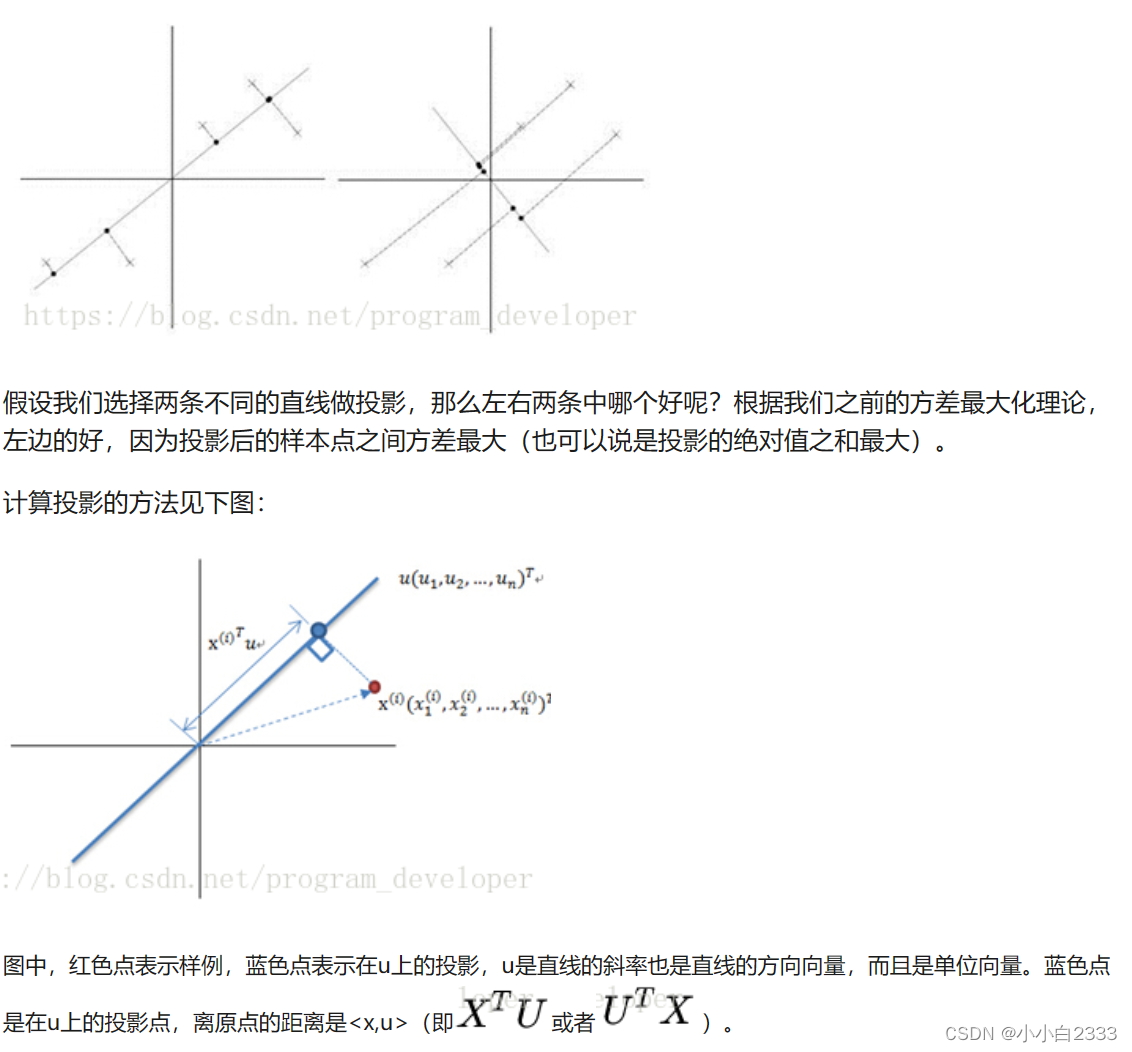
降维的公式解释

在数据中定义了两个轴，第一个轴的方向是第一个特征向量v1，第二个轴的方向是第二个特征向量v2。

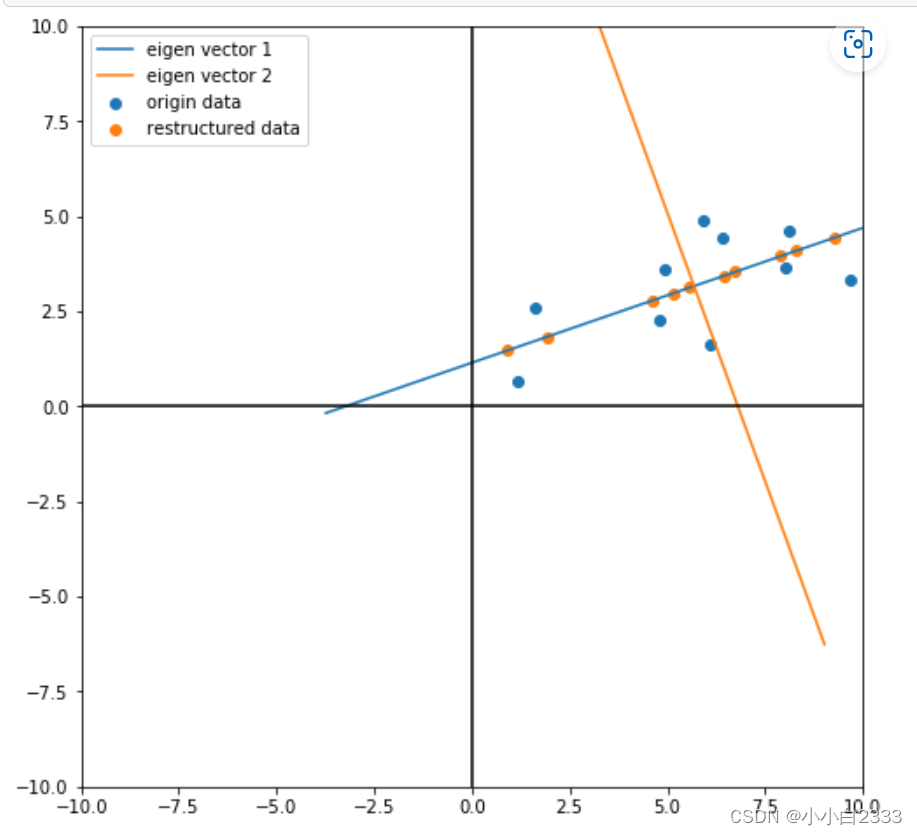
SVD（奇异值分解）

奇异值就是特征值的开平方。

SVD的V是PCA主成分的方向

用SVD主要是想用SVD求出主成分的方向向量

什么要用SVD来做PCA

很巧的是，SVD中的右奇异矩阵V，就是PCA的主成分

在PCA降维中，我们需要找到样本协方差矩阵C的最大k个特征向量，然后用这最大的k个特征向量组成的矩阵来做低维投影降维。
可以看出，在这个过程中需要先求出协方差矩阵,当样本数多、样本特征数也多的时候，这个计算量还是很大的。当我们用到SVD分解协方差矩阵的时候，SVD有两个好处：

        1.有一些SVD的实现算法可以先不求出协方差矩阵C也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解而是通过SVD来完成，这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是特征值分解。

        2.

部分参考：

https://blog.csdn.net/program_developer/article/details/80632779

12-.ipynb · ni1o1/pygeo-tutorial - Gitee.com

主成分分析（PCA）原理详解-CSDN博客