代码随想录Day18 LeetCode235 二叉搜索树的公共祖先 T701二叉搜索树中的插入操作 T140 删除二叉搜索树中的公共节点-编程知识

LeetCode T235 二叉搜索树的公共祖先

题目链接235. 二叉搜索树的最近公共祖先 - 力扣（LeetCode）

题目思路

此题不涉及遍历顺序.

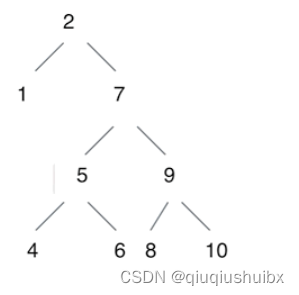
关于二叉搜索树的定义,这里我就不过多赘述了,前面几篇都说清楚了,根节点比左子树元素都大,比右子树元素都小,这道题我们就可以知道,两个节点的最近公共祖先一定满足夹在两个节点的中间这个条件.

那么,夹在两个节点之间的一定是最近的公共祖先吗?

答案是肯定的,我们不妨这样想,如果我们的节点这个时候再向左遍历,我们就会丢失右子树包含的那个节点,左子树同理.思路理顺了我们就来书写代码吧.

递归三部曲

1.函数参数和返回值
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) 
2.终止条件

如果遇到空节点,直接返回空节点即可
         if(root == null){return null;}
3.一次递归逻辑
         if(root.val>q.val && root.val>p.val){TreeNode left = lowestCommonAncestor(root.left,p,q);if(left != null){return left;}}if(root.val<q.val && root.val<p.val){TreeNode right = lowestCommonAncestor(root.right,p,q);if(right != null){return right;}}return root;
其实我么也发现了,无论遇不遇到空节点都可以直接返回,那么我们的代码又可以进一步的简化.

题目代码

class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root == null){return null;}if(root.val>q.val && root.val>p.val){TreeNode left = lowestCommonAncestor(root.left,p,q);if(left != null){return left;}}if(root.val<q.val && root.val<p.val){TreeNode right = lowestCommonAncestor(root.right,p,q);if(right != null){return right;}}return root;}
}//上述代码的简化版
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);return root;}
}//迭代法
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {while(true){if(root.val>q.val && root.val>p.val){root = root.left;}else if(root.val<q.val && root.val<p.val){root = root.right;}else{break;}}return root;}
}

LeetCode T701 二叉搜索树中的插入操作

题目链接701. 二叉搜索树中的插入操作 - 力扣（LeetCode）

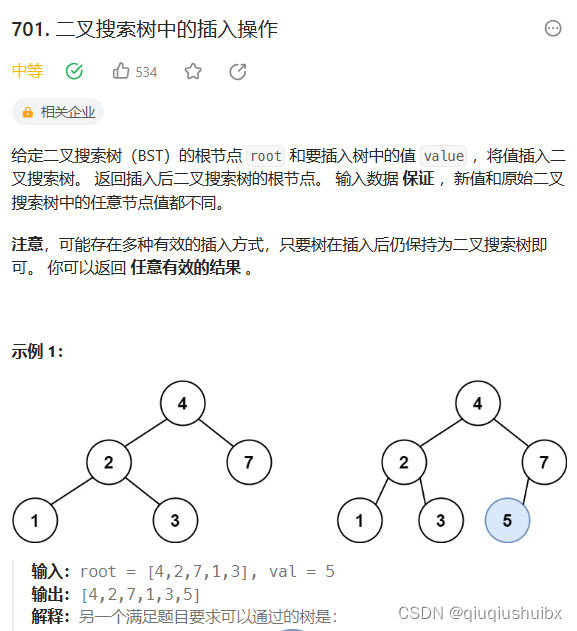
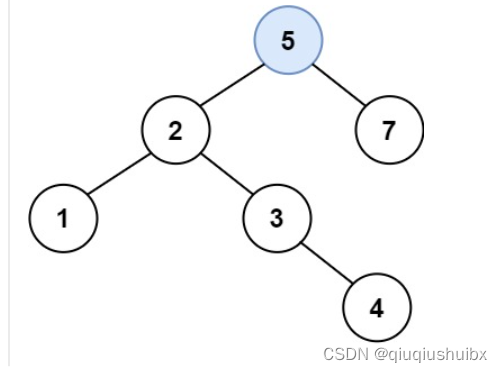
题目思路

这里我们看到这道题可以改变二叉搜索树的形状,可以返回任意有效的结果,我们就有点慌,其实这里我们所有节点的插入都可以在叶子节点完成,无论插入什么大小的节点我们都可以插入在叶子节点来解决问题.那么有了这个思路题目就变得简单了,我们只需要找到对应的叶子节点,创建一个新节点再连接即可.下面我们看看代码怎么写.

函数参数以及返回值

这里就用LeetCode本身提供的函数即可

2.终止条件

遇见空节点就说明我们找到了,直接创建新节点,向上返回即可
         if(root == null){TreeNode node = new TreeNode(val);return node;}
3.单次递归

如果在左边插入,就用左子树来接收这个节点,反之用右子树来接收
        if(val<root.val){root.left = insertIntoBST(root.left,val);}if(val>root.val){root.right = insertIntoBST(root.right,val);}return root;

题目代码

class Solution {public TreeNode insertIntoBST(TreeNode root, int val) {if(root == null){TreeNode node = new TreeNode(val);return node;}if(val<root.val){root.left = insertIntoBST(root.left,val);}if(val>root.val){root.right = insertIntoBST(root.right,val);}return root;}
}

LeetCode T140 删除二叉搜索树的节点

题目链接450. 删除二叉搜索树中的节点 - 力扣（LeetCode）

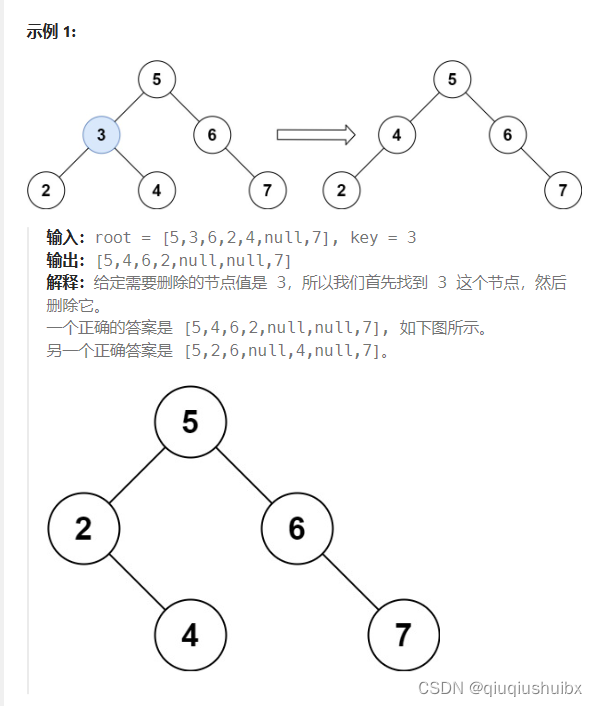
题目思路

这里我们先考虑五种可能的情况

1.找不到这个key对应的节点

2.能找到

2.1这个节点是叶子结点

直接返回空即可

2.2这个节点的左孩子为空,右孩子不为空

返回右孩子

2.3这个节点的左孩子不为空,右孩子为空

返回左孩子

2.4这个节点左右孩子都不为空

这个的处理较为复杂,我们举个例子说明

假设我们要删除7节点,我们就得调整二叉树的结构

假设我们保留右子树(保留左子树也可以,方法一样)

我们找到右子树中的最小值(右子树中的左子树的最小值),将原左子树接在这个节点下面即可

递归逻辑

1.确定递归函数以及返回值

使用函数本身即可

2.确定终止条件

由于这次的终止条件是找到节点的过程,所以较为复杂
        if(root == null){return null;}if(root.val == key){if(root.left == null && root.right == null){return  null;}else if(root.left != null && root.right == null){return root.left;}else if(root.right != null && root.left == null){return root.right;}else {TreeNode cur = root.right;while (cur.left != null) {cur = cur.left;}cur.left = root.left;root = root.right;return root;}}
3.确定一次递归逻辑
        if(root.val<key){root.right =  deleteNode(root.right,key);}if(key<root.val){root.left =  deleteNode(root.left,key);}return root;

题目代码

class Solution {public TreeNode deleteNode(TreeNode root, int key) {if(root == null){return null;}if(root.val == key){if(root.left == null && root.right == null){return  null;}else if(root.left != null && root.right == null){return root.left;}else if(root.right != null && root.left == null){return root.right;}else {TreeNode cur = root.right;while (cur.left != null) {cur = cur.left;}cur.left = root.left;root = root.right;return root;}}if(root.val<key){root.right =  deleteNode(root.right,key);}if(key<root.val){root.left =  deleteNode(root.left,key);}return root;}
}