本文展示了如何在 Python 中进行插值,并研究了不同的 2d 实现方法。 我们将讨论用于双变量插值的有用函数,例如 scipy.interpolate.interp2d、numpy.meshgrid 和 Python 中使用的用于平滑/插值 (RBF) 的径向基函数。
我们将使用 SciPy 和 Numpy 库实现插值,使其变得简单。
使用 scipy.interpolate.interp2d 在 Python 中创建二维插值
首先,让我们了解插值,这是一种在给定数据点之间构造数据点的技术。 假设有两个点,例如 1 和 2。
在此示例中,我们可以插值并找到点 1.22 和 1.44,等等。
机器学习中经常使用插值来填充数据集中缺失的数据,称为插补。 插值经常用于使数据集的点更均匀。
让我们看看使用 scipy.interpolate 模块在 Python 中处理插值示例。
interp2d 是 interp1d 函数的直接概括。 此函数将可用数据点的 x 和 y 坐标作为单独的一维数组,并将每对 x 和 y 坐标的值作为二维数组。
假定数据点位于规则且均匀的 x 和 y 坐标网格上。 一般函数形式如下。
class scipy.interpolate.interp2d(x, y, z, kind='linear', copy=True, bounds_error=False, fill_value=None)
其中 x、y 和 z 是数组,种类可以是 {'linear', 'cubic', 'quintic'} 或可以保留为可选。
#import libraries
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt# x,y arrays
x = np.arange(-5.01, 5.01, 0.25)
y = np.arange(-5.01, 5.01, 0.25)
xx, yy = np.meshgrid(x, y) #see details below for 'np.meshgrid'#approximate function which is z:= f(x,y)
z = np.sin(xx**2+yy**2)
fun = interpolate.interp2d(x, y, z, kind='linear') # kind could be {'linear', 'cubic', 'quintic'}
xnew = np.arange(-5.01, 5.01, 1e-2)
ynew = np.arange(-5.01, 5.01, 1e-2)
znew = fun(xnew, ynew)plt.plot(x, z[0, :], 'go-', xnew, znew[0, :], 'b-')
plt.show()
输出:
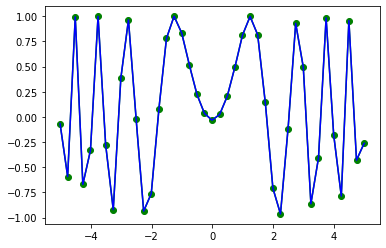
%> 请注意 ,我们使用了 numpy.meshgrid 来制作网格; 你可以用两个代表笛卡尔或矩阵索引的一维数组制作一个矩形网格。
一般函数形式如下。
numpy.meshgrid(*xi, copy=True, sparse=False, indexing='xy')
xi代表一维坐标数组x1,x2,…,xn。
使用 scipy.interpolate.Rbf 在 Python 中创建用于插值的径向基函数
此类插值用于n维散点数据的情况; 为此,我们使用 scipy.interpolate.Rbf。
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate.rbf import Rbf # radial basis functions# x y arrays
x = [1, 1, 2 ,3, 4, 4, 2, 6, 7]
y = [0, 2, 5, 6, 2, 4, 1, 5, 2]
z = [1]*len(x)#RBF Func
rbf_fun = Rbf(x, y, z, function='gaussian')x_new = np.linspace(0, 8, 81)
y_new = np.linspace(0, 8, 82)x_grid, y_grid = np.meshgrid(x_new, y_new)
z_new = rbf_fun(x_grid.ravel(), y_grid.ravel()).reshape(x_grid.shape)plt.pcolor(x_new, y_new, z_new);
plt.plot(x, y, 'o');
plt.xlabel('x'); plt.ylabel('y');
plt.title('RBF Gaussian interpolation');
输出:
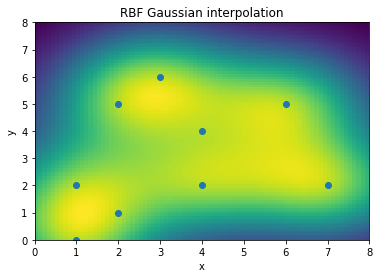
此类插值函数使用径向基函数 (RBF) 将 N-D 散点数据转换为 M-D。 可以使用 RBF 插值法对 n 维的散乱数据进行平滑和插值。
不过,由于存在外推的可能性,例如获取数据范围之外的值,因此应谨慎进行。