一、Lingo软件介绍

1、lingo软件的简单介绍

美国芝加哥大学的Linus Schrage教授于1980年左右开发的专门用于求解最优化问题的软件包，后经多年完善与扩充，并成立了LINDO系统公司进行商业运作取得巨大成功。根据 LINDO公司主页（http://www.lindo.com)提供的信息，位列《财富》杂志500强的企业中，有一半以上使用Lingo优化软件，前25强有23企业使用Lingo优化软件。用户可以在主页自由下载各类子包的演示版和应用例子。演示版和正式版功能类似，只是求解问题规模受到限制。各类版本的限制如下表

版本类型	总变量数	整数变量数	非线性变量数	约束数
演示版	300	30	30	150
求解包	500	50	50	250
高级版	2000	200	200	1000
超级版	8000	800	800	4000
工业版	32000	3200	3200	16000
扩展版	无限	无限	无限	无限

LINGO是英文Linear Interactive and General Optimizer首写字母的缩写，即“交互式线性和通用优化求解器”。

Lindo/Lingo软件内部有以下4个求解程序用于求解不同类型的优化模型

直接求解器(Direct Solver)
线性优化求解程序（Linear Solver)
非线性优化求解程序（Nonlinear Solver)
分支定界管理程序（Branch and Bound Manager)

对于已经输入的一个优化模型，一旦发出求解指令，第一步是对等式约束的直接处理，例如，如果约束中有三个等式约束

xyz=30,
x+y=8,
y=5

则Lingo软件能直接确定y=5,x=3,z=2，这三个变量就变成常数了。这样就尽量减少模型的规模(变量数和约束数）,从而使得求解更加有效快捷。第二步就是识别模型的类型，根据类型调用不同的处理器来求解。

而处理器识别模型会在计算界面给出说明：

LP：线性规划模型
QP：二次规划模型
NLP：非线性规划
ILP：整数线性规划
INLP：整数非线性规划
IQP：整数二次规划

2、使用lingo求解优化模型应该注意的几个问题

尽量使用实数优化模型，尽量减少整数约束和整数变量的个数；
尽量使用光滑优化模型，尽量避免使用非光滑函数；（尽量少用绝对值函数(|x|)、符号函数（当x<0,函数为-1，x=0时，函数为0，当x>0时，函数为1）、多个变量求最大（或最小）、四舍五入函数、取整函数等。）
尽量使用线性优化模型，尽量减少非线性约束和非线性变量（非线性约束中的变量）的个数；
合理设定变量的上下界，避免计算陷入“大海捞针”。
模型中使用的单位的数量级要适当（ Lingo计算时，最大数尽量不要超过最小数的1000倍，如果出现100000000与0.1的计算，误差很大！小数湮没于大数！）

举个例子，如果进行100000000（一亿）与0.1的计算，由于这两个数字之间相差很大，计算结果有可能出现较大的误差。这是因为计算机在表示数字时使用的是有限的二进制表示，如果一个数字过大，它的小数部分可能会被舍入或截断，导致计算结果不准确。在这种情况下，0.1这个较小的数可能会被表示成一个近似值，而且由于与较大数进行计算，计算结果可能会受到舍入误差的影响，进一步增大误差。

二、编写简单的优化程序

1、编写一个简单的LINGO程序

在lingo的编辑窗口输入如下规划（二次规划）

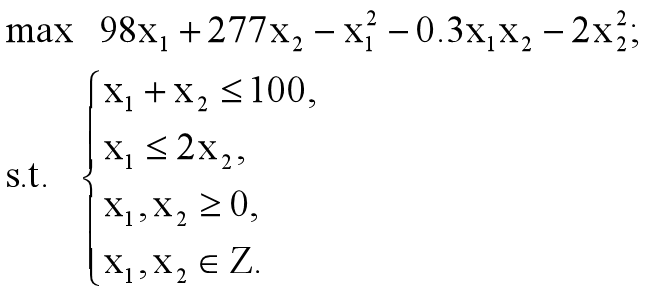
x1+x2<100;
x1<2*x2;
max=98*x1+277*x2-x1^2-0.3*x1*x2-2*x2^2;
@gin(x1);@gin(x2);！x1,x2取整;

注意：输入程序时，输入法状态是英文!!

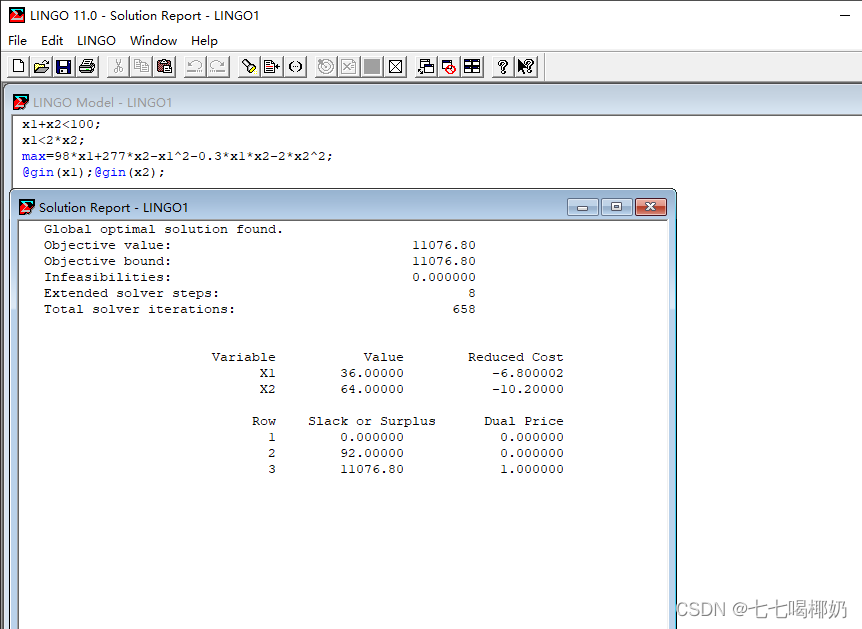
这段文字描述了一个优化问题的求解结果。下面对其中的各个内容进行解释：

- Global optimal solution found: 求解器找到了全局最优解，即在给定的约束条件下，找到了使目标函数取得最大（或最小）值的变量取值。

- Objective value: 目标函数的值，即在最优解下，目标函数所取得的数值。在这个问题中，目标函数的值为11076.80。

- Objective bound: 目标函数的边界值，即目标函数的最优解的理论上限（或下限）。与目标函数值相同，也为11076.80，表示找到的最优解是达到了目标函数的最优值。

- Infeasibilities: 不可行性的量度，即指约束条件是否满足。在这个结果中，所有约束条件均满足，不可行性为0.000000，表示所有约束都被满足。

- Extended solver steps: 求解器执行的扩展步骤数，表示在求解过程中，求解器进行了8次扩展步骤。

- Total solver iterations: 总的求解器迭代次数，表示在求解过程中，求解器进行了658次迭代。

- Variables: 相关变量的信息，包括变量名称、变量取值以及变量的减少成本（Reduced Cost）。在这个结果中，有两个变量X1和X2，它们的取值分别为36.00000和64.00000，并且对应的减少成本为-6.800002和-10.20000。

- Rows: 相关约束行的信息，包括行名称、松弛量或盈余量（Slack or Surplus）以及对应的对偶价格（Dual Price）。在这个结果中，有三个约束行，分别是行1、行2、行3。行1和行3的松弛量均为0.000000，表示约束条件被精确地满足。行2的松弛量为92.00000，表示约束条件有一定的余量。行3的对偶价格为1.000000，表示在最优解下，对应的约束条件对目标函数值的影响程度。

这些结果提供了关于优化问题求解的详细信息，包括最优解、约束条件情况以及相关变量和约束行的数值和性质。

2、lingo程序输入时的规范格式

Lingo总是根据“max=”或“min=”语句寻找目标函数，其它语句都是约束条件（注释句除外），即输入时不需要按顺序输入；
Lingo中不区分大小写字母，Lingo中的变量名可以超过8个字符，但不能超过32个字符，且必须以字母开头，其中不能含有中文；
Lingo中已假设所有变量都是非负的，所以当x>=0时，不必在输入计算机中，相反，如果有变量x可以取负数，则应规范@free(x)；（例如：y=sinx-1，数学上y取值于【-2,0】，如果是写在lingo程序中，就导致y==0!）
Lingo中的>=,<=可以用>,<替换，即不区分大于等于和大于，小于等于和小于；
输入的多余的空格和回车都会被忽略，一个约束可以分两行或者多行书写；
Lingo模型是由一系列语句构成，即语句是组成Lingo模型的基本单位，每个语句都是以分号“;”结尾，但尽量一个语句用一行来书写；
以感叹号“！”开始的语句是说明语句（注释语句，以便读者更好理解程序），但计算机在读取模型时，会忽略这样的语句。
在Lingo中，以“@”开头的都是调用函数（数据库），这在后面专门叙述。

3、程序计算（模型计算）的运行

4、Lingo程序常见错误

表示倍数的乘号“*”漏掉；
语句结束后漏掉分号“；”
变量名没有定义（数组sets中没有出现）；
函数标示“@”漏掉；
括号不配对；
sets,data后的冒号“：”漏掉，或 endsets,enddata(不是enddate!)多后加分号。
中文输入法忘记关闭！！

5、求解器状态的解读

启动lingo计算摁扭后，会弹出如下界面：

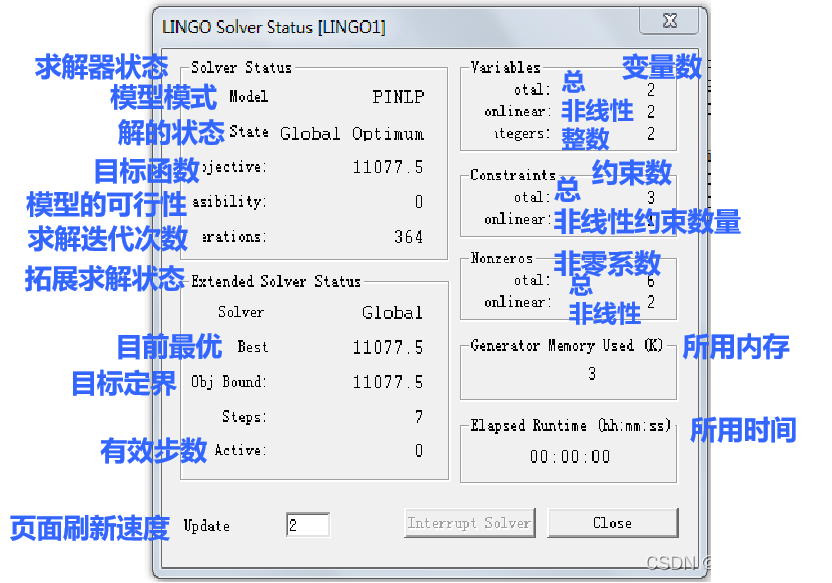
6、lingo求解状态窗口的注释

三、Lingo运算符与函数

1、算术运算符

+ - * / ^

加减乘除幂

算术运算符是数与数之间的运算，结果也是数。

2、逻辑运算符

2.1 逻辑值之间的运算符

#and# #or# #not#

与或非

2.2 逻辑表达式的比较符(不区分大小写)

#eq# #ne# #gt# #ge# #lt# #le#

等于不等于大于大于等于小于小于等于

这6个操作符实际还是“数与数之间的”比较，而逻辑表达式计算的结果是逻辑值。

例如表述为计算机能接受的逻辑表达： i#gt#3#and#i#le#7

参与运算的是逻辑值，结果也是逻辑值，逻辑值只有“真”（True=1)和“假”（False=0)两个值。

3、关系运算符

< (<=) >(>=) =

小于（小于等于）大于（大于等于）等于

这三个符号表示数与数之间的大小关系

4、lingo基本函数

4.1 基本函数

@abs(x)：   绝对值函数，返回x的绝对值；
@cos(x)：   x的余弦值，x是弧度值；  @acos(x)
@sin(x)：   x的正弦值，x是弧度值；  @asin(x)
@tan(x)：   x的正切值，x是弧度值；  @atan(x)
@exp(x)：   e^x；  
@log(x)：   ln(x);
@lgm(x)： 返回x的伽玛函数的自然对数，x为整数时，@lgm(x)=ln[(x-1)!]，x不是整数采用线性插值，即：  @lgm(4.3)≈0.7@lgm(4)+0.3@lgm(3)（是近似）
@mod(x,y)：   模函数，即x除以y的余数，x,y是整数；
@pow(x,y)：   x^y；
@sign(x)：     返回x的符号值,x>0,sign(x)=1；x<0,sign(x)=-1；x=0,sign(x)=0;
@floor(x)：     取整（返回x的整数部分）；
@sqr(x)：        x*x；
@sqrt(x)：       x的平方根；
@smin(list)：  返回数列list的最小值；
@smax(list)： 返回数列list的最大值；
@prod(list)：   返回连乘的积；