零、吴恩达专项课程引入

概念导入：边缘检测

假如有一张如下的图像，想让计算机搞清楚图像上有什么物体，有两种方法：检测图像的 垂直边缘 和 水平边缘。

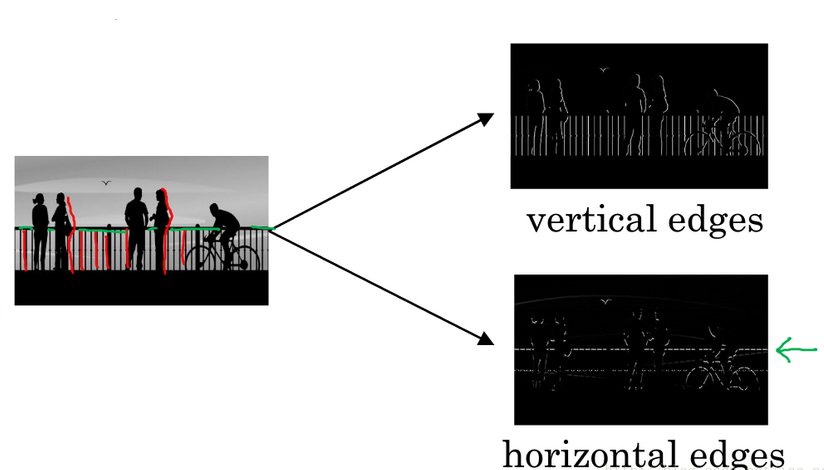
如下图所示，一个 6 * 6 的灰度图像，构造一个 3 * 3 的矩阵（ 在CNN中通常称为 filter 过滤器），将 3 * 3 矩阵映射到该图像中，对这个 6 * 6 的灰度图像做 卷积运算，filter 跟图片对应位置的数值直接相乘，所有的都乘完以后再相加（内积），其中步长为1，以此类推，让过滤器在图像上逐步滑动，对整个图像进行卷积计算得到一幅 4 * 4 的图像。

这种方法可以得到图像的边缘信息的主要解释如下：

下图 0 表示图像深色区域，10为图像亮色区域，同样用一个 3 * 3 过滤器（其中，1代表亮色、0代表灰色、-1代表更深的深色），对图像进行卷积计算，得到右侧的矩阵，代表的图像信息为中间亮，两边暗（30为亮色，0为暗色），有明显深浅交叉对比，其中 亮色区域 就对应图像边缘。

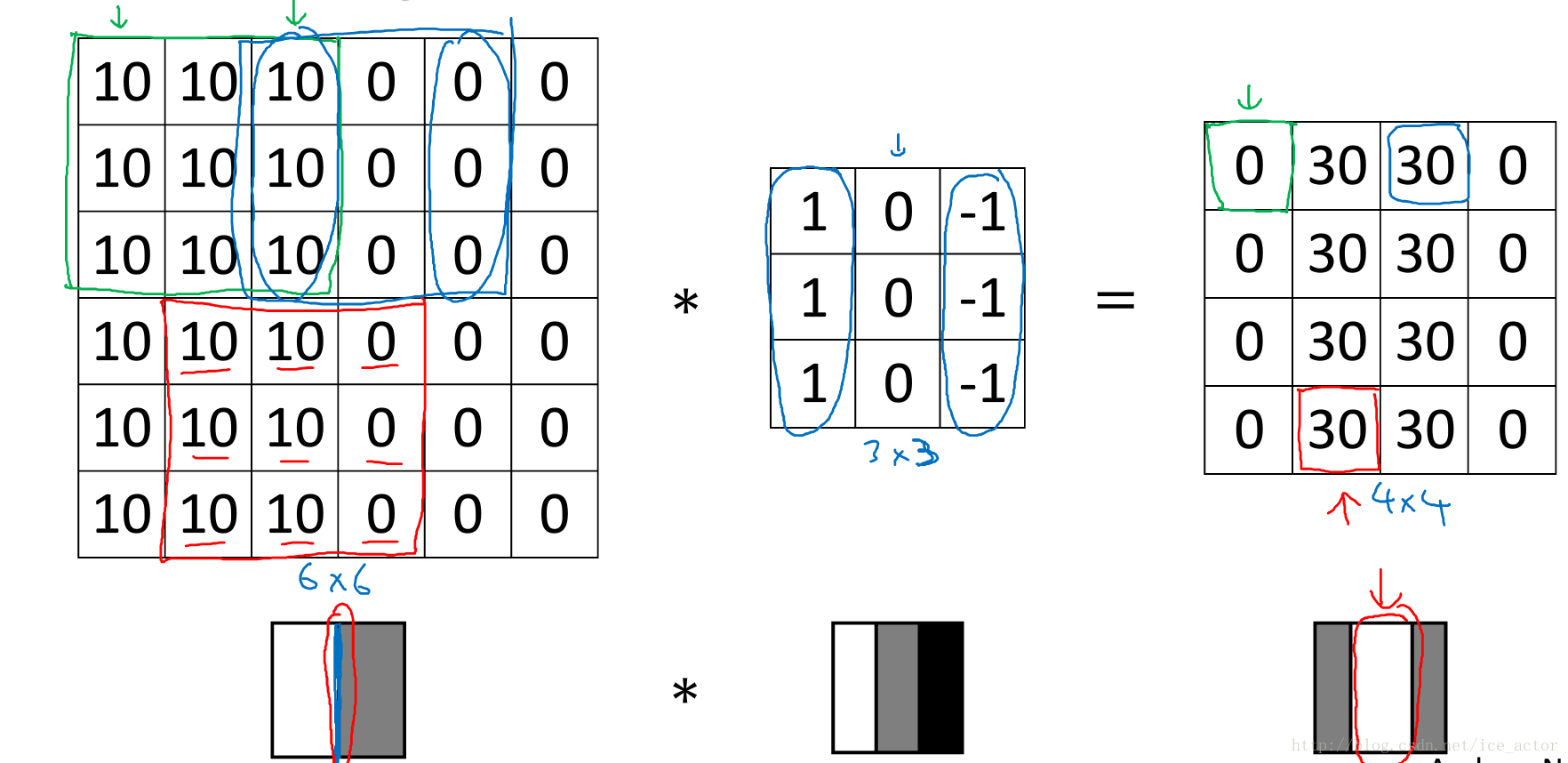
 通过水平过滤器和垂直过滤器，可以实现图像水平和垂直边缘检测。还有其他类型的滤波器，在处理其他适合的任务目标方面有很好的效果。

 总结

在卷积神经网络中我们要学习的便是这些滤波器 filter 的参数（神经元的权值 weight ），卷积神经网络训练的目标就是去理解过滤器的参数。

一、CNN 用于图像分类

基本步骤

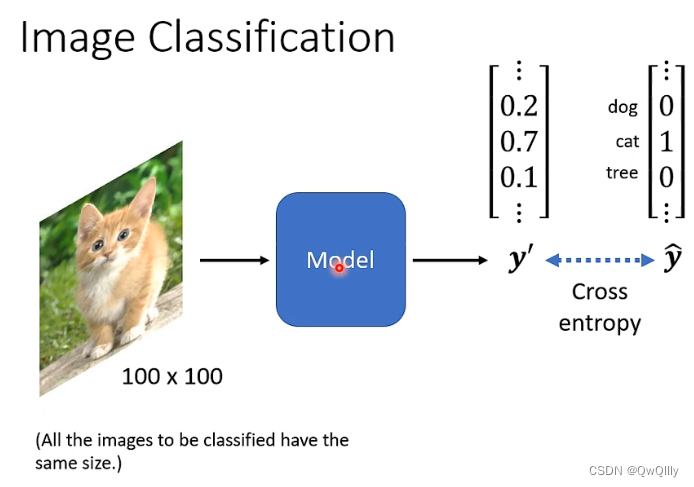
1. 把所有图片都先 Rescale 成大小一样
2. 把每一个类别,表示成一个 One-Hot 的 Vector（Dimension 的长度就决定了模型可以辨识出多少不同种类的东西,）
3. 将图像【输入】到模型中

如何将图片输入到模型中？⇒ 一般思路：展平→参数量过大

 彩色图像分为R G B 三层，展平后首尾相接

值代表着颜色的强度

 图像识别中不需要全连接的，参数太多了

基础卷积操作的缺点

参数过多，影响训练

如果输入图像的维度是 100 × 100 × 3，并且有 1000 个 Neuron，那第一层的 Weight 就有 1000 ×100 × 100 × 3（ 3×10 的 7 次方），是一个非常巨大的参数数量。

虽然随著参数的增加,我们可以增加模型的弹性,我们可以增加它的能力,但是我们也增加了 Overfitting 的风险。

解法1：设定 “感受野”（Receptive Field）

原理：Neuron 也许根本就不需要把整张图片当作输入，它们只需要把图片的一小部分当作输入，就足以让它们检测某些特别关键的 Pattern 有没有出现。例如：在检测鸟嘴的任务中，仅需要获取下图的鸟嘴周围红框部分的图像信息即可检测出鸟嘴

观测1：通过判断多个小局部图像就能判断出图片标签

 若要设置 “感受野”，每个神经元只需要考察特定范围内的图像信息，将图像内容展平后输入到神经元中即可。

简化1特点

• 感受野之间可以重叠
• 一个感受野可以被多个神经元选择（共享权重）
• 在设置感受野大小时，感受野可以“有大有小”（一般不做过大的kernal Size，常常设定为3*3）
• 感受野可以只考虑某一些 Channel
• 感受野可以是 “长方形” 的
• 感受野不一定要 “相连”

感受野的一般设定

每一个感受域有多个神经元守备。kernel size 是宽高大小，stride 是移动的步长，padding 是边界区域扩充补值（一般是补 0）。在移动时，我们希望感受域彼此之间有重叠，防止有 pattern 在边缘交界处检测不到。图片中的每个地方都要有感受域，从头开始一步步滑动直到整个图像区域扫描完成

1. 看所有的Channel

   一般在做影像辨识的时候会看全部的 Channel。那么，在描述一个 Receptive Field 的时候,无需说明其Channel数，只要讲它的高、宽⇒Kernel Size

   一般不做过大的kernal Size，常常设定为3 × 3

2. 每个感受野会有不止一个神经元进行“守备”⇒输出通道数/卷积核数目

3. 不同的感受野之间的关系⇒感受野的平移位移：stride【hyperparameter】

   一般希望感受野之间有重叠，避免交界处的pattern被忽略

4. 感受野超出影响的范围⇒padding（补值）

   补0；补平均值；补边缘值……

5. 垂直方向移动。

解法2：Parameter Sharing 权值共享（不同 Receptive Field 的 Neuron 共享参数）

原理：同样的 pattern，可能出现在图片的“不同位置”，不同感受域的神经元起同一个作用，侦测同样pattern的神经元做的工作是类似的 ⇒ 共享参数

例如下图所示，在检测鸟嘴的任务中，相当于一个滤波器扫描整张图片看有没有鸟嘴。

观测2：相同部分出现在不同区域

例如下图所示，虽然二者选择的 Receptive Field（感受野区域） 不一样，但是它们的参数一模一样。共享的其实就是参数 w，单个神经元的参数 w 是固定的，不会因为感受域不同而改变（当然 w 初始状态为未知，是需要学出来的）。所以同一个神经元针对不同的输入会有不同的输出

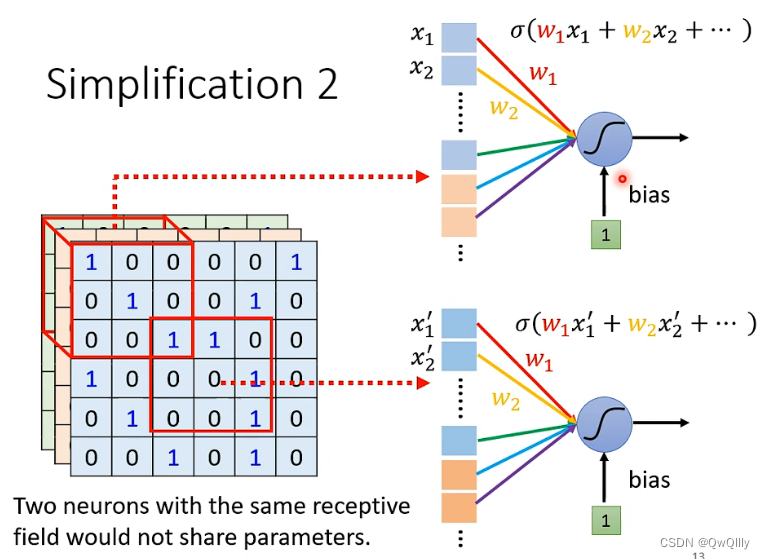
参数共享的一般设定

对每个感受野，都使用一组相同的神经元进行守备；这一组神经元被称作 filter（实质是同一套权重），对不同感受野使用的 filter 参数相同。

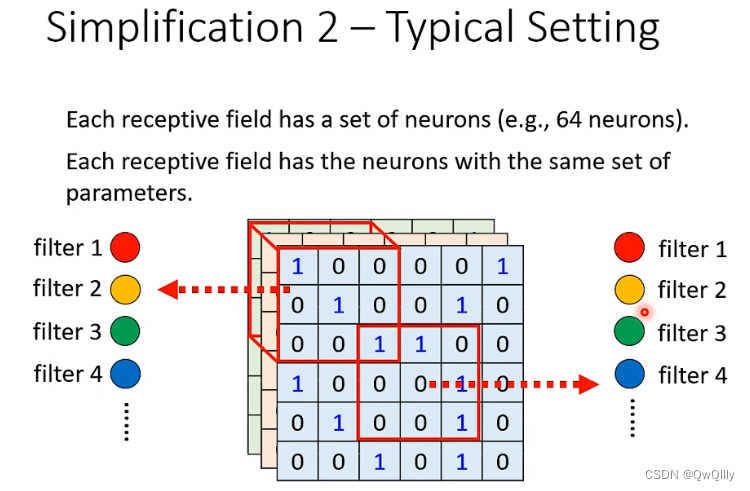
卷积的优势

卷积层是“受限”（弹性变小）的FC：

• FC可以通过“学习”决定要看到的“图片”的范围。加上“感受野”概念后，就只能看某一个范围。
• FC可以自由决定守备不同“感受野”的各个神经元参数。加上“权值共享”概念后，守备不同感受野的同一个滤波器（filter）参数相同。

分析：

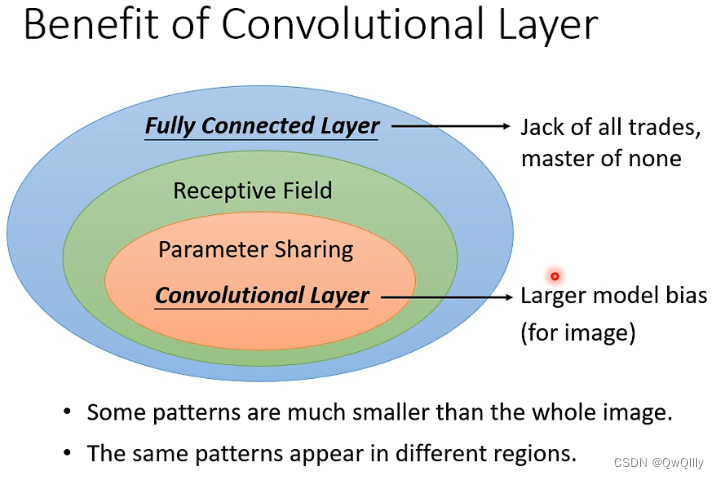
• 一般而言，Model Bias 小，Model 的 Flexibility 很高的时候，比较容易 Overfitting，Fully Connected Layer可以做各式各样的事情，它可以有各式各样的变化，但是它可能没有办法在任何特定的任务上做好
• CNN 的 Bias 比较大，它是专门為影像设计的，所以它在影像上仍然可以做得好。

二、另一角度切入

1.卷积层

卷积层中有若干个 filter，每个 filter 可以用来 “抓取” 图片中的某一种特征（特征 pattern 的大小，小于感受野大小）。filter 的参数即是神经元中的“权值（weight）”。

不同的  filter 逐步滑动扫描计算完成一张图的矩阵后，将会产生“新的图片”，其中 每个  filter  将会产生图片中的一个  channel  ⇒  这个结果即为 feature map（特征图）

filter的计算是“内积”：filter跟图片对应位置的数值直接相乘，所有的都乘完以后再相加。

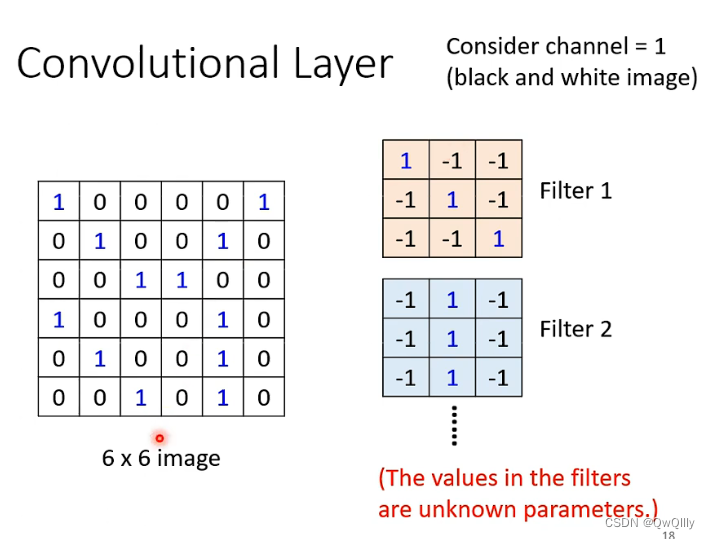
例如下图中的例子，选择的 3 * 3 滤波器对正对角线的信息敏感，因此利用此滤波器对左图矩阵的左上角进行卷积计算后，得到的结果为 3

多层卷积

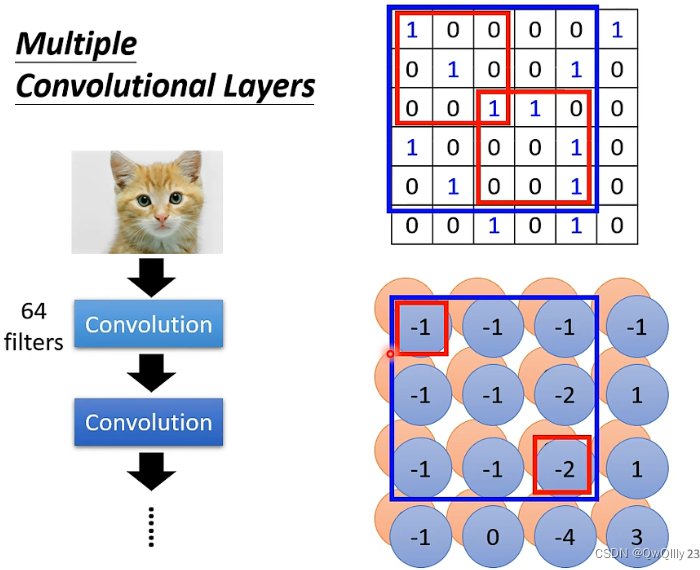
第一层的卷积结果，产生了一张3×3的feature map。继续卷积时，需要对64个channel都进行处理⇒filter的“高度”为64。

多层卷积⇒让“小”卷积核看到“大”pattern

在第二次卷积时，输入的原始图片信息增加了！

所以不是一直分区域处理的。随着层数的增加，考虑的范围会逐渐变大

这里，在第二层中考虑3×3的范围，在原图实际上考虑了5×5范围内的pattern。当卷积层越来越深时，即使只是3×3的filter，看到的范围也会越来越大。

卷积运算中也有Bias，描述时一般“忽略”

2.padding 和 卷积步长 （stride）

上述卷积运算过程的缺点是：

① 卷积操作会降低卷积图像的大小，可能会使图像大小越来越低

② 图像的边角元素只被一个滤波器进行计算并输出使用，因此这些图像边缘的像素在输出中采用较少，也意味着丢掉了很多图像边缘的信息

解决方法：

① 引入了 padding 操作（习惯上用0来填充），也就是在图像卷积操作之前，沿着图像边缘用0进行图像填充。对于3*3的过滤器，我们填充宽度为1时，就可以保证输出图像和输入图像一样大。

② 引入 卷积步长 stride （过滤器在图像上滑动的距离）

加入 padding 和 stride 后卷积图像大小的通用计算公式为：

3. 补充知识点

①  参数大小： 例如有 10 个  3 * 3 的过滤器，每个过滤器都有 3 * 3 * 3 + 1 = 28 个参数（其中，3 * 3 * 3 为过滤器大小，1 是偏差系数）

②  每经过一组 过滤器的计算后 ，输出图像的通道数 就是 过滤器的个数

③  1 x 1 卷积可以在保证高度宽度不变的情况下压缩信道数量并减少计算（降维）。

④ 迁移学习：冻结前面所有的层，只把softmax层改动以适应自己的实现。

三、两种介绍的对比

分享的权重其实就是filter

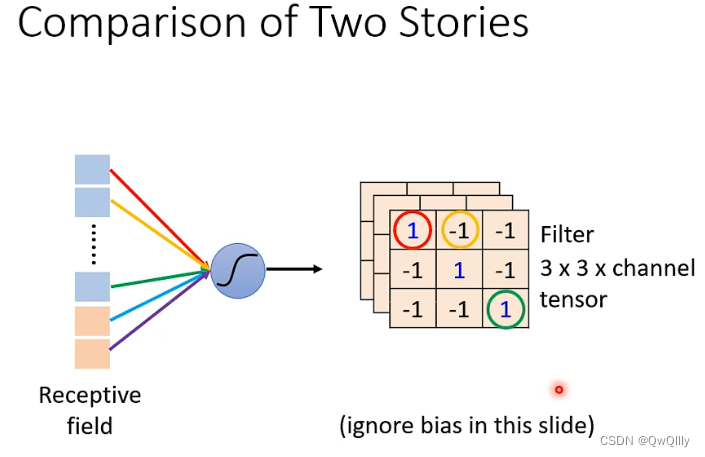
 卷积 = 不同的filter扫过整个矩阵 = 不同的感受野公用权重参数

不用看整张图片范围：

• 神经元角度：只要守备感受野
• 滤波器角度：使用滤波器侦测模式pattern

图片不同位置的相同模式pattern：

• 神经元角度：守备不同感受野的神经元共用参数
• 滤波器角度：滤波器“扫过”整张图片

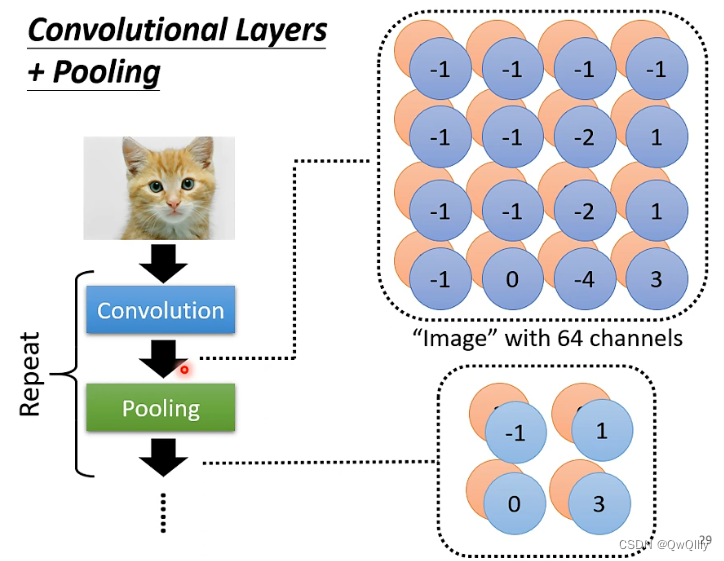
解法3：Pooling（池化）把图片变小，减小运算量

观测3：截出主要元素不会改变标签

引入池化层，池化的目的就是挑出重要的信息，然后缩小规模，减小运算量，提升运算速度。但是会造成精确度下降。

Pooling本身没有参数,所以它不是一个 Layer，没有要 Learn 的东西。行为类似于一个 Activation Function,（Sigmoid ， ReLU ），是一个 Operator，它的行為都是固定好的。

分类：

• Max pooling
• Avg Pooling
• ……

大小：可以调整

例如下图通过滤波器产生了4x4 的数字图，按照方框分成四组，每一组中选最大值做为该组代表，这就叫 max pooling（最大池化）。

假如是将每一组的平均值作为该组代表，那么就叫做 mean pooling （平均池化）。

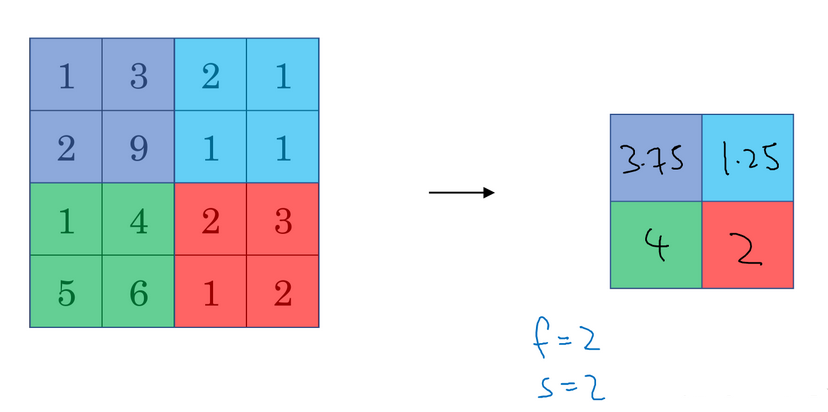
 平均池化和最大池化唯一的不同是，它计算的是区域内的平均值而最大池化计算的是最大值。在日常应用使用最多的还是最大池化，除了一些较深的神经网络。

池化的超参数：步长 stride 、过滤器大小 filter size 、池化类型最大池化 / 平均池化

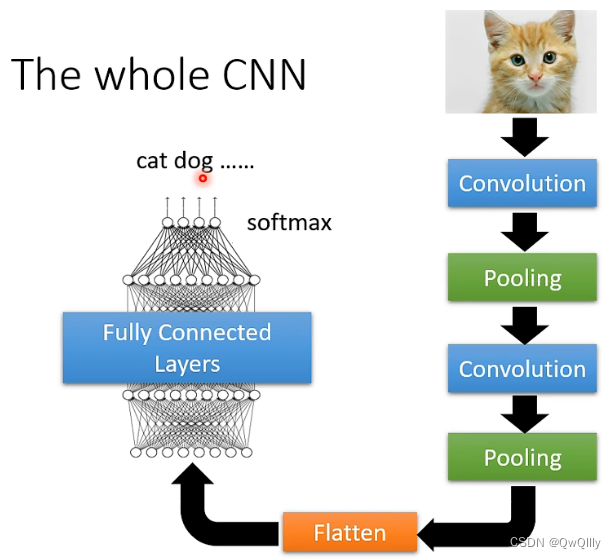
四、CNN全过程总结

一般：卷积与池化交替使用。pooling⇒可有可无（算力支撑）

Pooling对於 Performance,会带来一点伤害的。如果你运算资源足够支撑你不做 Pooling 的话,很多 Network 的架构的设计,往往今天就不做 Pooling,全 Convolution。

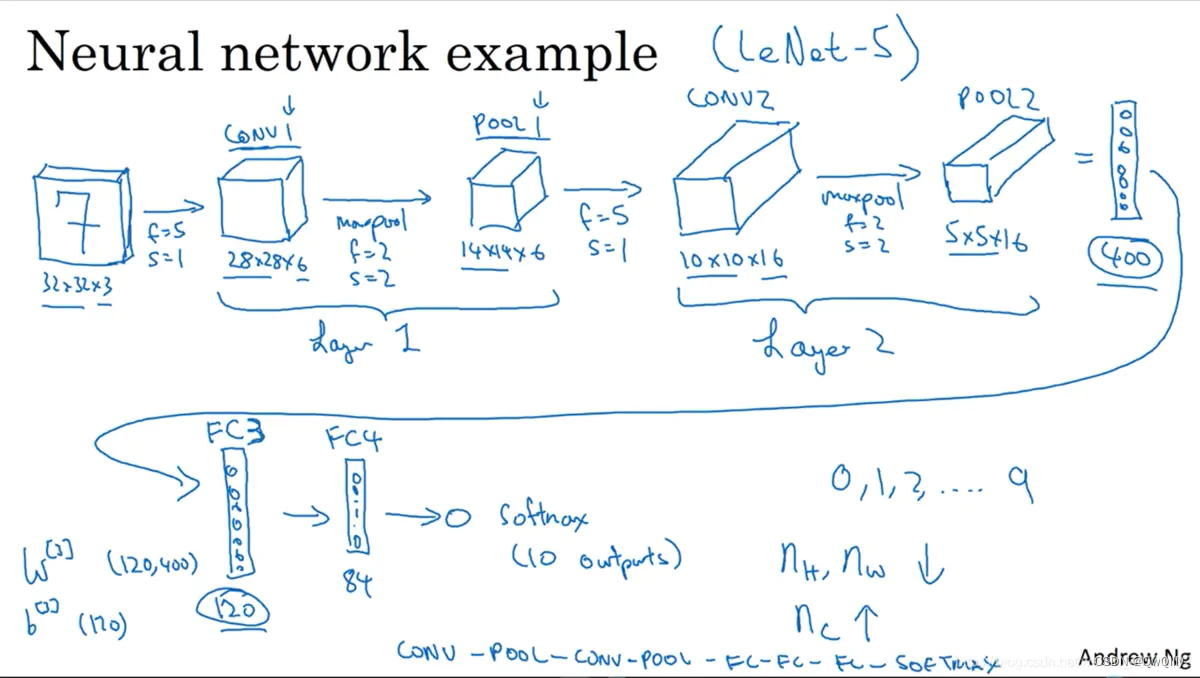
通过卷积层，池化层，拉直（flatten），全连接层，softmax 后，输出结果去分类。不过随着技术的提高，运算能力越来越强，可以不使用池化层来提高精确度（因为现在很多实验环境算力都够用，池化层的目的显得越来越没必要，所以在设计每一模块的时候都要考虑当前任务及实验环境，根据这些因素去设计最符合的网络）。

五、应用：Alpha Go

把棋盘看成19×19的图片，用48个channel来描述，代表48个状态

下围棋与“图像辨识”的共同点

• 只看小范围
• 模式在不同位置出现。

不同点：没有Pooling

由于棋子不能省略，用于围棋中不能加入池化层

更多应用：语音、自然语音处理。。。

To Learn More：CNN的缺陷——空间变换

⇒data augmentation/spacial transformer（下一讲）

CNN 并不能够处理影像放大缩小,或者是旋转的问题。所以在做影像辨识的时候,往往都要做 Data Augmentation，把你的训练数据截一小块出来放大缩小、把图片旋转，CNN 才会做到好的结果。

有一个架构叫 spacial Transformer Layer可以处理。