[Open In Colab]

import numpy as np
import matplotlib.pyplot as plt

1. 线性回归简介

简单的线性回归就是使用一根直线去拟合一种趋势。

例如：我们有一批房屋面积与房价的数据。将其作成散点图如下：

X = [100, 110, 120, 130, 140]  # 房屋面积（m^2）
y = [100 * 1, 110 * 1.05, 120 * 1.1, 130 * 0.95, 140 * 0.9]  # 房价（万元）plt.scatter(X, y, c='red')
plt.ylim(80, 160)
plt.xlim(80, 160)
plt.show()

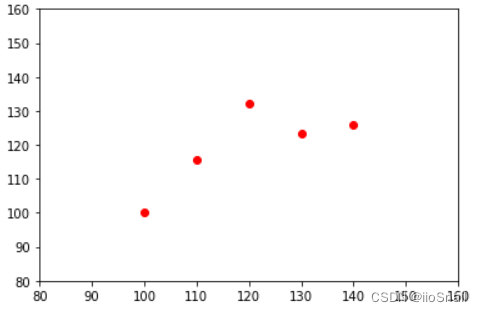
此时，我们通过观察图像，可以假设房屋面积与房价是呈一种线性关系的。也就是：$房价=a\ast 房屋面积+b$ 。但我们并不知道 $a$ 和 $b$ 的值。

线性回归的目标就是求出这条直线，也就是 $a$, $b$ 的值。

通过我上面的数据可以很容易看出，它们的线性关系为：$房价=1\ast 房价+0$。即 $a=1,b=0$

plt.ylim(80, 160)
plt.xlim(80, 160)
plt.scatter(X, y, c='red')
plt.plot(np.arange(80, 160), np.arange(80, 160) * 1 + 0, c='green')
plt.show()

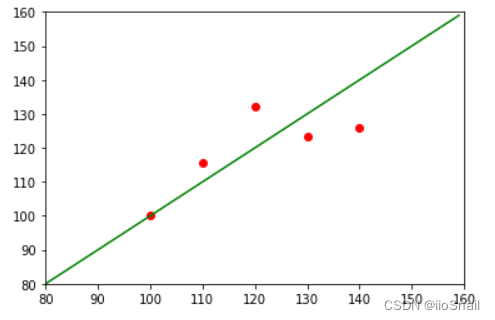
接下来，需要使用sklearn去实现这条直线的计算。

2. 使用sklearn进行一元线性回归

sklearn进行线性回归使用的是sklearn.linear_model，只需要给出上面的X和y即可自动进行数据拟合。

首先定义模型：

from sklearn import linear_modelmodel = linear_model.LinearRegression()

之后构造数据集：

需要有X和Y，其中X的维度必须是(样本数, 特征数)。
在该例子中，我们有5条数据，一个面积的特征。因此需要将X的维度处理成(5, 1)
而Y因为是一个具体的值，因此其维度必须是(样本数,)

在上面定义X，y时，y已经满足了维度。而X维度为(样本数, )，因此需要对其进行转换。

X = np.array(X).reshape(-1, 1)  # -1表示自动计算维度，因此效果等同于`.reshape(5, 1)`
model.fit(X, y)  # 训练模型

LinearRegression()

模型训练后，即可使用predict方法进行预测：

print(model.predict(X))

[107.4 113.4 119.4 125.4 131.4]

现在我们将训练好的进行绘制

X_ = np.arange(80, 160).reshape(-1, 1)
y_ = model.predict(X_)plt.scatter(X, y, c='red')
plt.plot(X_, y_, c='blue')
plt.show()

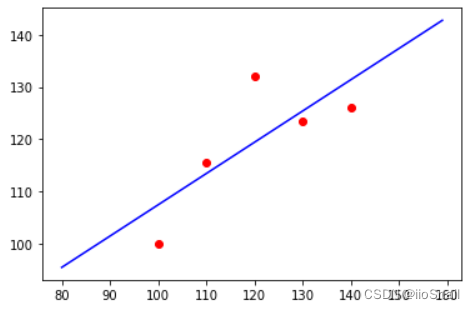
可以看到，我们训练出的模型和预测的模型还是有一定的差距的。这是因为我们的样本太少，导致无法拟合出真实的模型。

3. 线性回归的coef_参数和intercept_参数

上面我们训练好了模型。如果我们想要用数学表达式的方式写出来，可以通过查看模型的coef_和intercept_参数。

上面我们说过，X的特征只有一个。因此我们的线性回归模型的基础假设就是 y=f(x)=ax+b。因此，线性回归过程就是求a,b两个值。

我们可以通过coef_参数查看a的值，通过intercept_查看b的值

a = model.coef_[0]
b = model.intercept_
print("a =", model.coef_)
print("b =", model.intercept_)

a = [0.6]
b = 47.39999999999998

上面可以看到model.coef_返回的是一个数组，这是因为实际应用中，我们不止有一个特征，因此是一个数组。

下面我们尝试使用公式的方式去计算y，并进行绘制。

X_ = np.arange(80, 160).reshape(-1, 1)
y_ = a * X_ + bplt.scatter(X, y, c='red')
plt.plot(X_, y_, c='blue')
plt.show()

可以看到，我们使用ax+b的计算方式得到了同样的结果。

4. 使用sklearn实现多元线性回归

在实际应用中，并不是所有的数据都是线性关系。数据可能会呈现出二次或三次曲线。例如，我们先构造出一个符合三次曲线的样本

X = np.sort(np.random.uniform(-3, 3, size=100))  # 定义100个X
y_true = -0.5 * (X ** 3) + 0.8 * (X ** 2) + 1 * (X ** 1) + 10  # 真实的y值
y_label = y_true + np.random.normal(-1, 1, size=100)  # y的标签值，含噪音plt.scatter(X, y_label, c='red')
plt.plot(X, y_true, c='green')
plt.show()

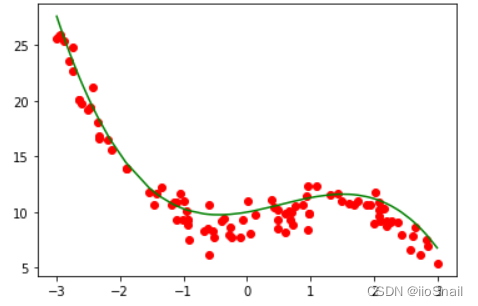
对于该样本，我们需要假设样本符合三次曲线，也就是：$f(x)=a{x}^3+b{x}^2+cx+d$

也就是我们线性回归的目标是求出a,b,c,d

然而，sklearn.linear_model本身并不直接支持$x^n$次方，但是我们可以利用它支持多个特征的特性来完成三次曲线的拟合。

sklearn.linear_model支持多个特征。因此我们假设的模型函数为：$f(x_3,x_2,x_1)=a{x}_3+b{x}_2+c{x}_1+d$

其中该模型具有三个特征$x_3,x_2,x_1$。而实际我们只有一个特征$x$，因此我们需要利用$x$构造出三个特征，即：
$$\begin{array}{r}{x}_3=x^3\\ x_2=x^2\\ x_1=x\end{array}$$

通过这种方式，我们就巧妙利用linear_model多特征特性，解决了一个特征的多元线性回归。

4.1 利用PolynomialFeatures构造输入

sklearn提供了帮你构造$x_3,x_2,x_1$的方法sklearn.preprocessing.PolynomialFeatures。

我们先来尝试一下：

from sklearn.preprocessing import PolynomialFeaturesX_temp = np.arange(0, 3).reshape(-1, 1)
X_ = PolynomialFeatures(degree=3).fit_transform(X_temp)
print("X_temp:", X_temp.reshape(-1))
print("\nX_:\n", X_)

X_temp: [0 1 2]X_:[[1. 0. 0. 0.][1. 1. 1. 1.][1. 2. 4. 8.]]

上面的例子中，我们使用PolynomialFeatures(degree=3)对X_temp进行了处理。

其中X_temp是我们的输入，一共有3个样本[0, 1, 2]，每个样本有1个特征。经过PolynomialFeatures(degree=3).fit_transform(X_temp)处理后，我们得到了新的输入X_

X_同样是3个样本，但每个样本有4（3+1）个特征，通过观察很容易发现。这4个特征与原始的1个特征的关系为：$x^0,x^1,x^2,x^3$。

实际我们在使用时，其实不需要$x^0$，因为linear_model中的intercept_已经具备了$x^0$的功能，所以我们可以使用PolynomialFeatures(degree=3, include_bias=False)中的include_bias=False来去掉$x^0$

接下来我们对一开始的X进行一下处理：

X_p = PolynomialFeatures(degree=3, include_bias=False).fit_transform(X.reshape(-1, 1))

4.2 进行多元线性回归

对输入X处理后，接下来的线性回归过程和一元线性回归就没什么区别了：

model = linear_model.LinearRegression()
model.fit(X_p, y_label)

LinearRegression()

我们再来看下coef_和intercept_

print("model.coef_:", model.coef_)
print("model.intercept_:", model.intercept_)

model.coef_: [ 0.91962613  0.76846728 -0.49995355]
model.intercept_: 9.211345527598573

这次model.coef_一共有3个数值，分别对应$x^1,x^2,x^3$前面的系数。

我们先用模型的方式绘制一下预测结果：

plt.scatter(X, y_label, c='red')
plt.plot(X, model.predict(X_p), c='green')
plt.show()

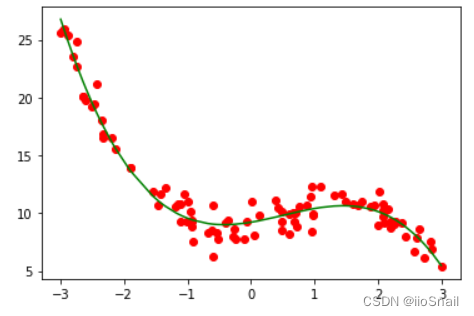
接下来我们再用公式的方式将结果绘制一下，公式为：y=ax+bx^2+cx^3+d

a = model.coef_[0]
b = model.coef_[1]
c = model.coef_[2]
d = model.intercept_
y_predict = a * X + b * X**2 + c * X**3 + dplt.scatter(X, y_label, c='red')
plt.plot(X, y_predict, c='green')
plt.show()

可以看到结果一致与模型结果一致

5. 总结

一元线性回归：

1. 线性回归需要使用model.linear_model的LinearRegression()方法
2. 一元线性回归需要将$X$reshape成(样本数, 1)的维度
3. 使用model.fit(X, y)进行模型拟合
4. model.coef_存储的是$x$前面的系数，model.intercept_存储的是截距

多元线性回归：

1. 多选线性回归需要使用PolynomialFeatures对X进行处理，它会将X转化为多个特征，分别对应$x^0,x^1,x^2,...$
2. 使用PolynomialFeatures的include_bias=False参数可以去掉$x^0$。建议使用
3. 对X处理后，后续的流程与一元线性回归一致
4. model.coef_存储了多个系数，分别为$x^0,x^1,x^2,...$前面的系数。model.intercept_存储的是截距