KL散度量化
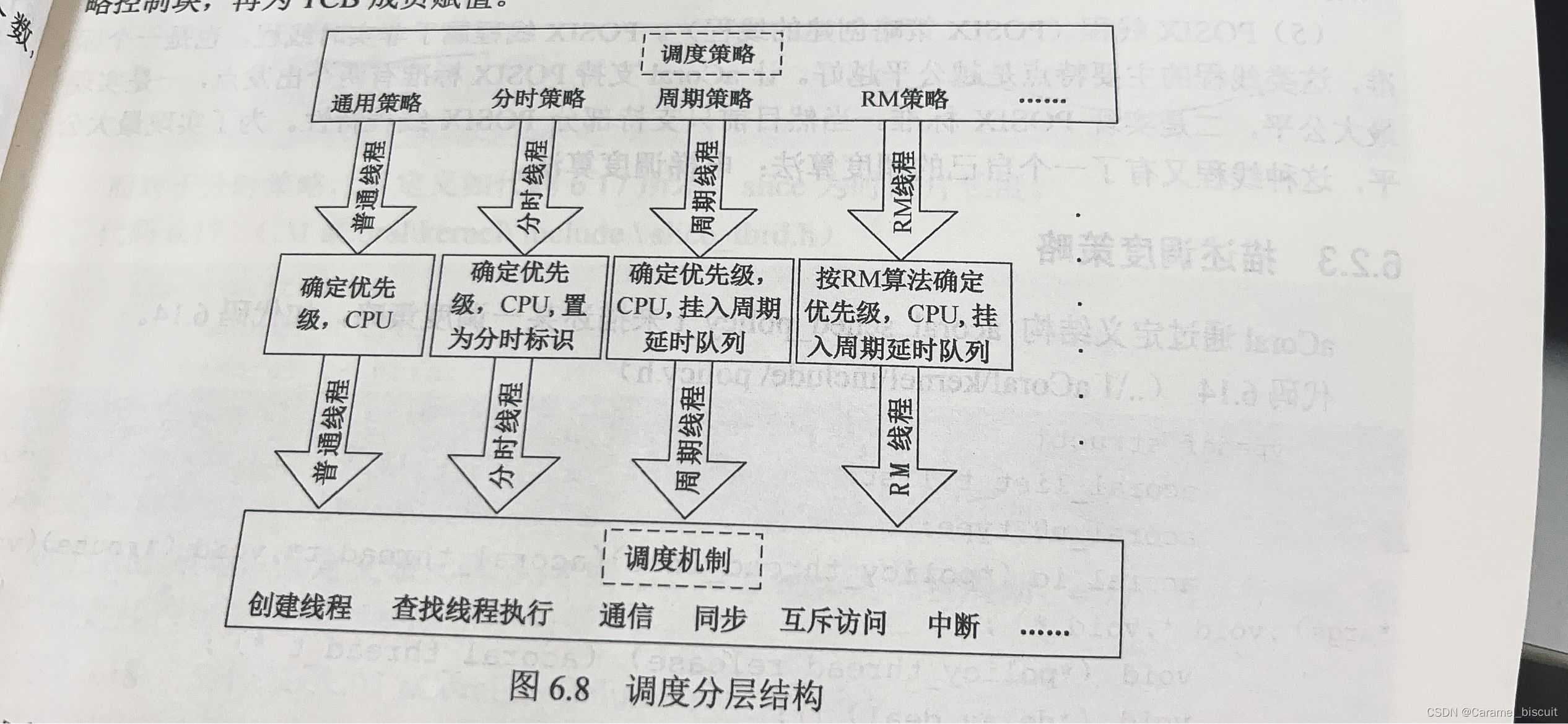
前面介绍的非对称量化中,是将数据中的min值和max值直接映射到[-128, 127]。
同样的,前面介绍的对称量化是将数据的最大绝对值 ∣ m a x ∣ |max| ∣max∣直接映射到127。
上面两种直接映射的方法比较粗暴,而TensorRT中的int8量化是基于KL散度来选取最佳的阈值T来映射到127中。超出阈值 ± ∣ T ∣ \pm|T| ±∣T∣的数据会直接映射为阈值(类似于截断映射)。
KL散度定义
KL散度常用来衡量两个分布P和Q之间的差异,KL散度越小,两个分布越相似,其公式定义如下:
D K L = ∑ i P ( x i ) l o g ( P ( x i ) Q ( x i ) ) D_{KL} = \sum_{i}P(x_i)log(\frac{P(x_i)}{Q(x_i)}) DKL=i∑P(xi)log(Q(xi)P(xi))
TensorRT实现KL散度量化的步骤
- 基于原始输入数据生成拥有2048个bin的直方图
hist, bin_edges = np.histogram(P, bins = 2048)
- 在[128, 2048]返回内循环执行3-5步,寻找最佳的划分 b i n i bin_{i} bini
- [ 0 , b i n i ] [0,bin{i}] [0,bini]范围内的直方图数据作为原始P, 并将 b i n i bin_{i} bini之后的直方图数据进行求和,并累加到 b i n i − 1 bin_{i-1} bini−1中形成以 b i n i bin_{i} bini作为划分的最终P分布
- 对P分布进行量化形成Q分布(一般是划分和合并bins,计算合并后的平均值作为Q分布对应bins的值)

- 计算P分布和Q分布的KL散度
- 根据最小的KL散度来选取最佳的 b i n b e s t bin_{best} binbest,将bin_edges[ b i n b e s t bin_{best} binbest]作为最终的阈值threshold,即映射到127的阈值T
- 根据最佳的阈值T来计算scale
s c a l e = T i n t m a x = T 127 scale = \frac{T}{int_{max}} = \frac{T}{127} scale=intmaxT=127T - 根据对称量化来量化原始数据(权重、激活值等等)
TensorRT使用KL散度量化的目的
通过KL散度选取合适的阈值T,根据阈值计算对应的缩放系数scale,力求int8量化后的数值能更准确表示出量化前的FP32数值。
代码案例
import random
import numpy as np
import matplotlib.pyplot as plt
import copy
import scipy.stats as stats# 随机生成测试数据
def generator_P(size):walk = []avg = random.uniform(3.000, 600.999)std = random.uniform(500.000, 1024.959)for _ in range(size):walk.append(random.gauss(avg, std)) # 生成符合高斯分布的随机数return walk# 平滑p和q,防止出现nan值,因为KL散度会计算log(p/q), 当q为0值时会出现nan
def smooth_distribution(p, eps=0.0001):is_zeros = (p == 0).astype(np.float32)is_nonzeros = (p != 0).astype(np.float32)n_zeros = is_zeros.sum()n_nonzeros = p.size - n_zerosif not n_nonzeros:raise ValueError('The discrete probability distribution is malformed. All entries are 0.')eps1 = eps * float(n_zeros) / float(n_nonzeros)assert eps1 < 1.0, 'n_zeros=%d, n_nonzeros=%d, eps1=%f' % (n_zeros, n_nonzeros, eps1)hist = p.astype(np.float32)hist += eps * is_zeros + (-eps1) * is_nonzerosassert (hist <= 0).sum() == 0return histdef threshold_distribution(distribution, target_bin = 128):distribution = distribution[1:]length = distribution.size # 2047threshold_sum = sum(distribution[target_bin:]) # [128: ]kl_divergence = np.zeros(length - target_bin) # 初始化 2047 - 128 = 1919 个KL散度值for threshold in range(target_bin, length): # 遍历threshold寻找KL散度最低的阈值sliced_nd_hist = copy.deepcopy(distribution[:threshold]) # [0, threshold)内的作为Pp = sliced_nd_hist.copy() # 生成pp[threshold - 1] += threshold_sum # 把 [threshold:] 后的累加和加到 p[threshold - 1] 中threshold_sum = threshold_sum - distribution[threshold] # 更新下一轮的累加和,即上一轮的累加和减去即将移入P分布的区间数据is_nonzeros = (p != 0).astype(np.int64) # [0:threshold]内不为0的区间quantized_bins = np.zeros(target_bin, dtype = np.int64) # 初始化量化后的binsnum_merged_bins = sliced_nd_hist.size // target_bin # 计算多少个区间需要合并来计算平均值,例如最初有8个bins,需要合并到4个bins,则每两个bins需要进行合并# 合并binsfor j in range(target_bin): start = j * num_merged_bins # 合并开始的binsstop = start + num_merged_bins # 合并结束的binsquantized_bins[j] = sliced_nd_hist[start:stop].sum() # 计算区间内bins的总和quantized_bins[-1] += sliced_nd_hist[target_bin * num_merged_bins:].sum()# 计算qq = np.zeros(sliced_nd_hist.size, dtype = np.float64) # 初始化量化后的qfor j in range(target_bin):start = j * num_merged_binsif j == target_bin - 1:stop = -1else:stop = start + num_merged_bins # 每num_merged_bins个bins进行合并组成qnorm = is_nonzeros[start:stop].sum() # 看看合并区间里,不为0的区间个数if norm != 0:q[start:stop] = float(quantized_bins[j]) / float(norm) # 用均值(假如区间内都不为0)填充q# 平滑p和qp = smooth_distribution(p)q = smooth_distribution(q)# 计算p和q之间的KL散度kl_divergence[threshold - target_bin] = stats.entropy(p, q)# 寻找最小KL散度对应threshold的索引min_kl_divergence = np.argmin(kl_divergence)threshold_value = min_kl_divergence + target_bin # 计算真正的threshold, 基于最初的128, 因为一开始就是从128开始不断向外计算来扩大P的范围return threshold_valueif __name__ == '__main__':# 随机初始化测试数据size = 20480 P = generator_P(size) P = np.array(P)P = P[P > 0] # 保留大于0的数# print("maximum activation value", max(np.absolute(P))) # 最大的激活值hist, bin_edges = np.histogram(P, bins = 2048) # 生成直方图 hist表示每一个bins对应的数量, bins表示截止 threshold = threshold_distribution(hist, target_bin = 128) # 返回KL散度最小的划分binsprint("threshold: ", threshold)print("threshold edges:", bin_edges[threshold]) # 截止到threshold对应的bins, 能够表示的范围 bin_edges[-1]表示上面最大的激活值,即能够表示所有数# 计算scale# scale = bin_edges[threshold] / int_max # 即bin_edges[threshold] / 127 # 在最初的对称量化中,我们是用绝对值最大的数值作为bin_edges[threhold], 而TensorRT就是利用KL散度来评估最佳的bin_edges[threshold]# 分成 split_zie 组, density表示是否要normedplt.title("Relu activation value Histogram")plt.xlabel("Activation values")plt.ylabel("Normalized number of Counts")plt.hist(P, bins=2047)plt.vlines(bin_edges[threshold], 0, 30, colors = "r", linestyles = "dashed") # 红线向左就是能够表示的所有范围plt.show()