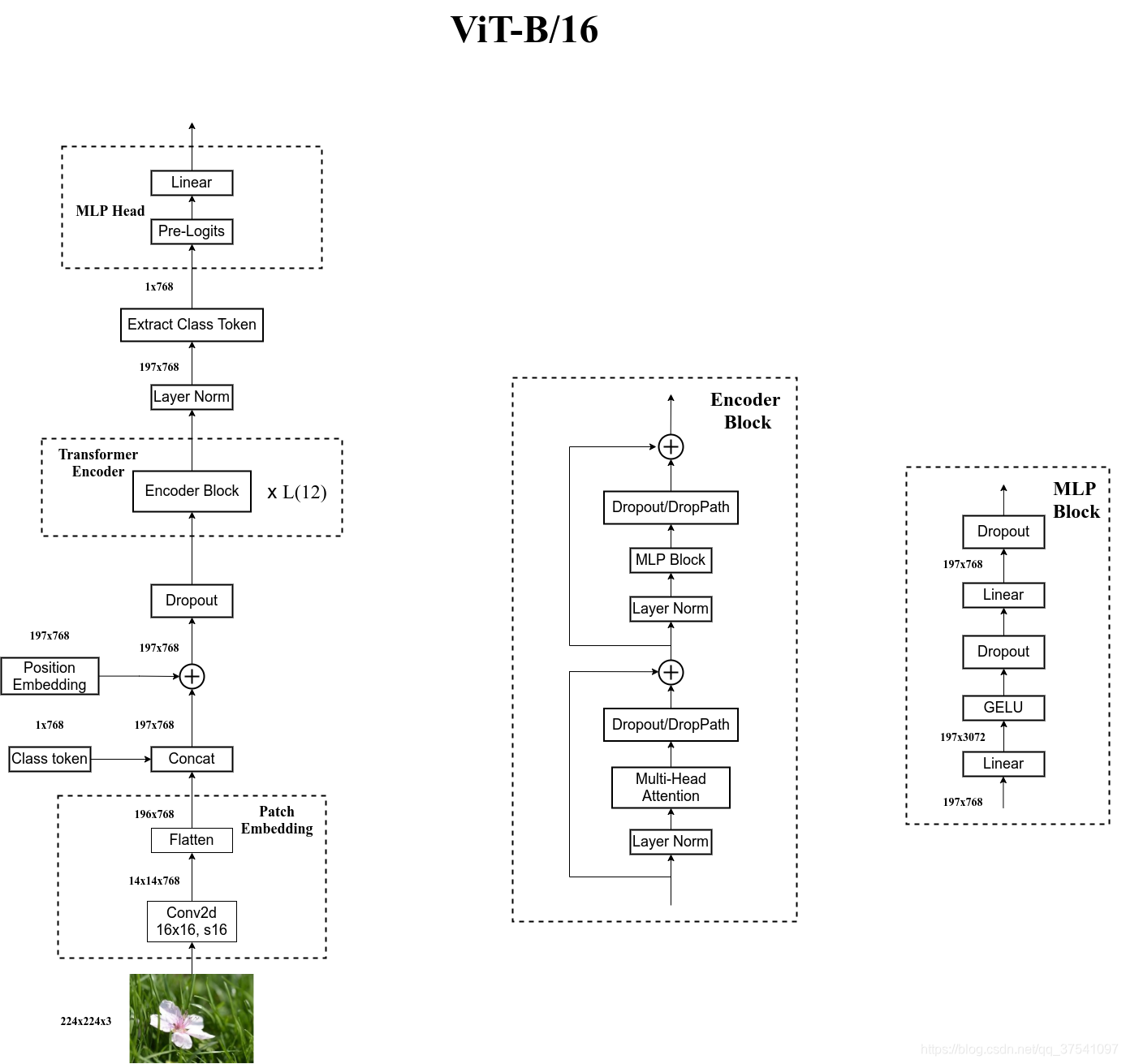
【海量数据挖掘/数据分析】之决策树模型（决策树模型、决策树构成、决策树常用算法、决策树性能要求、信息增益、信息增益计算公式、决策树信息增益计算实例）

一、决策树模型

1、常用算法

2、属性划分策略

3、其他算法

三、决策树算法性能要求

四、决策树模型创建 ( 递归创建决策树 )

1 、决策树模型创建

2 、决策树创建算法 ( 递归 )

3 、递归操作

4 、递归停止的条件

五、决策树树根属性选择

六、信息增益说明

1、熵和信息的数据组成

2 、信息增益分析

3、信息增益计算步骤

4、信息增益计算使用的数据集 S

七、信息增益计算公式

1 、已知条件 ( 变量声明 ) : 声明一些计算公式中使用的变量说明

2、信息增益总熵计算公式

3、信息增益每个属性的熵计算公式

4、信息增益计算公式

八、信息增益计算实例

1 、已知数据

2 、总熵计算 :

3、计算年龄属性的熵 :

4、计算年龄属性不同样本取值的熵 :

5、计算年龄属性的信息增益

6、依次计算各个属性的熵 :

九、信息增益计算递归确定划分属性

一、决策树模型

1 、决策树 : 决策时基于 “树” 结构 , 这也是模拟人在进行决策时采用的策略 ;

2、决策树组成 : 根节点 , 内部节点 , 叶子节点 , 这些节点都是数据的属性 ( 特征 ) ;

根节点 : 最初始判定的属性 , 判定区域是全局的数据集 ;
内部节点 : 中间的判定属性 , 判定区域是符合某些特征的子数据集 ;
叶子节点 : 决策结果 , 位于决策树的最底层 , 每个叶子节点都是一个决策结果 ;

3、决策树模型过程

① 训练过程 : 使用训练集数据确定决策时使用的属性 , 确定根节点 , 内部节点 , 叶子节点的属性划分 , 训练决策树模型 ;

② 预测过程 : 从根节点特征开始 , 根据决策树中的判定序列依次从根节点向下判定 , 直到一个叶子节点 ;

4、实例说明

1 ） 需求场景 :

① 需求 : 电商网站为用户进行分类 , 目的是确定该用户是否有可能购买某件商品 , 然后为其推送指定商品的广告 ;

② 决策树使用 : 如何对用户进行分类 , 这里就用到了决策树模型 , 将用户分成不同的类别 ;

2 ） 数据集 : 决策过程中 , 根据每个节点所处理的数据集的特征 , 将其划分到不同的子节点中进行处理 ; 如数据集中是 100 个用户的信息 ;

3 ） 决策树构成 :

① 根节点决策 : 根节点处理年龄特征 , 小于 30 岁的用户划分到一组 , 大于 30 岁的用户划分到另一组 ;

② 内部节点决策 : 然后在小于 30 岁的用户中继续判定 , 学生划分成一组 , 非学生划分成一组 ;

③ 叶子节点决策结果 : 学生会买电脑 , 非学生不会买电脑 ;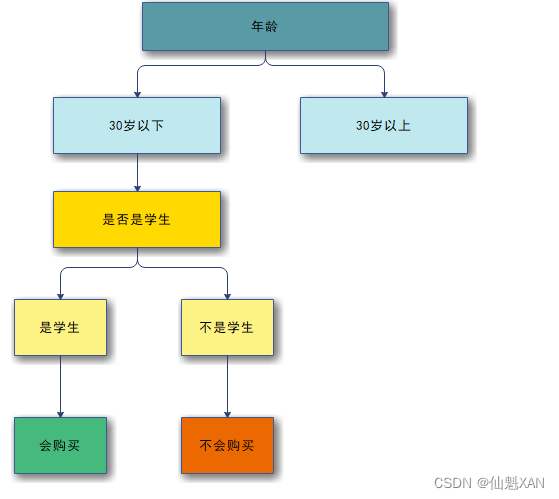

二、常用的决策树算法

1、常用算法

CLS 算法 : 这是第一个决策树算法 , 1966 年提出 ;
ID3 算法 : 该算法使决策树称为机器学习主流技术 , 1979 年提出 ;
C4.5 算法 : 最常用的决策树算法 ; 1993 年提出 ;

区别 : 上述三个算法五个组件基本一致 , 唯一的区别是确定属性划分时的策略不同 , 即将哪个属性放在树根 , 将哪个属性放在内部节点上 , 内部节点的属性所在层级如何设置 ;

2、属性划分策略

① ID3 算法属性划分策略 : ID3 使用信息增益策略 ;

② C4.5 算法属性划分策略 : C4.5 使用的是增益率策略 ;

3、其他算法

1) CART 算法 : 既可以用于分类任务 ( 结果是离散值 ) , 也可以用于回归任务 ( 结果是连续值 ) ;

2) FR 算法 : 随机森林算法 ; 使用了数据挖掘 , 机器学习中的集成思想 ; 有很多差的分类器 , 准确率都很低 , 但是多个分类器集成起来 , 准确率就很高 ;

三、决策树算法性能要求

1 、决策树的高度 :

① 决策树最大高度 : 决策属性的个数 ; ( 每个属性都要决策一次 , 才能预测出结果 )

② 决策时最小高度 : 1 ; ( 只需要决策一次 , 就可以预测出结果 )

2 . 决策树性能 : 决策树越矮越好 , 即预测某特征 , 进行的决策次数越少越好 ;

3 . 树根属性 : 越重要的属性 , 其越能将数据最大可能拆分开 , 将重要的属性放在树根 ;

四、决策树模型创建 ( 递归创建决策树 )

1 、决策树模型创建

决策树模型创建的核心就是选择合适的树根 , 将重要的属性放在树根 , 然后子树中 , 继续选择子树中重要的属性放在子树的树根 , 依次递归 , 最终得到决策结果 ( 叶子节点 ) ;

2 、决策树创建算法 ( 递归 )

使用递归算法 , 递归算法分为递归操作和递归停止条件 ;

3 、递归操作

每个步骤先选择属性 , 选择好属性后 , 根据总树 ( 子树 ) 的树根属性划分训练集 ;

① 选择属性 : 递归由上到下决定每一个节点的属性 , 依次递归构造决策树 ;

② 数据集划分 : 开始决策时 , 所有的数据都在树根 , 由树根属性来划分数据集 ;

③ 属性离散化 : 如果属性的值是连续值 , 需要将连续属性值离散化 ; 如 : 100 分满分 , 将 60 分以下分为不及格数据 , 60 分以上分为及格数据 ;

4 、递归停止的条件

① 子树分类完成 : 节点上的子数据集都属于同一个类别 , 该节点就不再向下划分 , 称为叶子节点 ;

② 属性 ( 节点 ) 全部分配完毕 : 所有的属性都已经分配完毕 , 决策树的高度等于属性个数 ;

③ 所有样本分类完毕 : 所有的样本数据集都分类完成 ;

五、决策树树根属性选择

1 . 属性选择方法 : 树根属性选择的方法很多 , 这里介绍一种常用的方法 , 信息增益 ;

2 . 信息增益 : 信息增益效果越大 , 其作为树根属性 , 划分的数据集分类效果越明显 ;

3 . 信息和熵

① 信息与熵的关系 : 信息会消除熵 , 熵代表了不确定性 , 信息用来消除不确定性 ;

② 信息增益 : 信息增益大的属性 , 能最大消除熵的不确定性 ;

4 . 决策树中的信息增益 : 属性的信息增益越大 , 就越能将分类效果达到最大 ;

如 : 想要从用户数据集中找到是否能买奢侈品的用户 , 先把高收入群体划分出来 , 将低收入者从数据集中去除 , 这个收入水平的属性 ( 特征 ) , 信息增益就很大 ;

六、信息增益说明

1、熵和信息的数据组成

① 数据集 ( 熵 ) : 给定一个总的数据集如 100 个用户数据 , 要从里面选择购买奢侈品的 1 个用户 ( 高收入 , 30 岁以下 ) ;

② 年龄属性 ( 信息 ) : 30 岁以上的 50 个 , 30 岁以下的 50 个 ;

③ 收入属性 ( 信息 ) : 高收入 10 个 , 低收入 90 个 ;

2 、信息增益分析

① 收入属性的信息增益 : 熵是 100 个用户数据 , 代表不确定性 ; 根据收入属性来划分 , 将高收入者 10 个用户划分出来 , 买奢侈品的用户从这 10 个中选择 ; 由 100 个用户中选 1 个用户 , 变为 10 个用户中选择 1 个用户 ; 消除了 90 个用户的不确定性 ;

② 年龄属性的信息增益 : 熵是 100 个用户数据 , 代表不确定性 ; 根据收入属性来划分 , 将30 岁以下的 50 个用户划分出来 , 买奢侈品的用户从这 50 个中选择 ; 由 100 个用户中选 1 个用户 , 变为 50 个用户中选择 1 个用户 ; 消除了 50 个用户的不确定性 ;

③ 信息增益分析 : 明显收入属性的信息增益要高于年龄属性的信息增益 ;

3、信息增益计算步骤

1 ）总熵 : 不考虑输入变量 ( 属性 / 特征 ) , 为数据集 S 中的某个数据样本进行分类 , 计算出该过程的熵 ( 不确定性 ) , 用 Entropy(S) 表示 ;

2 ）引入属性后的熵 : 使用输入变量 ( 属性 / 特征 ) X 后 , 为数据集 S 中的某个数据样本进行分类 , 计算出该过程的熵 ( 不确定性 ) , 用 Entropy(X , S) 表示 ;

3 ）信息增益 : 上面 Entropy(X , S) - Entropy(S) 的差 , 就是 X 属性 ( 特征 ) 带来的信息增益 , 用 Gain(X , S) 表示 ;

4、信息增益计算使用的数据集 S

数据集 : 根据年龄 , 收入水平 , 是否是学生 , 信用等级 , 预测该用户是否会购买商品 ;如下图

① 是否会购买商品 : 9 个会购买 , 5 个不会购买 ;

② 年龄 ( 属性 ) :

5 个小于 30 岁的人中 , 3 个不会买电脑 , 有 2 个会买商品 ;

4 个 31 ~ 39 岁的人中 , 0 个不会买电脑 , 有 4 个会买商品 ;

5 个大于 40 岁的人中 , 2 个不会买电脑 , 有 3 个会买商品 ;

七、信息增益计算公式

数据集如下图：

1 、已知条件 ( 变量声明 ) : 声明一些计算公式中使用的变量说明

① 总的数据集 : S

② 最终分类个数 : m , 最终分成 m 个类别 , 如是否购买商品 ( 是 , 否 ) , 就是分成 2 类 , m = 2 ;

③ 分类表示 : C i ( i = 1 , ⋯ , m ) , 如 : 是否购买商品 ( 是 , 否 ) , C1 表示是 , C2 表示否 ;

④ 分类样本个数 : s i ( i = 1 , ⋯ , m ) , 如 : 是否购买商品 , 会购买的 ( C1 ) 的样本个数是 9 人 , 表示为 s1=9 ;

2、信息增益总熵计算公式

① 加和式 : 这是一个 1 到 m 加和式 ;

② 比值权重 : s/si 表示第i 个样本数 ( si ) 与总样本数 ( s) 比值 ;

示例说明

① 需求 : 判定 14 个用户是否会购买某商品 , 9 个会购买 , 5 个不购买 ;

② 计算过程 :

3、信息增益每个属性的熵计算公式

1 ）计算熵的属性 : 属性 A 的值为 {a1,a2,⋯,av} ;

2 ）引入属性 ( 特征 ) A 后的熵计算公式 :

3）公式解析 :

① 剩余的熵 : 引入属性 A 后 , 属性 A 是信息 , 信息会消除熵 , 这里计算消除后剩余的熵是多少 ;

② 属性解析 : 这是一个 1 到 v 的加和式 , v 表示 A 属性的取值个数 ,

如 : A 表示年龄 , 有 : 30岁以下( a1 ) 有 5 个样本 , 31 ~ 39 岁 ( a2 ) 有 4 个样本 , 40 岁以上( a3 ) 有 5 个样本 , 所以 v = 3 ;

③ 系数说明 : 其中 Sj / S 系数表示 , 属性 A ( 年龄特征 ) 的第 j 个版本的比例 , 这个比例越高 , 样本对多 , 越重要 ;

4）属性的熵示例说明

简单说明计算过程解析

① 5/14*Entropy(2,3) 在 5 个小于 30 岁的人中 , 有 2 个会买商品 , 3 个不会买商品 ;
② 4/14*Entropy(4,0) 在 4 个 31 ~ 39 岁的人中 , 有 4 个会买商品 , 0 个不会买商品 ;
③ 5/14*Entropy(3,2) 在 5 个大于 40 岁的人中 , 有 3 个会买商品 , 2 个不会买商品 ;

4、信息增益计算公式

计算 A A A 属性的信息增益 :

八、信息增益计算实例

数据列表如下：

1 、已知数据

① 数据集 : 计算上述数据集 S 的信息增益 , 该数据集 S 有 14 个样本数据 ;

② 数据集属性 : 数据集 S 有 5 个属性 , 年龄 , 收入 , 是否是学生 , 信用等级 , 是否购买商品 ;

③ 预测属性 : 根据年龄 , 收入 , 是否是学生 , 信用等级 4 个属性 , 预测是否购买商品这个属性 ;

2 、总熵计算 :

① 总熵 : 计算每个属性的信息增益 , 先要使用 Entropy(S) 公式计算出总熵 ;

① 预测属性分析 : 最后预测的属性是是否购买电脑 , 有两个取值 , 是或否 , 2 个取值 , 计算总熵时 , 需要计算两项 , 分别计算取值会买电脑和不会买电脑的熵 ;

③ 属性的具体分类 : 判定 14 个用户是否会购买某商品 , 9 个会购买 , 5 个不购买 ;

④ 计算过程 :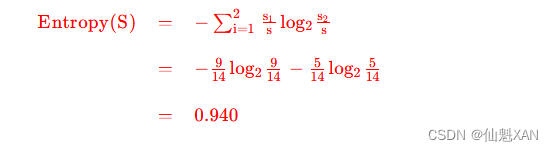

3、计算年龄属性的熵 :

① 引入属性 : 引入年龄属性后 , 年龄属性是信息 , 信息会消除熵 , 这里计算引入年龄属性之后的熵是多少 ;

② 年龄属性分析 : 年龄属性有 3 种取值 : 30岁以下有 5 个样本 , 31 ~ 39 岁有 4 个样本 , 40 岁以上有 5 个样本 ;

③ 计算内容 :

需要分别计算 3 种取值的熵各是多少 ,

30岁以下有 5 个样本 , 需要计算这 5 个样本的熵是多少 , 5 个样本 , 有 3 个人买商品 , 2 个人不买商品 ,

④ 计算示例 :

5/14 * Entropy(2,3) 在 5 个小于 30 岁的人中 , 有 2 个会买商品 , 3 个不会买商品 ;
4 /14 * Entropy(4,0) 在 4 个 31 ~ 39 岁的人中 , 有 4 个会买商品 , 0 个不会买商品 ;
5/ 14 * Entropy(3,2) 在 5 个大于 40 岁的人中 , 有 3 个会买商品 , 2 个不会买商品 ;

4、计算年龄属性不同样本取值的熵 :

① 计算 Entropy(2 , 3) : 5 个人 , 有 2 个人买商品 , 3 个人没有买商品 ;

② 计算 Entropy(4,0) : 4 个人 , 有 4 个人买商品 , 0 个人没有买商品 ;

③ 计算 Entropy(3 , 2) : 5 个人 , 有 3 个人买商品 , 2 个人没有买商品 ;

5、计算年龄属性的信息增益

6、依次计算各个属性的熵 :

① 年龄属性的信息增益 : Gain ( 年龄 ) = 0.246

② 收入属性的信息增益 : Gain ( 收入 ) = 0.029

③ 是否是学生属性的信息增益 : Gain ( 是否是学生 ) = 0.151

④ 信用等级属性的信息增益 : Gain ( 信用等级 ) = 0.048

⑤ 树根属性选择: 年龄属性的信息增益最大 , 选择年龄属性作为树根 ;

后续工作 ( 重要 ) : 选择完树根后 , 树根属性将数据分为不同的子集 , 每个子集再计算剩余的 3 个属性 , 哪个属性的信息增益最大 , 就选那个属性作为子树的树根属性 ;

九、信息增益计算递归确定划分属性

1 . 计算公式使用 : 根据上述公式 , 计算出每个属性的信息增益 , 递归选取信息增益最大的作为树根

2 . 决策树创建算法 ( 递归 ) : 使用递归算法 , 递归算法分为递归操作和递归停止条件 ;

3 . 递归操作 : 每个步骤先选择属性 , 选择好属性后 , 根据总树 ( 子树 ) 的树根属性划分训练集 ;

① 选择属性 : 递归由上到下决定每一个节点的属性 , 依次递归构造决策树 ;

② 数据集划分 : 开始决策时 , 所有的数据都在树根 , 由树根属性来划分数据集 ;

③ 属性离散化 : 如果属性的值是连续值 , 需要将连续属性值离散化 ; 如 : 100 分满分 , 将 60 分以下分为不及格数据 , 60 分以上分为及格数据 ;

4 . 递归停止的条件 :

① 子树分类完成 : 节点上的子数据集都属于同一个类别 , 该节点就不再向下划分 , 称为叶子节点 ;

② 属性 ( 节点 ) 全部分配完毕 : 所有的属性都已经分配完毕 , 决策树的高度等于属性个数 ;

③ 所有样本分类完毕 : 所有的样本数据集都分类完成 ;

5 . 下图是最终的决策树样式 :

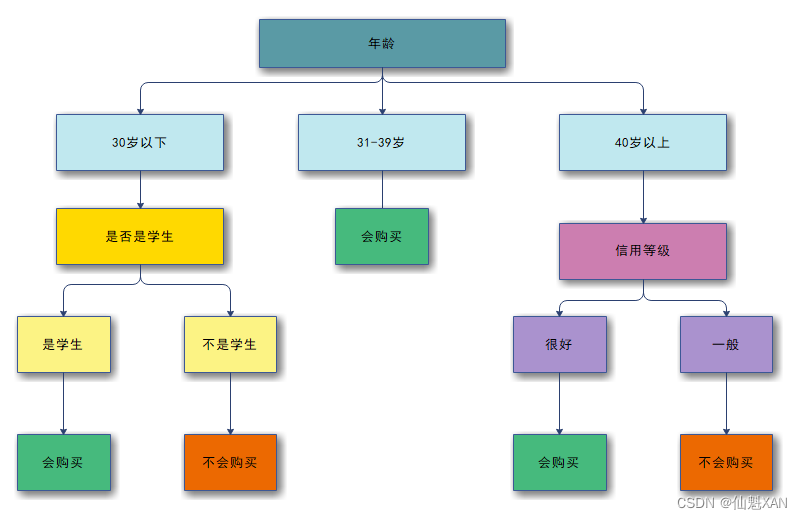
参考博文：

【数据挖掘】决策树算法简介 ( 决策树模型 | 模型示例 | 决策树算法性能要求 | 递归创建决策树 | 树根属性选择 )_讨论决策树属性选择的原则和要求

【数据挖掘】决策树中根据信息增益确定划分属性 ( 信息与熵 | 总熵计算公式 | 每个属性的熵计算公式 | 信息增益计算公式 | 划分属性确定 )_数据挖掘决策树划分信息熵信息增益