时间、空间复杂度的例题详解-编程知识

文章前言

上篇文章带大家认识了数据结构和算法的含义，以及理解了时间、空间复杂度，那么接下来来深入理解一下时间、空间复杂度。

时间复杂度实例

实例1

// 计算Func2的时间复杂度？
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}

很明显可以知道是2*N+10，所以时间复杂度为O(n)。

实例2

// 计算Func3的时间复杂度？
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}

运行次数是N+M，时间复杂度为 O(N+M)

实例3

// 计算Func4的时间复杂度？
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}

在这里面进行了100次循环和N没有关系，所有时间复杂度为O（1）

实例4

// 计算strchr的时间复杂度？
const char * strchr ( const char * str, int character );

大家如果不了解strchr函数，可以大概看一下介绍：
strchr 函数是一个 C 标准库中的字符串函数，用于从字符串中查找指定字符的第一次出现位置，它的函数原型为：

char *strchr(const char *s, int c);

该函数的内部构造实现并不是特别复杂，它的实现可以分为以下几个步骤：
检验输入参数是否合法，若非法则返回 NULL。其中，参数 s 表示需要查找的字符串，参数 c 表示需要查找的字符。

if (s == NULL)return NULL;

遍历字符串 s，查找字符 c 的出现位置，若找到则返回该位置的指针。若未找到则返回 NULL。

while (*s != '\0') {if (*s == (char)c)return (char *)s;s++;
}
return NULL;

上述代码使用了一个 while 循环，遍历字符串中的每个字符，检查当前字符是否等于指定字符 c。一旦找到了第一次出现 c 的位置，就立即返回该位置的指针。如果遍历完整个字符串后仍未找到指定字符，则最终返回 NULL。

综上所述，strchr 函数的内部构造并不复杂，主要是遍历字符串查找目标字符的过程。需要注意的是，由于该函数返回的是指针类型，因此需要进行类型转换。

所以，我们可以很容易的根据时间复杂度的定义：基本操作执行最好1次，最坏N次，时间复杂度一般看最坏，时间复杂度为 O(N)。

实例5

// 计算BubbleSort的时间复杂度？
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

基本操作执行最好N次，最坏执行了(N*(N+1)/2次，通过推导大O阶方法+时间复杂度一般看最坏，时间复杂度为 O(N^2)。

实例6

// 计算BinarySearch的时间复杂度？
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]：begin和end是左闭右闭区间，因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}

我们可以知道这是一个二分查找，二分查找是一个很厉害的算法，他的效率特别高。基本操作执行最好1次，最坏O(logN)次，时间复杂度为 O(logN) （ps：logN在算法分析中表示是底数为2，对数为N。有些地方会写成lgN。）

实例7

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}

可以很简单的知道执行次数是N+1次，那么时间复杂度为O（n）。

实例8

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}

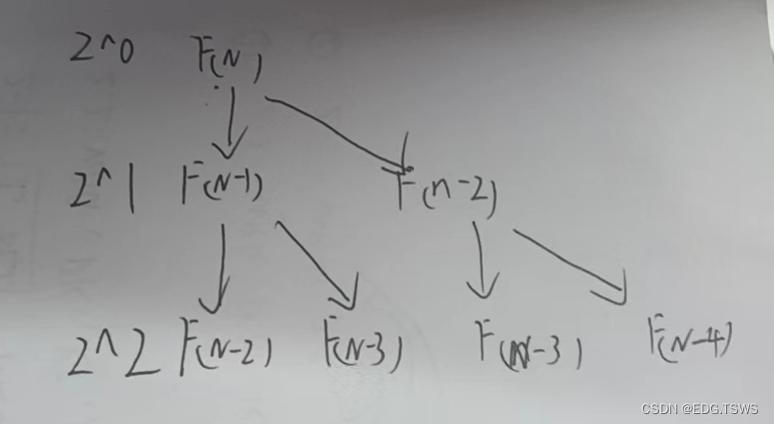
在这里插入图片描述

大概也就是（1/2）*2^N-1，所以时间复杂度就为O(2^N)。

空间复杂度实例

实例1

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

仅使用了常数个额外空间，所以空间复杂度为O(1)。

实例2

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}

该代码动态开辟了N个空间，所以空间复杂度为O(N)。

实例3

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}

递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N）。

根据时间、空间复杂度解题

消失的数字

问题描述：
数组nums包含从0到n的所有整数，但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗？
这里给大家把链接奉上，可以先挑战一下试试。

https://leetcode-cn.com/problems/missing-number-lcci/

思路分析：
首先很简单的做法是暴力遍历，但是效率不够高，可能会超时，所以这种做法可行只要不出问题都可以作出来，就不再过多赘述。
思路一：
从0到n，丢失了一个数字，我们可以把从0到n的数字先全部加起来，之后用这个值减去所有的数字，就可以知道这个丢失的数字是多少了。

int missingNumber(int* nums, int numsSize) {int N = numsSize;//用N来记录方便代码书写int sum = ((0 + N) * (N + 1)) / 2;//等茶树列前n项和for (int i = 0; i < N; i++)//减值循环{sum = sum - nums[i];}return sum;//返回值为sum即为丢失的数字。
}

在这里插入图片描述
该题解代码时间复杂度为O（N），空间复杂度为O（1）。
在这里是可以通过的，我们具体解释看注释。

思路二：我们之前学过异或符号，得到了一个结论相同为0，相异为1。那么我们就可以得到两个相同的数字异或起来得到的值就是0。0异或任何数字又都是该数字，那么我们就可以让0去异或从0到n，再去异或所有的数，最后得到的值就是丢失的那个数字。

int missingNumber(int* nums, int numsSize)
{int N = numsSize;//N来记录方便代码书写int F = 0;//定义F为0，用来异或for (int i = 0; i <= N; i++)//异或从0到n的所有数字循环{F ^= i;}for (int i = 0; i < N; i++)//再去异或所有数字的循环{F ^= nums[i];}return F;//得到的F即为丢失的数字返回即可。
}

在这里插入图片描述
该题解代码同样是时间复杂度为O（N），空间复杂度为O（1）。
可以看到在这里是通过的，具体解释请看代码。

移除元素

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。
不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
链接给大家奉上可以先尝试一下：

https://leetcode.cn/problems/remove-element/

题解思路：已经规定不能使用额外空间，那么我们可以用双指针的方法来解这道题目。

int removeElement(int* nums, int numsSize, int val){int src=0;//快指针（下标）int dst=0;//慢指针（下标）while(src<numsSize)//移除循环{if(nums[src]!=val)//快指针遍历，若不等于移除值，将快指针指向值赋给慢指针{nums[dst]=nums[src];dst++;src++;}else//除不相等情况，为相等情况，快指针直接遍历过去{src++;}}return dst;//返回新数组长度。
}

在这里插入图片描述
在这里，时间复杂度是O（N），空间复杂度为O（1）。
具体代码解释请看注释。

删除有序数组中的重复项

给你一个非严格递增排列的数组 nums ，请你原地删除重复出现的元素，使每个元素只出现一次，返回删除后数组的新长度。元素的相对顺序应该保持一致。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：

更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
链接奉上：

https://leetcode.cn/problems/remove-duplicates-from-sorted-array/description/

int removeDuplicates(int* nums, int numsSize) {int j=1;//快指针遍历int i=1;//慢指针记录for(j=1;j<numsSize;j++)//移除循环{if(nums[j]!=nums[i-1])//快指针遍历值不等于前一项慢指针记录值时//将该快指针指向值赋值给慢指针当前项值//相等情况快指针直接遍历过去{nums[i]=nums[j];i++;}}return i;
}

在这里同样用双指针方法，时间复杂度为O（N），空间复杂度为O（1）。

合并两个有序数组

给你两个按非递减顺序排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你合并 nums2 到 nums1 中，使合并后的数组同样按非递减顺序排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。
链接给大家奉上：

https://leetcode.cn/problems/merge-sorted-array/description/

int compar(const void* e1,const void* e2)
{return (*(int*)e1-*(int*)e2);
}
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){int i=0;int j=0;for(i=m;i<m+n;i++){nums1[i]=nums2[j];j++;}qsort(nums1,m+n,sizeof(int),compar);
}