数据结构–由遍历序列构造二叉树

不同二叉树的中序遍历序列

中序遍历:中序遍历$左$子树、$根$结点、中序遍历$右$子树

中序遍历序列:BDCAE

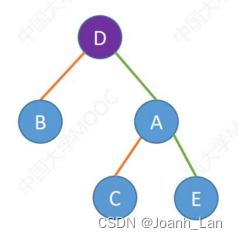
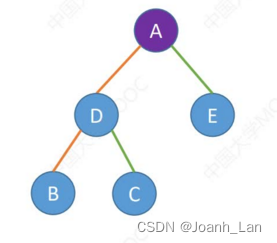
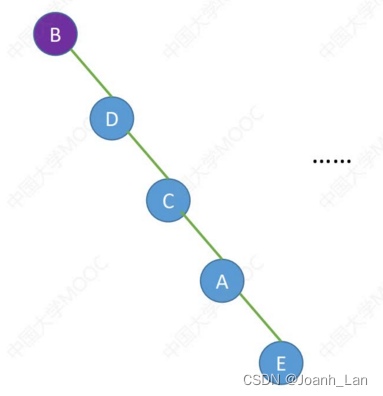
$结论:一个中序遍历序列可能对应多种二叉树形态$

不同二叉树的前序遍历序列

前序遍历:$根$结点、前序遍历$左$子树、前序遍历$右$子树

前序遍历序列:BDCAE

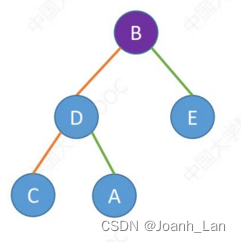
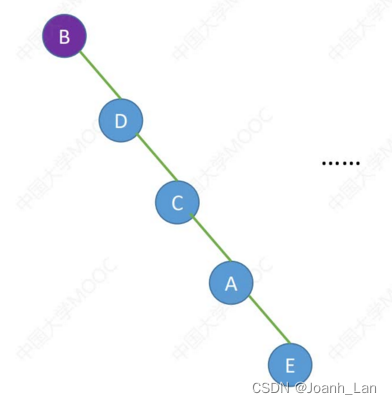
$结论:一个前序遍历序列可能对应多种二叉树形态$

不同二叉树的后序遍历序列

后序遍历:前序遍历$左$子树、前序遍历$右$子树、$根$结点

后序遍历序列:BDCAE

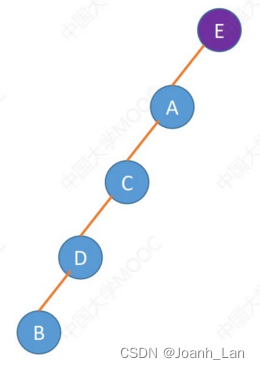
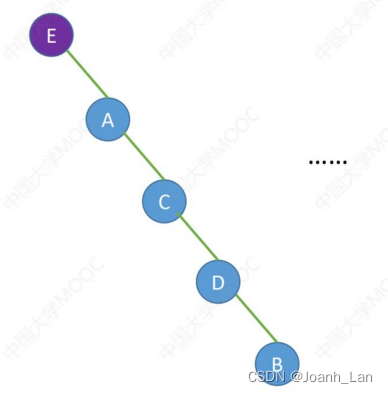
$结论:一个后序遍历序列可能对应多种二叉树形态$

不同二叉树的层序遍历序列

层序遍历序列:BDCAE

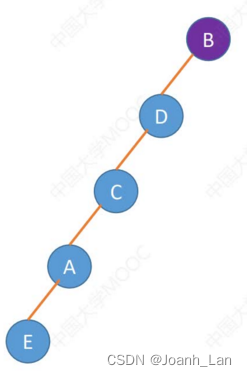
$结论:一个层序遍历序列可能对应多种二叉树形态$

$结论:若只给出一棵二叉树的前/中/后/层序遍历序列中的一种，不能唯一确定一棵二叉树$

前序＋中序遍历序列

前序遍历:$根$结点、前序遍历$左$子树、前序遍历$右$子树
中序遍历:中序遍历$左$子树、$根$结点、中序遍历$右$子树

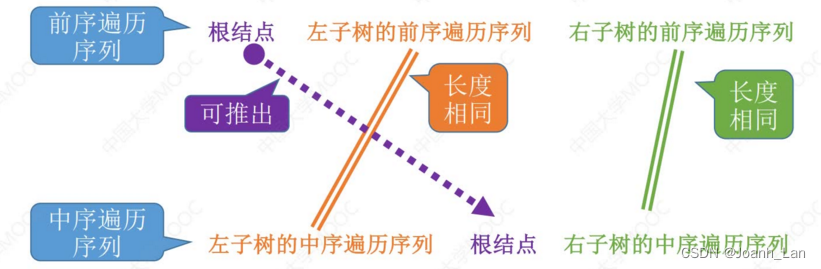
Eg1:
前序遍历序列:A D B C E
中序遍历序列:B D C A E

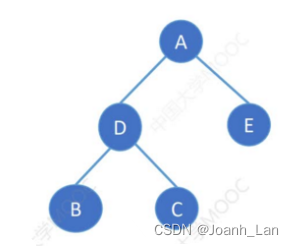
Eg2:
前序遍历序列:D A E F B C H G l
中序遍历序列:E A F D H C B G I

后序＋中序遍历序列

后序遍历:前序遍历$左$子树、前序遍历$右$子树、$根$结点

中序遍历:中序遍历$左$子树、$根$结点、中序遍历$右$子树

Eg:

后序遍历序列:E F A H C I G B D
中序遍历序列:E A F D H C B G l

层序＋中序遍历序列

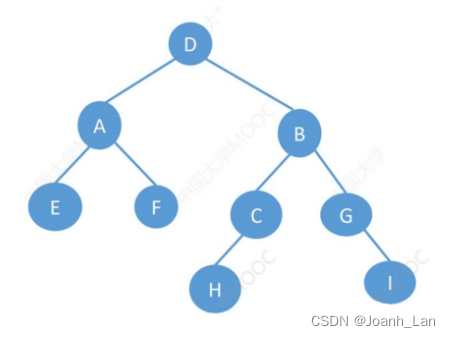
Eg:
层序遍历序列:D A B E F C G H l
中序遍历序列:E A F D H C B G l

若前序、后序、层序序列两两组合?

前序遍历序列:AB
后序遍历序列:BA
层序遍历序列:AB

$结论:前序、后序、层序序列的两两组合无法唯一确定一棵二叉树$

知识点回顾与重要考点

Key:
找到树的根节点，并根据中序序列划分左右子树，再找到左右子树根节点