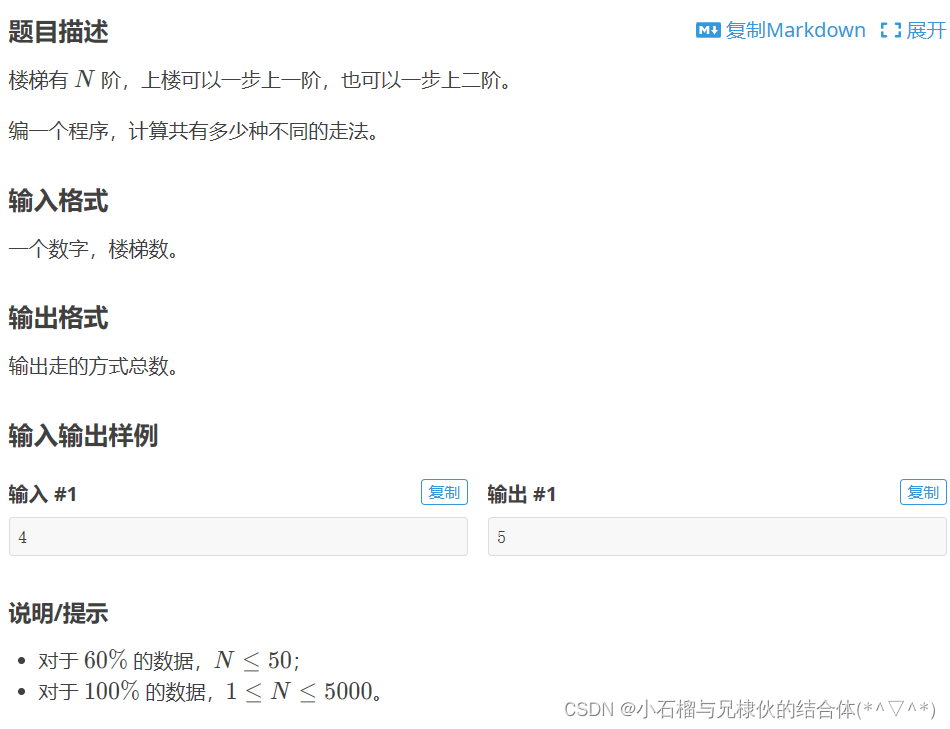
C++ 动态规划 DP教程 (一)思考过程(*/ω\*)
思路:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/156570.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
计算机视觉注意力机制小盘一波 (学习笔记)
将注意力的阶段大改分成了4个阶段
1.将深度神经网络与注意力机制相结合,代表性方法为RAM
⒉.明确预测判别性输入特征,代表性方法为STN
3.隐性且自适应地预测潜在的关键特征,代表方法为SENet
4.自注意力机制
通道注意力
在深度神经网络中…
兴业银行养老金拉新项目上线啦,地推百搭项目
兴业银行养老金就在 ”聚量推客“ 申请开通
今年最火的银行拉新项目就是养老金的 单价高 数据好
目前开通养老金的银行有
兴业银行养老金拉新
交通银行养老金拉新
工商银行养老金拉新
招商银行养老金拉新
浦发银行养老金拉新
广发银行养老金拉新等。。还有很多都开通了…
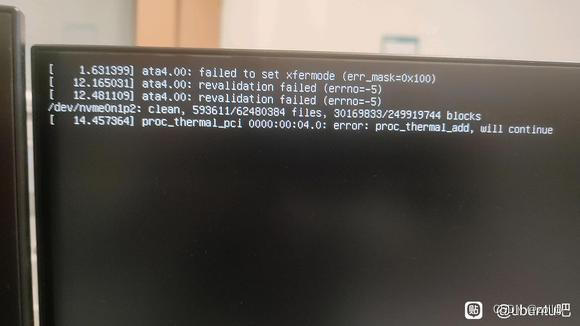
ubuntu启动报错error: proc_thermal_add, will cont
如题,ubuntu启动报错error: proc_thermal_add, will cont
截图如下: 困扰了我很久,差点就打算重装系统,准备放弃了,但是感谢国外的老哥,写了一篇非常详细的解决方案,我搬过来。 解决方案&#…
绝对好用!一个浏览器插件解决跨设备同步问题,吊打文件传输助手!
在数字化的时代,我们所接触的信息呈现指数级的增长。无论是办公资料、学习资源,还是各种生活中的点滴,所有这些信息以各种形式——文本、图片、视频、音乐等——出现在我们面前,如何有效地同步和管理这些内容成为一个挑战。
就跨…
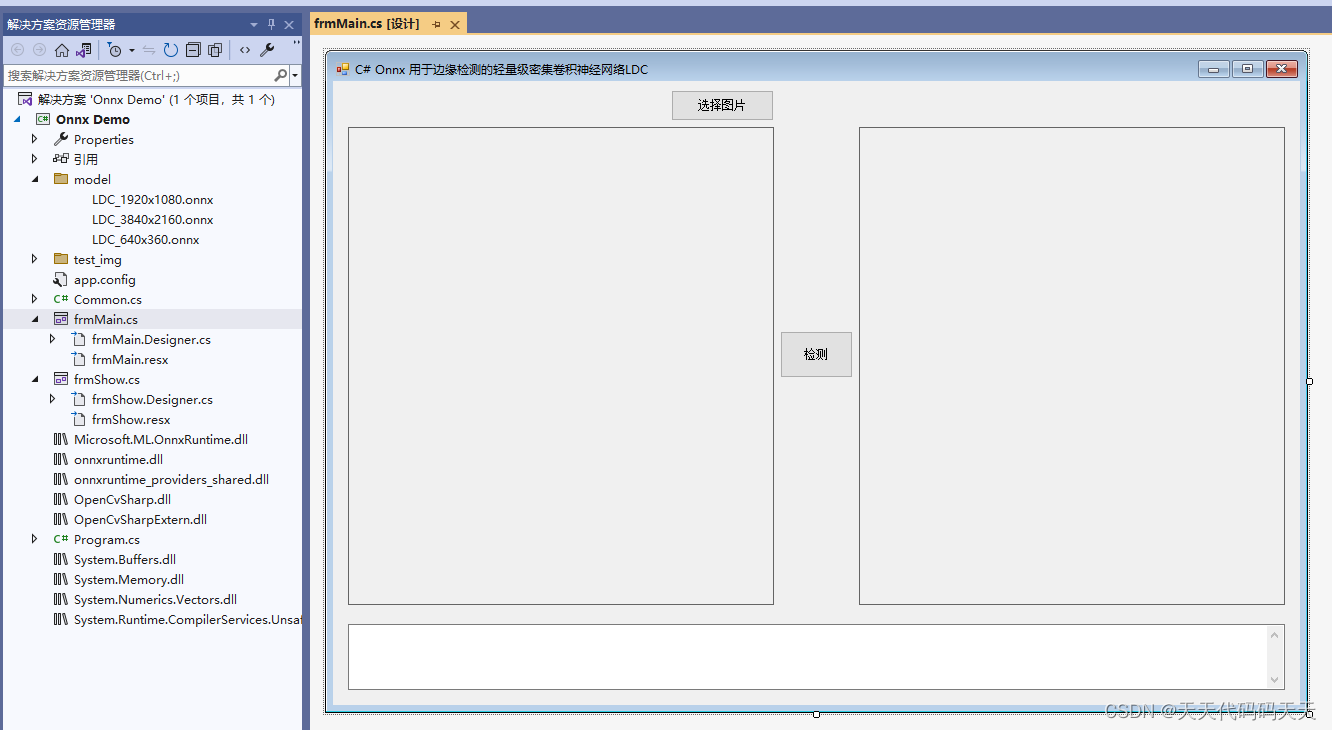
C# Onnx 用于边缘检测的轻量级密集卷积神经网络LDC
效果 项目 代码
using Microsoft.ML.OnnxRuntime;
using Microsoft.ML.OnnxRuntime.Tensors;
using OpenCvSharp;
using System;
using System.Collections.Generic;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;namespace Onnx…
在Java和PostgreSQL枚举之间进行转换的通用方法
枚举类型(enum)是一种方便的数据类型,允许我们指定一个常量列表,对象字段或数据库列可以设置为该列表中的值。
枚举的美妙之处在于我们可以通过提供人类可读格式的枚举常量来确保数据完整性。因此,Java和PostgreSQL原…
5.4 完整性约束命名子句
思维导图: 笔记:5.4 完整性约束命名子句 定义:
完整性约束是在CREATE TABLE语句中定义的。SQL为CREATE TABLE语句提供了CONSTRAINT子句,用于对完整性约束进行命名。命名的目的是方便增加或删除约束。
基本结构:
CONSTRAINT <完整性约束名称> &l…
Flutter的The file name ‘xxxx.dart‘ isn‘t a snake_case identifier警告
文章目录 警告原因分析解决方法dart的一些命名规则变量和函数命名:类和类型命名:常量和枚举:文件命名:包命名:注释:命名一致性:避免缩写:可搜索的命名: 一些好习惯 警告 …
AI“走深向实”,蚂蚁蚁盾在云栖大会发布实体产业「知识交互建模引擎」
数字化起步晚、数据分散稀疏、专业壁垒高、行业知识依赖「老师傅」,是很多传统产业智能化发展面临的难题。2023年云栖大会上,蚂蚁集团安全科技品牌蚁盾发布“知识交互建模引擎”,将实体产业知识与AI模型有机结合,助力企业最快10分…
Redis之 redis.config配置文件
文章目录 前言一、基本配置1.单位2.包含3.网络配置4.通用5.快照6.安全7.限制8.仅追加模式 二、总体主要介绍总结 前言
行家一出手,就知有没有,让一起学习redis.config配置文件。 一、基本配置 Redis 的配置文件位于 Redis 安装目录下,文件名…
表白墙/留言墙 —— 初级SpringBoot项目,练手项目前后端开发(带完整源码) 全方位全步骤手把手教学
🧸欢迎来到dream_ready的博客,📜相信你对这篇博客也感兴趣o (ˉ▽ˉ;) 用户登录前后端开发(一个简单完整的小项目)——SpringBoot与session验证(带前后端源码)全方位全流程超详细教程 目录
项目前端页面展…
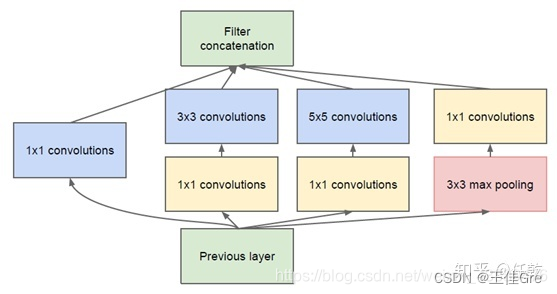
pytorch复现3_GoogLenet
背景: GoogLeNeta是2014年提出的一种全新的深度学习结构,在这之前的AlexNet、VGG等结构都是通过增大网络的深度(层数)来获得更好的训练效果,但层数的增加会带来很多负作用,比如overfit、梯度消失、梯度爆炸等。GoogLeNet通过引入i…