位图介绍

一、位图的引入

先来看下边一道面试题：

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在
这40亿个数中。

经过我们之前的学习，我们可能会有以下的思路：

1. 对这些数进行排序，再通过二分算法，查找这个数是否存在
2. 插入到unordered_set中，使用find函数查找是否存在

上述方法看起来还不错，二分查找算法时间复杂度为logN,而插入到unordered_set中时间复杂度为O(N),而查找时时间复杂度为O(1)，但是都有一个问题就是要将空间不足，40亿个无符号整形，需要160亿字节的空间，大概就是16GB的空间，一般计算机的内促都是4G或者8G，所以空间不足，此时就有了位图的方法来解决：

数据是否在给定的整形数据中，结果是在或者不在，刚好是两种状态，那么可以使用一
个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0
代表不存在。
比如：

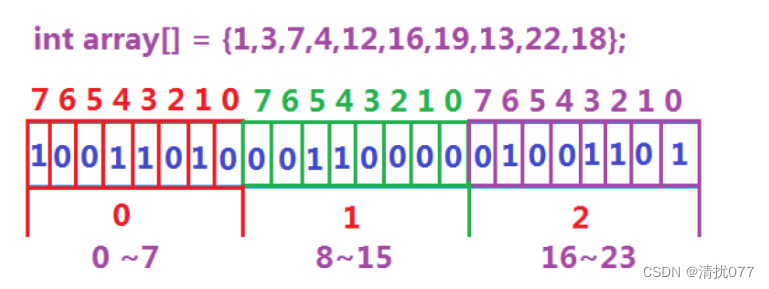
对于上图来说，有一个整形数组，我们可以使用直接定址法对数组的数据进行映射，但是与之前不同的是，此时只是使用一个比特位来代表一个整形数据，当这个数存在时，比特位置1，不存在时，比特位置0,此时就可以大大节省空间资源，无符号整数只有2的32次方个，所以最多开2的32次方个空间，一个空间为一个比特，所以最终只需要512MB的空间。
但是我们不能按照位来空间，最少必须一个字节，所以我们就每次开一个字节的空间，也就是8个比特位，将8位当做一个整体来处理，对要保存的数据除8就是第几个字节，对保存的数据模8就是在这个字节中的第几个位置。

二、位图的概念

所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在的。

那么位图还有哪些应用呢？

1. 快速查找某个数据是否在一个集合中
2. 排序 + 去重
3. 求两个集合的交集、并集等
4. 操作系统中磁盘块标记

位图模拟实现

一、构造函数

由于不能按位开空间，所以我们选择每次开一个字节的空间，由于有范围最大为N，一位关联一个数据，所以需要开N/8个字节的空间，但是有时可能不能整除，所以要开N/8+1个字节的空间。
所以直接在构造函数中开好空间：

		bitset(){_bits.resize(N / 8 + 1,0);}

二、set，reset，test函数

set函数的作用是对位图中的某一位进行填充
i就表示是第几个字节，而j表示该位在该字节中的第几位，所以对1进行左移j位后与该字节按位或，按位或的作用时不论该位为0还是为1，都将该位变为1.

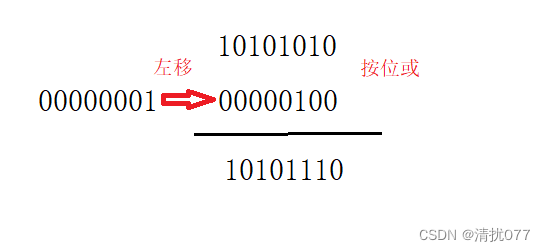
		void set(size_t x){int i = x / 8;int j = x % 8;_bits[i] |= (1 << j);}

reset的作用是将某一位清空
同样的将要清空的那一位置为0，进行按位与，不论原本该位是0还是1，都将该位置0

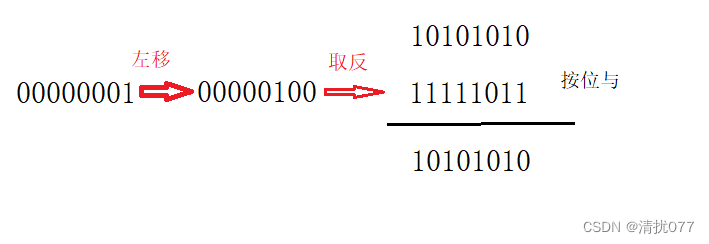
		void reset(size_t x){int i = x / 8;int j = x % 8;_bits[i] &= ~(1 << j);}

test的作用是检测位图中某一位是否存在

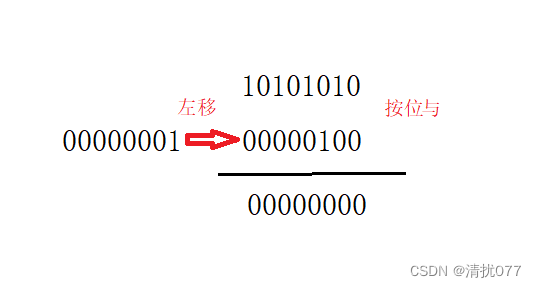
		bool test(size_t x){int i = x / 8;int j = x % 8;return _bits[i] & (1 << j);}

三、代码测试

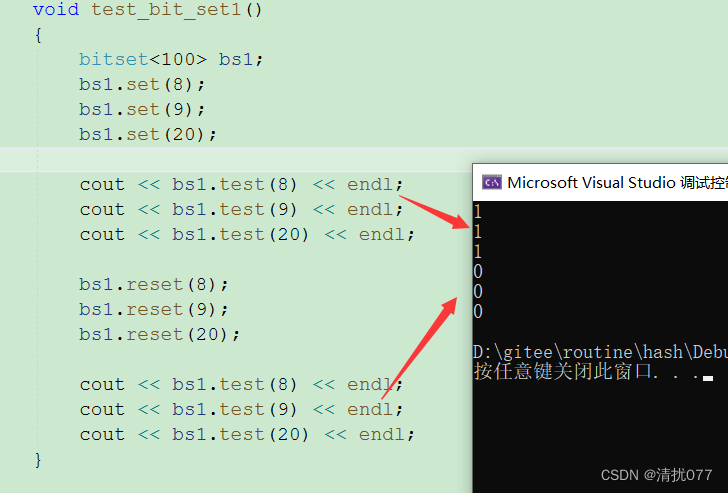
	void test_bit_set1(){bitset<100> bs1;bs1.set(8);bs1.set(9);bs1.set(20);cout << bs1.test(8) << endl;cout << bs1.test(9) << endl;cout << bs1.test(20) << endl;bs1.reset(8);bs1.reset(9);bs1.reset(20);cout << bs1.test(8) << endl;cout << bs1.test(9) << endl;cout << bs1.test(20) << endl;}

四、完整代码

namespace tmt
{template<size_t N>class bitset{public:bitset(){_bits.resize(N / 8 + 1,0);}void set(size_t x){int i = x / 8;int j = x % 8;_bits[i] |= (1 << j);}void reset(size_t x){int i = x / 8;int j = x % 8;_bits[i] &= ~(1 << j);}bool test(size_t x){int i = x / 8;int j = x % 8;return _bits[i] & (1 << j);}private:vector<char> _bits;};void test_bit_set1(){bitset<100> bs1;bs1.set(8);bs1.set(9);bs1.set(20);cout << bs1.test(8) << endl;cout << bs1.test(9) << endl;cout << bs1.test(20) << endl;bs1.reset(8);bs1.reset(9);bs1.reset(20);cout << bs1.test(8) << endl;cout << bs1.test(9) << endl;cout << bs1.test(20) << endl;}