背包问题

说到背包问题大家都会想到使用动规的方式来求解,那么为什么用动规呢,dp数组代表什么呢?初始化是什么,遍历方式又是什么,这篇文章笔者将详细讲解背包问题的经典例题0-1背包问题和完全背包问题的解题方式,希望能帮助到大家
1.暴力方式
有人一提到背包问题就只会使用动态规划来做,那么背包问题假如让你使用暴力求解该如何解决呢?我们以0-1背包为例,每个物品是不是只有两种状态?放或者不放,我们可以遍历所有方式,使用回溯来解决问题.
0-1背包问题解决方式(二维数组)
动规五部曲
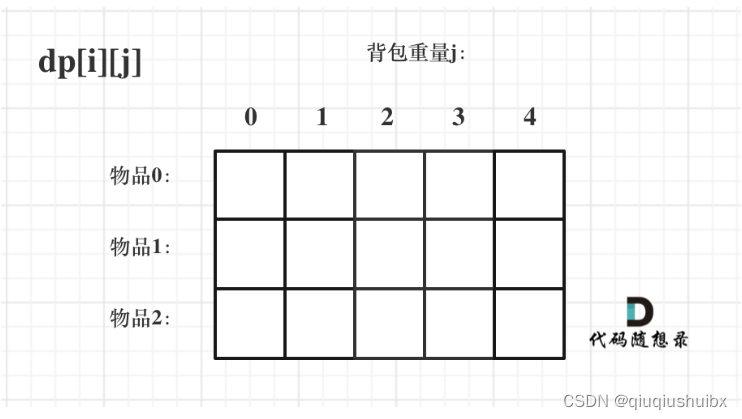
1.明白dp数组的含义
此处dp[i][j]表示的就是从[0,i]个物品中任选,用容量为j的背包能装的最大价值.
2.数组的初始化和递推公式的理解
递推公式:
不放物品:其实就是延续上一层的最大价值即可
dp[i][j] = dp[i-1][j]
放入物品:取上一层的数据或者放入这一层的物品加上剩下的容量的最大价值,两者之间取最大值即可
dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])
初始化数组:
首先从定义出发dp[i][0]一定得初始化为0,0容量的背包装不了东西
由于每一行的数据都是由上一行推导产生的,所以第一行的数据我们也要进行初始化,i从weight[0]开始初始化就行,因为背包的容量的大于等于第一个物品的容量才能装的进去它.
3.遍历顺序的理解
这里我们可以感受一下先遍历背包和先遍历物品的区别,其实都可以达到我们的效果,但是先
遍历物品更好理解
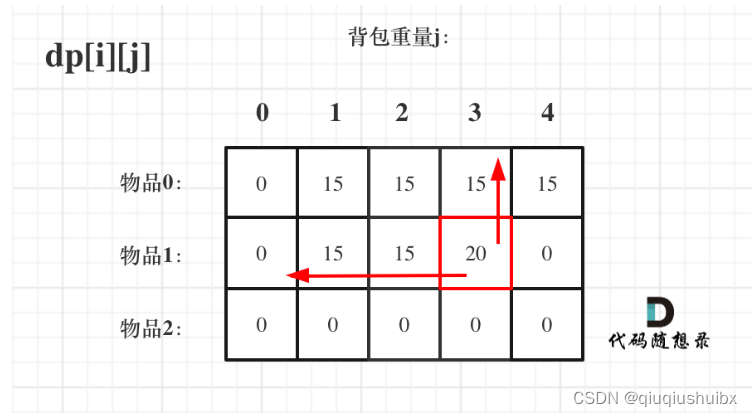
那么为什么两种遍历方式都可以解决问题呢?
如下图所示,因为无论是哪种遍历方式,我们的dp[i][j]都是由左上角的元素推导出来的,所以无所谓用哪种遍历顺序都可以.
for(int i = 1;i<goods;i++){for (int j = 1; j <= bagSize; j++) {if(j<weight[i]){dp[i][j] = dp[i-1][j];}else{dp[i][j] = Math.max(dp[i-1][j],value[i]+dp[i-1][j-weight[i]]);}}}4.打印数组进行查看
0-1背包示例代码
public static void func1(int[] weight, int[] value, int bagSize){//初始化dp数组int goods = weight.length;int[][] dp = new int[goods][bagSize+1];for (int i = weight[0]; i <=bagSize; i++) {dp[0][i] = value[0];}for(int i = 1;i<goods;i++){for (int j = 1; j <= bagSize; j++) {if(j<weight[i]){dp[i][j] = dp[i-1][j];}else{dp[i][j] = Math.max(dp[i-1][j],value[i]+dp[i-1][j-weight[i]]);}}}for (int i = 0; i < goods; i++) {for (int j = 0; j <=bagSize; j++) {System.out.print(dp[i][j]+" ");}System.out.println();}}//main方法中代码int[] value = {15,20,30};int[] weight = {1,3,4};int bagSize = 4;func1(weight,value,bagSize);0-1背包问题解决方式(一维数组)
1.明白dp数组的含义
这里使用一维数组滚动覆盖来代替二维数组,就类似于将一个矩阵压成了一行
我们先回顾一下二维数组的含义dp[i][j]:从[0,i]的物品中,背包容量为j能装的最大价值
这里的dp[j]就是背包容量为j能装的最大价值
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
2.递推公式的理解
我们知道dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
然后递推公式由两个选择,一个是上一层的值和本层的物品价值加上剩余空间价值的较大值
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);3.数组的初始化
根据上面的递推公式,我们知道初始化一定不能初始化成一个大值,因为可能太大了而导致后面的dp[j-weight[i]]+value[i]无法覆盖他的值,所以我们初始化为0即可
4.遍历顺序的理解
我们先上代码,后讲解原因
我们发现这里的背包遍历是从后向前遍历的,为什么呢,举个例子
如果是从前向后遍历
那么dp[1] = dp[1-1]+value[0] = 15
dp[2] = dp[2-1] +value[0]= 30
这不符合我们0-1背包的每件物品只能使用一次的逻辑,因为这里物品1被放入了两次
而我们从后向前遍历就可以避免这个问题
dp[4] = dp[3]+value[0];
dp[3] = dp[2]+value[0];
...这里就不会存在重复计算问题
为什么上面二维数组的遍历不需要倒序呢?
因为二维数组的dp[i][j]是由上一层的元素推导出来,不会影响本层的元素
以为数组的遍历顺序只能是先遍历物品,再遍历背包!!!
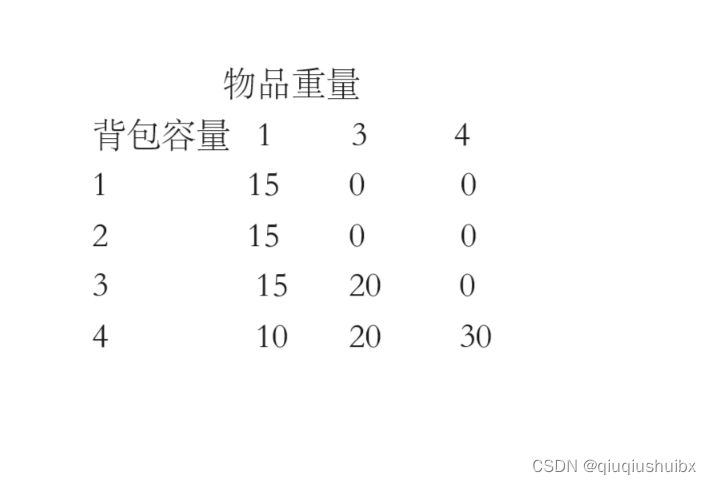
我们还是举个例子来说明(一维数组,我们以二维数组的形式画出来),我们就会发现,如果用容量来遍历物品的话,其实就是每个容量的背包只取得了一个物品,与答案相悖
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);} }5.打印数组进行查看
示例代码
public static void func2(int[] weight, int[] value, int bagWeight) {int wLen = weight.length;//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值int[] dp = new int[bagWeight + 1];//遍历顺序:先遍历物品,再遍历背包容量for (int i = 0; i < wLen; i++) {for (int j = bagWeight; j >= weight[i]; j--) {dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}//打印dp数组for (int j = 0; j <= bagWeight; j++) {System.out.print(dp[j] + " ");}}
}LeetCode T416 等和子集问题
题目链接:416. 分割等和子集 - 力扣(LeetCode)
题目思路:
利用上述思路,这里的背包容量是数组之和的一半,重量和价值数组都等于源数组,上面给出一定的剪枝,假如出现奇数就直接返回false,出现只有一个元素也直接返回false,下面我给出解题代码.
题目代码:
class Solution {public boolean canPartition(int[] nums) {if(nums.length == 1){return false;}int sum = 0;for(int i:nums){sum += i;}if(sum % 2 == 1){return false;}int bagSize = sum/2;int[] dp = new int[bagSize+1];//初始化均为0for(int i = 0;i<nums.length;i++){for(int j = bagSize;j>=nums[i];j--){dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i]);}}if(dp[bagSize] == bagSize){return true;}return false;}
}