
论文解读:王飞龙,曲晨辉
1、问题背景
\qquad 旅行商问题(TSP)是一种众所周知的路径问题。TSP的目标是在图 G = ( V , E ) G=(V,E) G=(V,E)中找一条以场站为起终点的最短路,访问所有客户点 V V V,同时没有子环路。令 E E E表示网络中的弧集合,每条弧的长度通过欧式范数进行计算,如两个节点 p p p和 q q q之间的距离 d p q = ∣ ∣ v p − v q ∣ ∣ 2 d_{pq}=||v^p-v^q||_2 dpq=∣∣vp−vq∣∣2 ,其中 v p v^p vp和 v q v^q vq分别表示节点 p p p和 q q q的坐标向量。
\qquad CETSP是TSP的一种变体形式,相比于TSP,CETSP中的每一个客户点均拥有一个覆盖域(covering region),旅行商不需要访问么一个客户点本身,只需要到达每一个客户点的覆盖域之内即可。在本文中,假设每个客户点的覆盖域是一个圆形,则只要旅行商经过以客户点 i i i为圆心,半径为 r i r_i ri的圆形区域 D i D_i Di,或者至少到达圆形区域 D i D_i Di的边缘之后,就称旅行商已经服务过客户点 i i i。CETSP的正式定义如下:给定一个二维空间中的节点集合 V = { 0 , . . . , n } V=\{0,...,n\} V={0,...,n},每一个节点的坐标为 ( x ‾ i , y ‾ i ) , i ∈ V (\overline{x}_i,\overline{y}_i),i\in V (xi,yi),i∈V,每一个节点 i i i都在其对应的圆形区域 D i D_i Di的圆心, D i D_i Di的半径为 r i r_i ri。假设网络中不存在重复节点,即 ( x ‾ i , y ‾ i ) ≠ ( x ‾ j , y ‾ j ) , i , j ∈ V , i ≠ j (\overline{x}_i,\overline{y}_i)\neq (\overline{x}_j,\overline{y}_j),i,j\in V,i\neq j (xi,yi)=(xj,yj),i,j∈V,i=j。CETSP需要决策旅行商到达每一个节点覆盖域的坐标 ( x i , y i ) ∈ R 2 , i ∈ V (x_i,y_i)\in \mathbb{R}^2, i \in V (xi,yi)∈R2,i∈V(hitting points),和节点的访问顺序 S = ( k 0 , k 1 , . . . , k n ) , k i ∈ V \mathscr{S}=(k_0,k_1,...,k_n),k_i\in V S=(k0,k1,...,kn),ki∈V,从而使得所有hitting points组成的哈密顿环路的距离最短。下图Figure 1展示了二维空间下的CETSP情景示例。
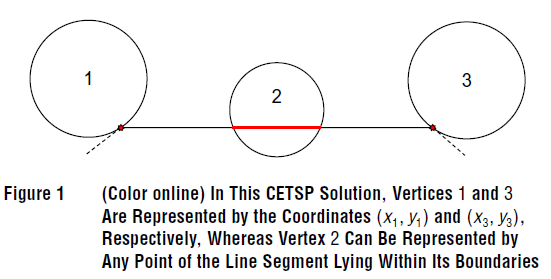
\qquad 其中,节点1和3只被访问了覆盖域中的一个点,节点2的覆盖域和当前路径有一段弧的交集。CETSP可以很简单地拓展到三维空间中去,只需要在每一个节点的坐标中添加一个维度即可,e.g., ( x ‾ i , y ‾ i , z ‾ i ) , i ∈ V (\overline{x}_i,\overline{y}_i,\overline{z}_i),i\in V (xi,yi,zi),i∈V。下图2和3分别展示了CETSP在二维和三维空间中的解方案示意。
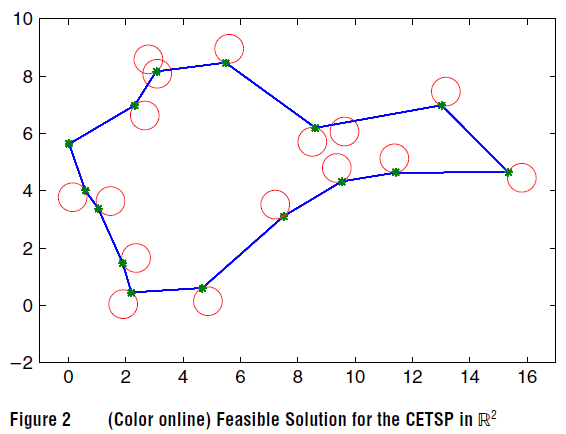
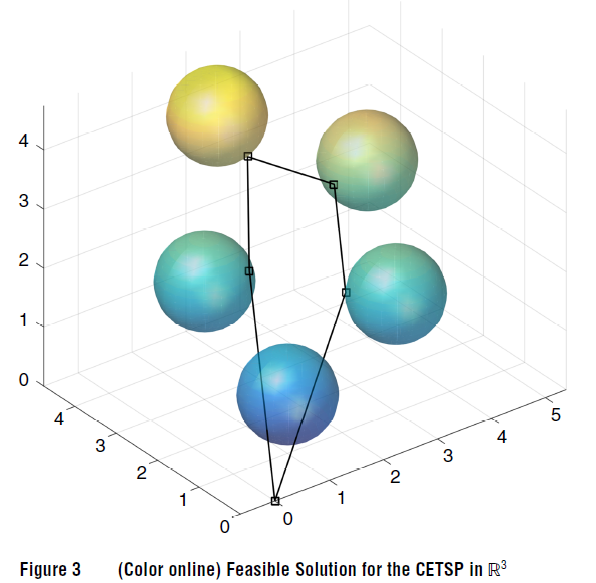
\qquad CETSP在实践中有许多应用场景。如利用射频识别标签来给传输数据。在特定的物理仪表上安装射频标签,之后使用配备有自动抄表系统(AMR)的卡车来远距离收集仪表中的数据,这样卡车不需要访问每一个物理仪表所在的位置,只需要到达距离物理仪表一定的范围即可完成数据的收集和传输工作。近年来,无人机被广泛应用在军事和民用的各个领域。如空中侦查,火灾检测,船舶跟踪,物资配送,地理区域检测,管道检测等。如果为无人机配备无线传感器,其可以远距离对目标进行服务。
\qquad 本文基于分枝定界(branch-and-bound)算法框架设计了一种可以在有限步求解CETSP的精确算法,将CETSP进行分解,子问题是一个二阶锥规划(SOCP),算法可以求解1000个客户点规模的算例到最优,同时通过改变分枝规则和可行性检验规则,算法也可以处理椭圆形状的覆盖域。
2、针对CETSP的分枝定界算法框架
\qquad CETSP的BB框架的整体描述如下:分枝树中每一个节点均表示一个最优的路径片段(partial path),其中只访问了一部分客户点。在根结点,算法随机选择两个客户点作为初始序列的访问客户,同时可知,在TSP问题情境中,由于距离矩阵是对称的,所以只访问两个客户点没有顺序限制,正序和逆序访问的解是等效的。从而可以使用这两个随机选定的客户点组成的序列初始化分枝树的根结点,将这个序列输入到子问题SCOP模型中,得到的解作为原问题的一个有效下界。
\qquad 在分枝的过程中,若所有的客户点均被访问了,并且通过求解子问题得出当前序列是可行的,则找到原问题的一个有效上界,否则需要对分枝树结点进行分枝,随机选择一个未访问的客户点插入到当前序列的每一个位置。当出现下述两种情况时,对分枝树进行剪枝:某个分枝结点的下界解不小于当前最优上界解或者某个分枝结点中的客户点序列中包含所有的客户点。
\qquad 注意到,每一个分枝结点生成的子结点个数为当前分枝结点中包含的结点数量(场站算作一个节点)。下图4展示了包含6个客户点的分枝树示例。
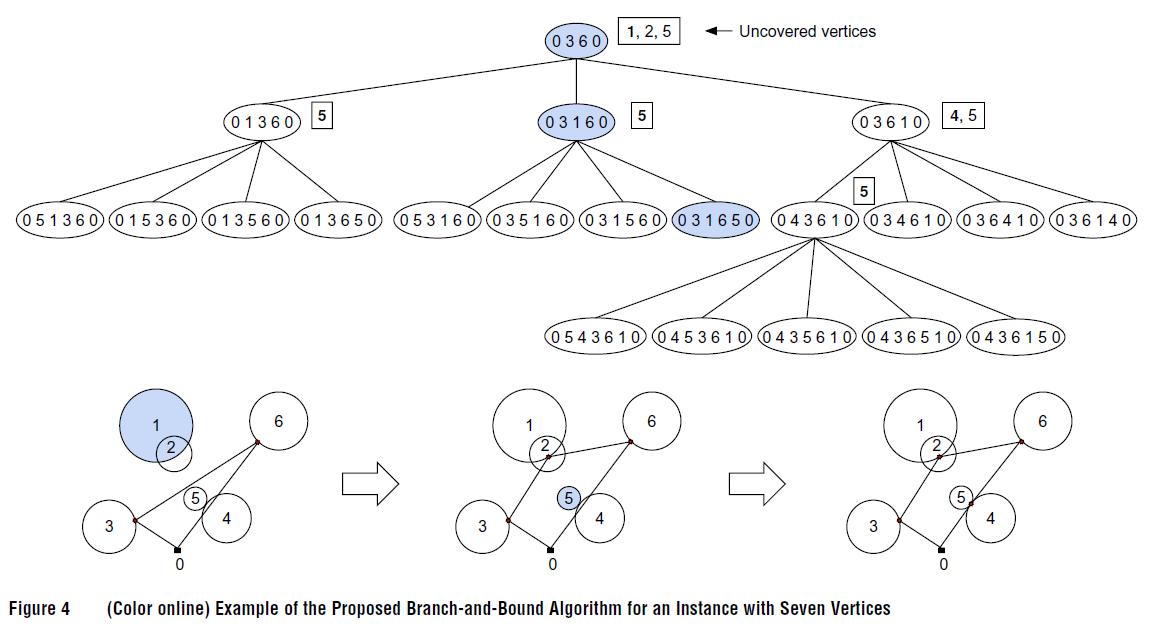
\qquad 上图4中,未被访问的客户点被罗列在每一个分枝结点的右侧方框内,使用加粗表示选定插入的客户点。在这个情境中,根结点的节点序列选定为:0-3-6-0。之后,客户点1被选定插入到0-3-6-0的每一个位置中,生成3个子结点(如图4第二层所示)。当客户1被插入到0-3-6-0的第一个和第二个位置时,客户4可以被顺便访问到,从而0-1-3-6-0和0-3-1-6-0不需要重复访问客户4,但0-3-6-1-0需要对客户4进行访问。之后再对第二层的节点进行分枝,为了简单起见,图中没有罗列出剪枝的情况。最终,得到最优路径为0-3-1-6-5-0。
\qquad 分析分枝树中的节点数量,在分枝树的某一层 l l l最多生成的分枝结点数量为 ( l + 2 ) ! / 2 (l+2)!/2 (l+2)!/2,在最坏情况下,整个分枝过程生成的分枝结点数量为: ∑ l = 0 n ( ( l + 2 ) ! / 2 ) = O ( ( n + 2 ) ! ) \sum_{l=0}^n((l+2)!/2)=\mathscr{O}((n+2)!) ∑l=0n((l+2)!/2)=O((n+2)!)。
2.1 算法描述和精确性分析
\qquad 令 N k \mathcal{N}_k Nk表示第 k k k个分枝树结点,其由一系列节点顺序组成: ( i 0 , . . . , i q ) (i_0,...,i_q) (i0,...,iq), N k \mathcal{N}_k Nk的子问题需要寻找在当前顺序下,访问顺序中每个节点的最优路径。令 c ( N k ) c(\mathcal{N}_k) c(Nk)和 V ( N k ) \mathscr{V}(\mathcal{N}_k) V(Nk)分别表示当前路径的成本和节点集合。
-
若 V ( N k ) = V \mathscr{V}(\mathcal{N}_k)=V V(Nk)=V,则当前节点无需进行后续分枝,被认定为求解完毕,同时使用求解完之后的路径成本更新上界解的值;
-
若 c ( N k ) c(\mathcal{N}_k) c(Nk)不小于当前最优上界,则表明继续对 N k \mathcal{N}_k Nk进行分枝也不能生成更优的解方案,则 N k \mathcal{N}_k Nk被认定为剪枝;
-
否则,选定一个未访问的节点 i ∗ i^* i∗插入到 N k \mathcal{N}_k Nk中并生成 q q q个新的分枝子结点,则 N k \mathcal{N}_k Nk被认定为已处理
\qquad 文中对branch and bound求解CETSP的算法精确性进行了简单证明,应用了反证法的思路,首先令 S \mathscr{S} S 表示最优解方案的序列,令 c ∗ c^* c∗表示最优解目标值,令 N \mathcal{N} N表示一个被剪枝掉的关于 S \mathscr{S} S的一个子序列。根据动态规划的最有性保证,全局最优情况下可以推出局部最优, N \mathcal{N} N作为最优解 S \mathscr{S} S的子序列,存在关系 c ( N ) ≤ c ∗ c(\mathscr{N})\leq c^* c(N)≤c∗成立。若 N \mathcal{N} N被剪枝,则说明有另外一个序列的解方案的值优于 c ∗ c^* c∗,违背了 S \mathscr{S} S为最优解方案的假定,从而 N \mathcal{N} N不会被提前剪枝。
2.2 二阶锥规划
\qquad 为了求解分枝树中每一个结点的子问题,文中提出了一个二阶锥规划模型(SOCP)。令 S = ( i 0 , . . . , i q ) \mathscr{S}=(i_0,...,i_q) S=(i0,...,iq)表示一个分枝树分枝过程中某个分枝结点中的路径序列片段。子问题的的SOCP模型是为了寻找旅行商到达路径序列中每一个节点的位置坐标, ( x i k , y i k ) , k = 0 , . . . , q (x_{i_k},y_{i_k}),k = 0,...,q (xik,yik),k=0,...,q,从而使得路径片段的长度最小化。令 i − 1 = i q i_{-1}=i_q i−1=iq,SOCP的形式如下所示:
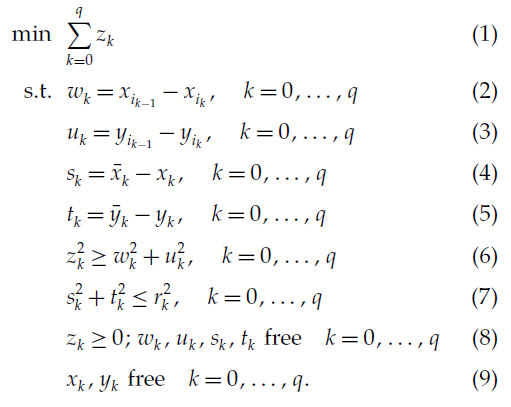
\qquad 在SOCP模型中,目标函数(1)是线性的,变量 z k z_k zk表示旅行商在第 k − 1 k-1 k−1个节点和第 k k k个节点之间行走的欧式距离。变量 w k , u k , s k , t k w_k, u_k, s_k, t_k wk,uk,sk,tk用来表示坐标之间的差值。二阶锥约束(6)表示当前分枝结点中,旅行商在不同节点之间行走的距离约束;二次约束(7)表示旅行商到达每一个节点的位置均需要在当前节点的覆盖域之内。约束(8)和(9)表示变量的取值范围约束。
\qquad SOCP可以再多项式时间内进行有效求解,同时,一些成熟的商用求解器,如CPLEX, Gurobi等都可以用来对SOCP进行有效求解。
2.3 根结点松弛
\qquad 根结点需要选择两个客户点组成初始序列,作为原问题的初始松弛问题。文章采用下述方式进行根结点序列的构建。首先选择场站作为根结点中的第一个节点,之后选择距离场站最近的节点作为第二个节点插入到根结点序列之中。第三个节点的选择需要将剩余没有服务的节点依次插入到根结点序列中,并求解不同序列的SOCP,选择下界值最大的SOCP对应的节点作为根结点的第三个节点。
2.4分枝树结点的可行性检测
\qquad 每一个分枝树结点的可行性检查就是需要检查当前是否所有节点均被服务到了,若是,则称当前分枝树是可行的。可行性检查的关键在于判断当前没有直接访问的客户点的覆盖域是否可以被当前已经构建的路径中的某条弧经过。令 d i ^ \hat{d_i} di^表示当前解方案中距离客户点 i i i最近的弧和客户点 i i i之间的距离,若 d i ^ > r i \hat{d_i}>r_i di^>ri说明客户点 i i i没有被访问到,则将客户点 i i i计入未访问的客户点集合 V ^ = { i ∈ V : d i ^ > r i } \hat{V}=\{i \in V:\hat{d_i}>r_i\} V^={i∈V:di^>ri}。若 V ^ = ∅ \hat{V}=\empty V^=∅,则说明当前结点的解方案已经可行。下面主要介绍对于一个选定的客户点 c c c怎样计算其到某一条弧 p 1 p 2 ‾ \overline{p_1p_2} p1p2的最短距离。客户点 c c c和弧 p 1 p 2 ‾ \overline{p_1p_2} p1p2之间的最短距离可以通过求解 d ^ = m i n 0 ≤ θ ≤ 1 ∣ ∣ ( 1 − θ ) p 1 + θ p 2 − c ∣ ∣ \hat{d}=min_{0 \leq \theta\le 1}||(1-\theta)p_1+\theta p_2-c|| d^=min0≤θ≤1∣∣(1−θ)p1+θp2−c∣∣子优化问题进行求解。其解析解表达形式如下所示:KaTeX parse error: Got function '\rm' with no arguments as superscript at position 22: …^*=-(p_2-p_1)^ \̲r̲m̲{T}(p_1-c)/||p_…,从而最短距离可以通过下式(10)进行计算。
d ^ = { ∣ ∣ p 1 − c ∣ ∣ , i f θ ∗ ≤ 0 ∣ ∣ p − c ∣ ∣ , i f 0 < θ < 1 ∣ ∣ p 2 − c ∣ ∣ , i f θ ≥ 1 \begin{equation} \tag{10} \hat{d}=\left\{ \begin{aligned} %\nonumber &||p_1-c||,\ \ if\ \ \theta^*\le 0\\ &||p-c||,\ \ if\ \ 0<\theta < 1 \\ &||p_2-c||,\ \ if\ \ \theta \ge 1 \\\end{aligned} \right.\end{equation} d^=⎩ ⎨ ⎧∣∣p1−c∣∣, if θ∗≤0∣∣p−c∣∣, if 0<θ<1∣∣p2−c∣∣, if θ≥1(10)
\qquad 其中 p = ( 1 − θ ∗ ) p 1 + θ ∗ p 2 p={(1-\theta^*)p_1+\theta^*p_2} p=(1−θ∗)p1+θ∗p2。假设当前有问题中有 n n n个节点,有 e e e条边,则可行性检查的时间复杂度为: O ( n e ) \mathscr{O}(ne) O(ne),这种检验规则在二维和三维空间之中均适用。
2.5 分枝规则
\qquad 文章基于算例中客户点的覆盖域的半径分布情况,提出了两种分枝方法。所谓的分枝方法就是选择一个未被访问的客户点,将其插入到当前分枝结点对应的序列中。
\qquad 如果所有未被服务的客户点的覆盖域半径均相同,则第一种分枝方法如下执行:首先计算所有未服务的节点中的 d ^ k , k ∈ V ^ \hat{d}_k,k\in \hat{V} d^k,k∈V^,之后选择其中最大的 d ^ k \hat{d}_k d^k对应的客户点作为分枝待插入的客户点,其示意图如下图6所示。
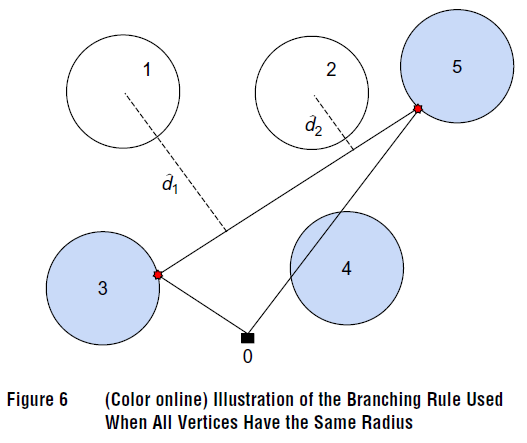
\qquad 这样的分枝规则保证了将节点插入到当前序列之后,下界的增量为 m a x k ∈ V ^ { d ^ k } max_{k\in \hat{V}}\{\hat{d}_k\} maxk∈V^{d^k}的一定比例,但如果所有未被访问的客户点的覆盖域半径不相同,则上述结论也不成立,需要使用下述第二种分枝规则进行分枝。
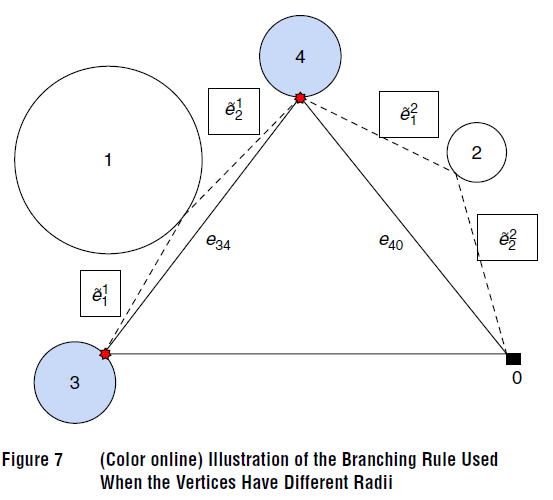
\qquad 对于第二种分枝规则,首先需要估计将某个未被服务的客户点 k ∈ V ^ k\in\hat{V} k∈V^插入到当前序列中后下界增量,记为 r k r_k rk。为了计算 r k r_k rk,首先计算出 D k D_k Dk边界上的一个点 p ~ k \tilde{p}_k p~k,使得 p ~ k \tilde{p}_k p~k到最近的弧 p 1 p 2 ‾ \overline{p_1 p_2} p1p2的距离最短。令 e ~ 1 k \tilde{e}_1^k e~1k和 e ~ 2 k \tilde{e}_2^k e~2k分别表示 p ~ k \tilde{p}_k p~k到 p 1 p_1 p1和 p 2 p_2 p2的距离,令 e i j e_{ij} eij表示弧 p 1 p 2 ‾ \overline{p_1 p_2} p1p2的长度,则 r k = e ~ 1 k + e ~ 2 k − e i j r_k=\tilde{e}_1^k +\tilde{e}_2^k- e_{ij} rk=e~1k+e~2k−eij。计算完所有未访问客户点的 r k r_k rk之后,选定其中最大的 r k r_k rk对应的客户点作为分枝客户点。第二种分枝规则的示意图如下图7所示。
3、计算试验和结果
\qquad 作者进行了一系列的实验,以选择在计算上最有效的分支策略。主要使用了以下策略进行测试:深度优先搜索、广度优先搜索和最佳优先搜索。结果显示,最佳优先搜索是最适合应用于文章算法的策略。所提出的算法在824个实例中进行了测试,这些实例由Mennell(2009)和Behdani和Smith(2014)提出。
3.1 Behdani和Smith(2014)的小实例发现的结果
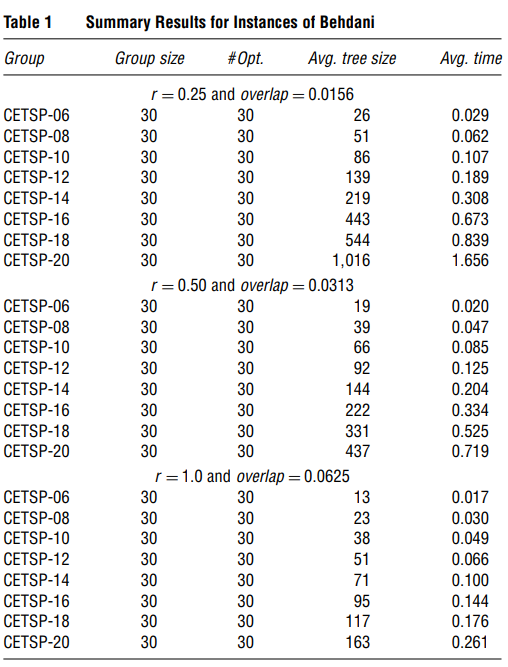
\qquad 表1显示了对Behdani和Smith(2014)的实例所发现的结果的总结。可以看出,所有的实例都在几秒钟内被解决到了最优状态。
3.2 为Mennell(2009)的二维实例找到的结果
\qquad 表2列出了Mennell(2009)的2D实例的结果。每个实例的时间限制为4小时。新的改进(最优)解决方案以黑体字突出显示。通过观察表2的结果,我们可以看到文章提出的B&B算法找到了62个实例中22个的最优解。
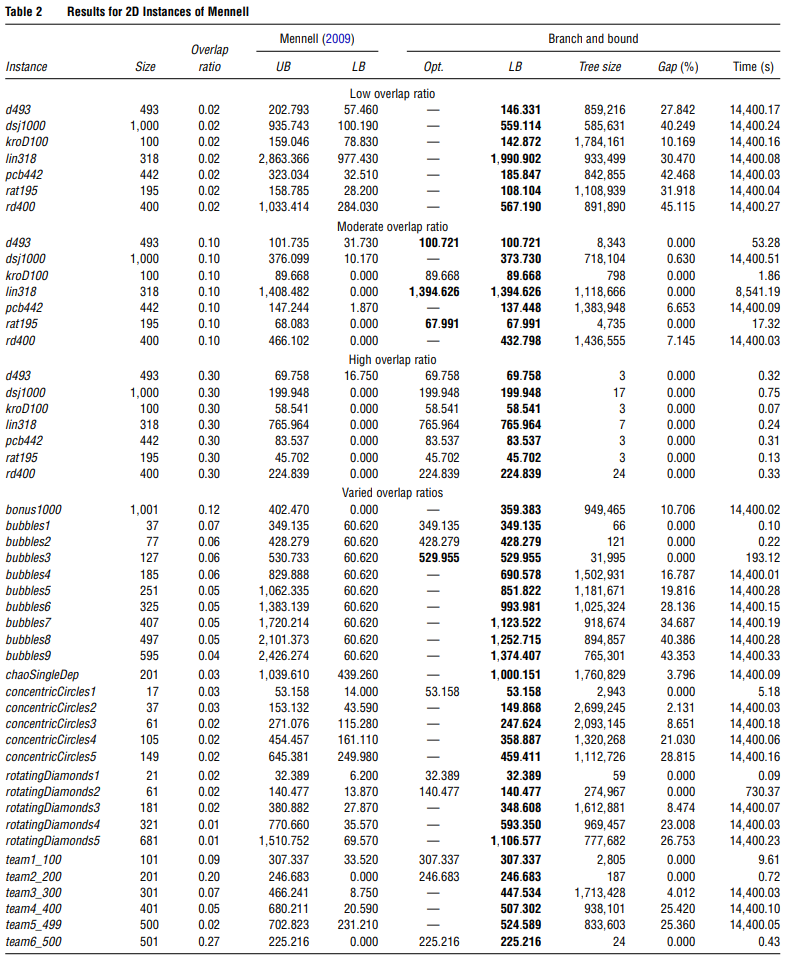
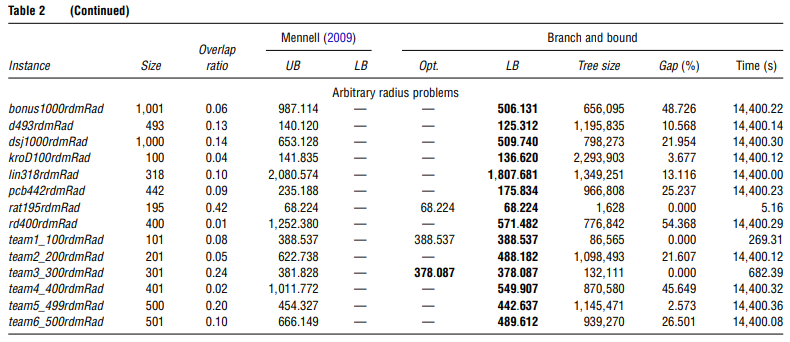
\qquad 我们还可以证实,所有文献中的下限都得到了极大的改善。此外,重叠率越大,算法的效果越好。这在某种程度上是意料之中的,因为最佳旅游路线中的顶点数量往往与重叠率值成反比,从而有助于B&B算法快速收敛到最佳解决方案,因为整个树上需要探索的节点较少。下图8-10描述了部分相关的最优路由。
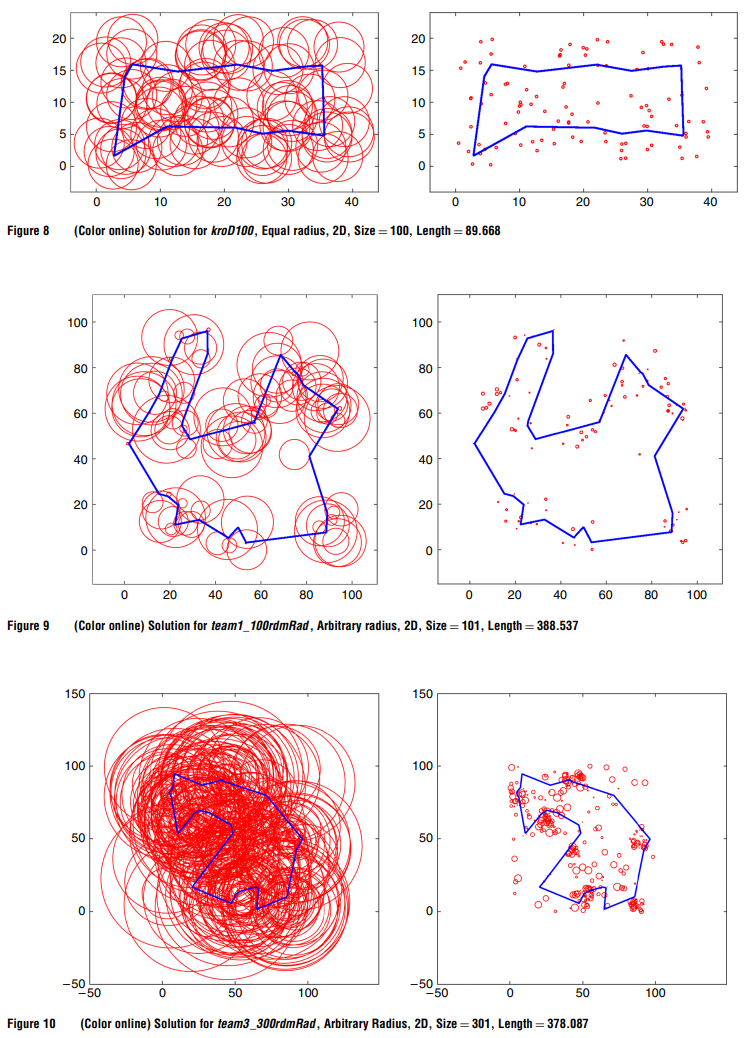
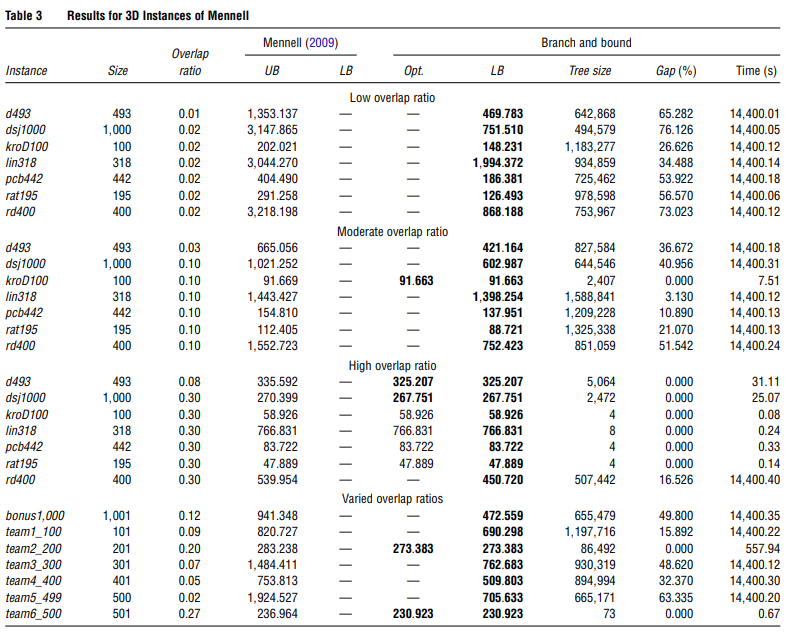
3.3 为Mennell(2009)的三维实例找到的结果
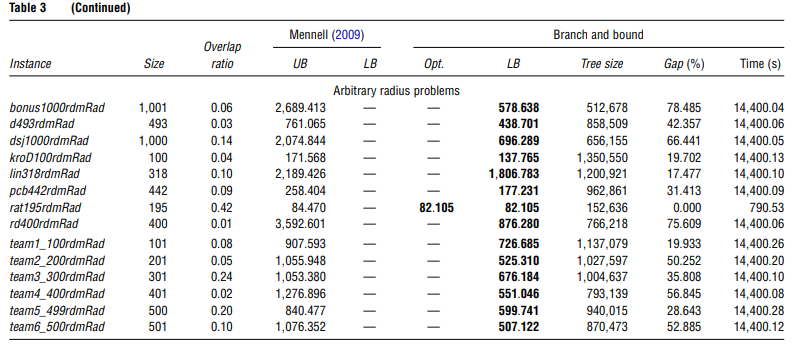
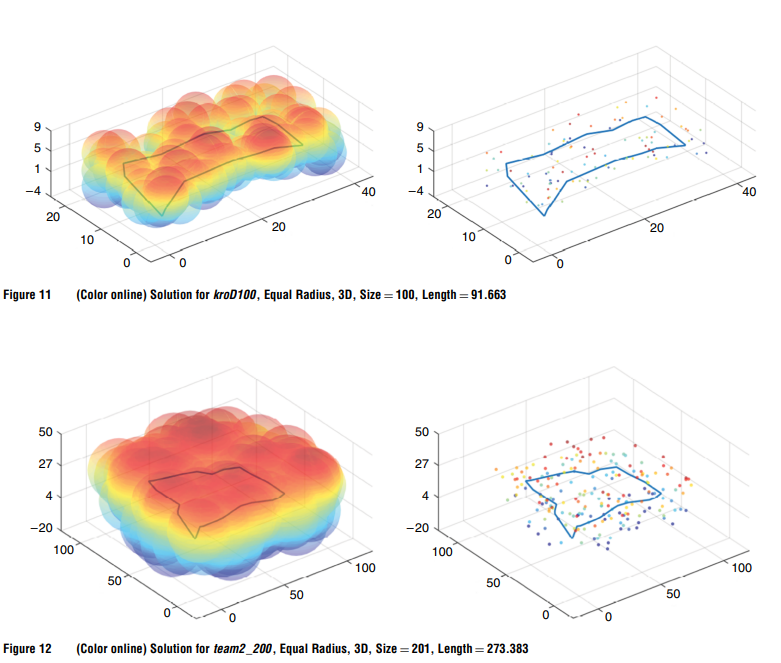
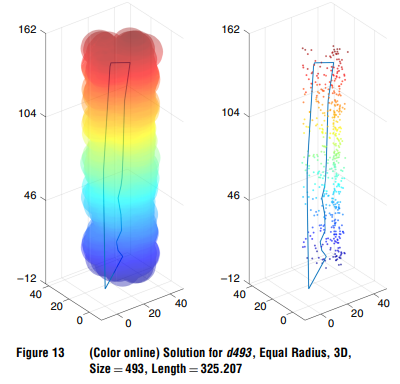
\qquad 表3列出了Mennell(2009)的三维实例所得到的结果。本表中各列的含义与上一节相同。我们的算法找到了42个实例中的10个最优解。此外,所有的下限都得到了改善。图11-13中显示了一些相关的最优路由。
3.4 重叠率对算法性能的影响
\qquad 如前所述,实例的难度与它的重叠率有关。在这一节中,我们提供了一些关于算法在对一个实例采用不同重叠率时的性能的见解。
\qquad 重叠率可以简单地定义为每个顶点的半径和涉及它的矩形的最大边,也就是说, o v e r l a p r a t i o = r / l m a x overlap ratio=r/l_{max} overlapratio=r/lmax,其中 r r r是每个覆盖圆的大小。对于Mennell(2009)建议的名为TSPLIB问题的基准数据集,所有顶点都有相同的半径。因此,我们可以通过将 r r r乘以一个常数 f f f来改变每个实例的重叠率,这里表示为半径因子。
\qquad 鉴于此,我们可以进行一个简单的实验来证明重叠率对分支和边界算法性能的影响。具体来说,我们对上述基准数据集的每个实例都运行了提出的算法,但考虑了 f f f的不同值,范围从0.5到1.5。
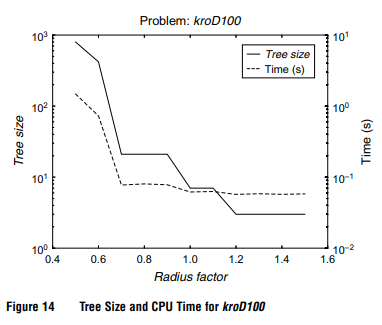
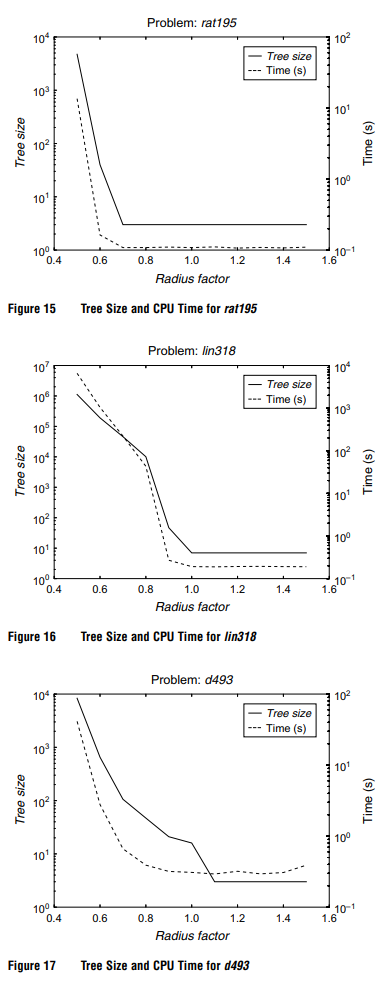
\qquad 正如预期的那样,该算法的性能随着顶点之间重叠度的增加而提高。此外,B&B节点的数量以及计算时间高度依赖于每个实例的重叠率。因此,对于顶点半径非常小的实例,枚举方案在实践中可能会失败。还要注意的是,如果重叠率下降到某一数值,这些性能指标可能会爆炸。一些实例的结果显示在图14-17中,从图中可以看出,以对数尺度,树的大小(连续线)和计算时间(虚线)是如何随着重叠率的增加而减少的。
4、结论和总结
\qquad 文章基于branch and bound算法框架,针对CETSP提出了一种精确求解算法,其中每个分枝结点的子问题都需要求解一个二阶锥规划来计算每一个客户点覆盖域中的最优访问位置。文章对824个benchmark算例进行了测试和计算,得到了其中752个算例的最优解方案,同时对于算例的整体下界有明显的改善。
\qquad 通过算例验证,文中提出的算法对于节点覆盖域重叠较大的算例计算效果较好,对于节点覆盖域重叠较小的算例(更加贴近TSP情景)的算例计算效果较差。从而后续研究可以针对节点覆盖域重叠较小的情景设计更加有效的方法来提升“根结点松弛”策略,加速此类算例的求解速度。
参考文献
Coutinho, W. P., Nascimento, R. Q. D., Pessoa, A. A., & Subramanian, A. (2016). A branch-and-bound algorithm for the close-enough traveling salesman problem. INFORMS Journal on Computing, 28(4), 752-765.





![[CVPR‘23] PanoHead: Geometry-Aware 3D Full-Head Synthesis in 360 deg](https://img-blog.csdnimg.cn/ced3bfe97c004288bb20bf202e078812.png)


