1、数值稳定性
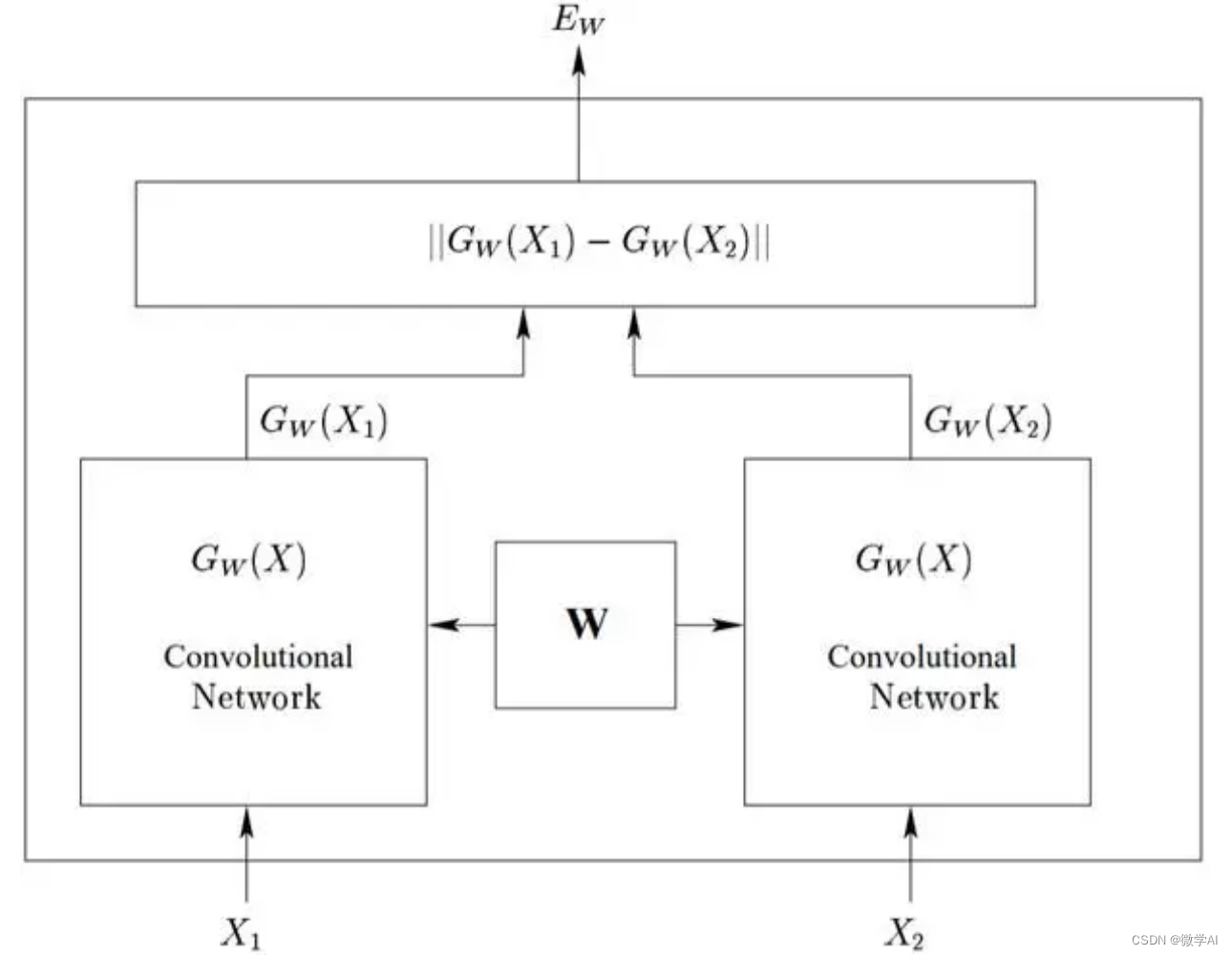
考虑一个具有 L L L层、输入 x \mathbf{x} x和输出 o \mathbf{o} o的深层网络。每一层 l l l由变换 f l f_l fl定义,该变换的参数为权重 W ( l ) \mathbf{W}^{(l)} W(l),其隐藏变量是 h ( l ) \mathbf{h}^{(l)} h(l)(令 h ( 0 ) = x \mathbf{h}^{(0)} = \mathbf{x} h(0)=x)。我们的网络可以表示为:
h ( l ) = f l ( h ( l − 1 ) ) 因此 o = f L ∘ … ∘ f 1 ( x ) . \mathbf{h}^{(l)} = f_l (\mathbf{h}^{(l-1)}) \text{ 因此 } \mathbf{o} = f_L \circ \ldots \circ f_1(\mathbf{x}). h(l)=fl(h(l−1)) 因此 o=fL∘…∘f1(x).
如果所有隐藏变量和输入都是向量,我们可以将 o \mathbf{o} o关于任何一组参数 W ( l ) \mathbf{W}^{(l)} W(l)的梯度写为下式:
∂ W ( l ) o = ∂ h ( L − 1 ) h ( L ) ⏟ M ( L ) = d e f ⋅ … ⋅ ∂ h ( l ) h ( l + 1 ) ⏟ M ( l + 1 ) = d e f ∂ W ( l ) h ( l ) ⏟ v ( l ) = d e f . \partial_{\mathbf{W}^{(l)}} \mathbf{o} = \underbrace{\partial_{\mathbf{h}^{(L-1)}} \mathbf{h}^{(L)}}_{ \mathbf{M}^{(L)} \stackrel{\mathrm{def}}{=}} \cdot \ldots \cdot \underbrace{\partial_{\mathbf{h}^{(l)}} \mathbf{h}^{(l+1)}}_{ \mathbf{M}^{(l+1)} \stackrel{\mathrm{def}}{=}} \underbrace{\partial_{\mathbf{W}^{(l)}} \mathbf{h}^{(l)}}_{ \mathbf{v}^{(l)} \stackrel{\mathrm{def}}{=}}. ∂W(l)o=M(L)=def ∂h(L−1)h(L)⋅…⋅M(l+1)=def ∂h(l)h(l+1)v(l)=def ∂W(l)h(l).
换言之,该梯度是 L − l L-l L−l个矩阵 M ( L ) ⋅ … ⋅ M ( l + 1 ) \mathbf{M}^{(L)} \cdot \ldots \cdot \mathbf{M}^{(l+1)} M(L)⋅…⋅M(l+1)与梯度向量 v ( l ) \mathbf{v}^{(l)} v(l)的乘积。因此,我们容易受到数值下溢问题的影响.当将太多的概率乘在一起时,这些问题经常会出现。 在处理概率时,一个常见的技巧是切换到对数空间,即将数值表示的压力从尾数转移到指数。 不幸的是,上面的问题更为严重:最初,矩阵 M ( l ) \mathbf{M}^{(l)} M(l) 可能具有各种各样的特征值。他们可能很小,也可能很大;他们的乘积可能非常大,也可能非常小。
不稳定梯度带来的风险不止在于数值表示;不稳定梯度也威胁到我们优化算法的稳定性。我们可能面临一些问题。要么是梯度爆炸(gradient exploding)问题:参数更新过大,破坏了模型的稳定收敛;要么是梯度消失(gradient vanishing)问题:参数更新过小,在每次更新时几乎不会移动,导致模型无法学习。
1. 梯度爆炸
当梯度越来越大时,由于链式法则的作用会让这种变化越来越强,梯度会变得更大,最终导致梯度爆炸。

多个数值相乘,越乘越大。

2. 梯度消失
当梯度越来越小时,由于链式法则的作用会让这种变化越来越强,梯度会变得更小,最终导致梯度消失,模型参数不会有过多的更新。
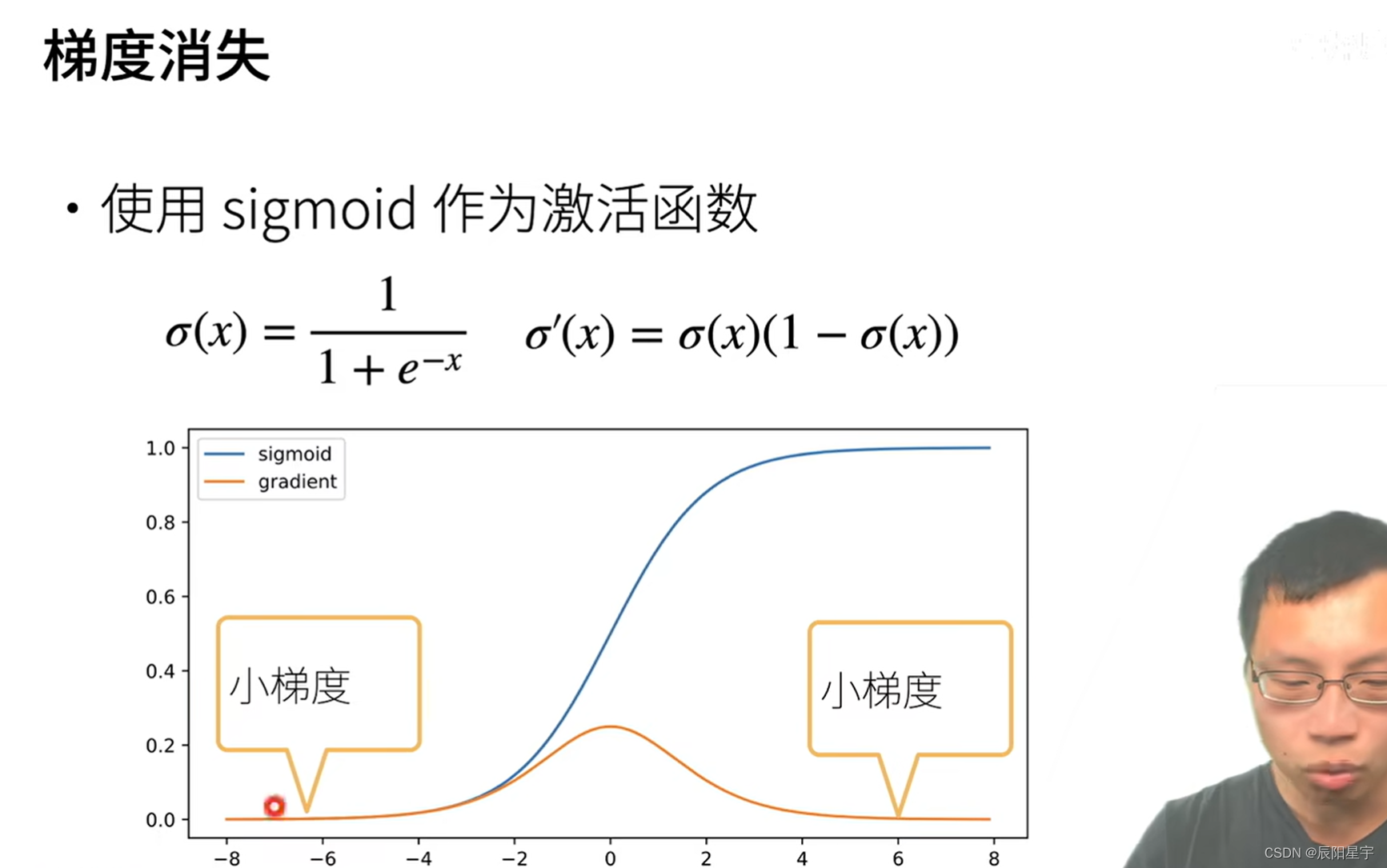
sigmoid的取值范围在(0, 1),两侧区域“饱和”,梯度趋近于0。

多个数值相乘,越乘越小。

3. 解决方法

2、参数初始化

1. 默认初始化
在前面的部分中,例如我们使用正态分布来初始化权重值。如果我们不指定初始化方法, 框架将使用默认的随机初始化方法,对于中等难度的问题,这种方法通常很有效。
2. Xavier初始化
Xavier初始化的一个目的就是使前向传播和反向传播过程中每一层的输入和输出都具有相似的分布,即输入和输出的方差相同。Xavier初始化表明,对于每一层,输出的方差不受输入数量的影响,任何梯度的方差不受输出数量的影响。
Xavier初始化的基本思想是保持输入和输出的方差一致,这样就避免了所有输出值都趋向于0,使得网络中信息可以更好的流动。
参考文章:4.8. 数值稳定性和模型初始化、Xavier初始化、深度学习之参数初始化(一)——Xavier初始化