#pic_center
R 1 R_1 R1
R 2 R^2 R2
目录
- 知识框架
- No.1 线性回归+基础优化算法
- 一、线性回归
- 1、买房案例
- 2、买房模型简化
- 3、线性模型
- 4、神经网络
- 5、损失函数
- 6、训练数据
- 7、参数学习
- 8、显示解
- 9、总结
- 二、 基础优化算法
- 1、梯度下降
- 2、学习率
- 3、小批量随机梯度下降
- 4、批量大小
- 5、总结
- 三、 线性回归的从零开始实现
- 1、D2L注意点
- 四、线性回归的简洁实现
- 五、QA
- No.2 Softmax回归+损失函数+图片分类数据集
- 一、Softmax回归
- 1、Softmax回归
- 2、回归vs分类
- 3、常见分类问题
- 4、从回归到多类分类
- 5、从回归到多类分类―均方损失
- 6、从回归到多类分类―校验比例
- 7、Softmax和交叉嫡损失
- 8、总结
- 二、损失函数
- 1、损失函数
- 2、L2 Loss
- 3、L1 Loss
- 4、Huber
- 三、图片分类数据集
- 四、Softmax回归从零开始
- 五、Softmax回归简单实现
- 六、QA
知识框架
No.1 线性回归+基础优化算法
一、线性回归
- 线性回归是机器学习最基础的一个模型;也是理解之后所有深度学习模型的基础;
1、买房案例
- 这个应用是关于如何在美国购房。与在其他地方购房类似,首先我们需要考察房屋,了解其各种信息。有一点不同之处在于,当我看中一处房产后,如果要购买,我需要进行谈判。例如,这里有一处房产,基本信息显示其售价约为550万美元,拥有7个卧室和5个卫生间,居住面积为4,865平方英尺,相当于约460平方米。但需要注意的是,这个价格并非最终成交价,它只是我的房产经纪人列出的价格。此外,你还可以查看美国一家知名房产网站对这处房产的估价约为540万美元。然而,这两个价格仅供参考,最终你需要提出一个价格。因此,这涉及到一个预测问题,你需要根据当前市场情况来预测能够以多少价格购买这处房产。

- 可以看到,我提供的是标价和预计价格,然后我们需要提出一个报价。在这里,你的报价至关重要,因为这涉及实际的金钱。我们再来看两个房产。
- 然后,你的X轴代表年份,曲线表示根据历史信息和周围房产的系统评估价格。而美元符号表示你在何时以多少钱购买了这个房产。因此,最好的情况是你的购买价格明显低于系统的估值,这意味着你可以获得更好的交易。
- 然而,对于我们来说,作为第一次购房者,我们当时并不了解所有规则,结果多支付了10万美元。所以,一年后,系统对这个房产的评估仍然低于我们的购买价格,造成了约10万美元的差价。因此,从那时起,我们开始关注房价预测这个问题。

2、买房模型简化
- 接下来,我们通过这个应用介绍线性回归。在这里,我们建立了一个简化的模型,基于两个假设。第一个假设是,影响房价的关键因素有三个:卧室数量、卫生间数量和居住面积,我们用X1、X2和X3来表示。虽然还有其他因素,但我们首先考虑一个最简单的模型。第二个假设是,我的成交价格(y)是这些关键因素的加权和,即 y = W1 * X1 + W2 * X2 + W3 * X3 + b。这里的权重W1、W2、W3以及偏差b的实际值将在稍后确定。
- 但在这个假设下,我们假设已经知道这些值,那么我们的成交价格就是这四个项的总和。这构成了我们的核心模型。

3、线性模型
- 现在,让我们将其扩展为一般化的线性模型。给定一个n维输入向量x,其中包括x1到xn这n个分量,我的线性模型将有一个n维权重向量w,包括w1到wn,以及一个标量偏差b。然后,我们的输出将是输入的加权总和,从w1乘以x1一直累加到wn乘以xn,再加上偏差b。如果我们以向量形式表示,这将是输入向量x与权重向量w的内积,再加上标量偏差b。这就是我们的线性模型。

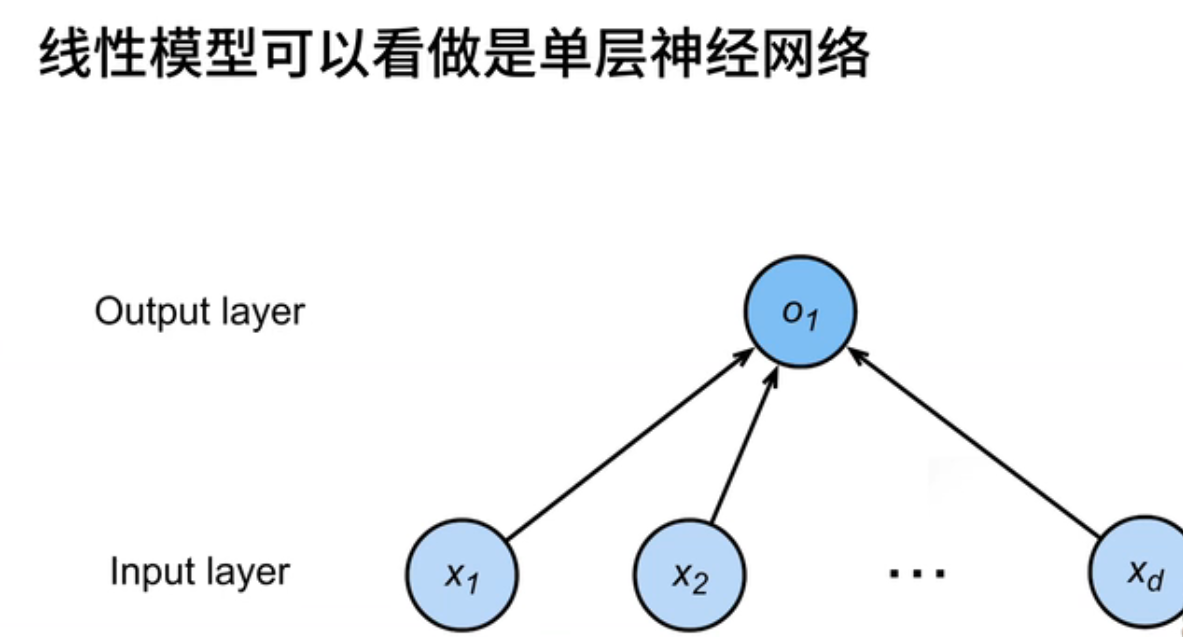
- 线性模型,我们提及它是因为它可以被看作是一个单层神经网络。通常,神经网络被表示为图,包括输入层,这里我们画了n个输入元素,与机器的n匹配。这意味着输入的维度是d,而输出维度为1(O1)。
- 每个箭头代表一个权重。在这里,我们没有绘制偏差。这个神经网络只包括一个输入层和一个输出层,因此它被称为单层神经网络,因为它只有一个带有权重的层。有些人可能不将输出层视为一个独立的层,因为权重和输入层是放在一起的。
4、神经网络
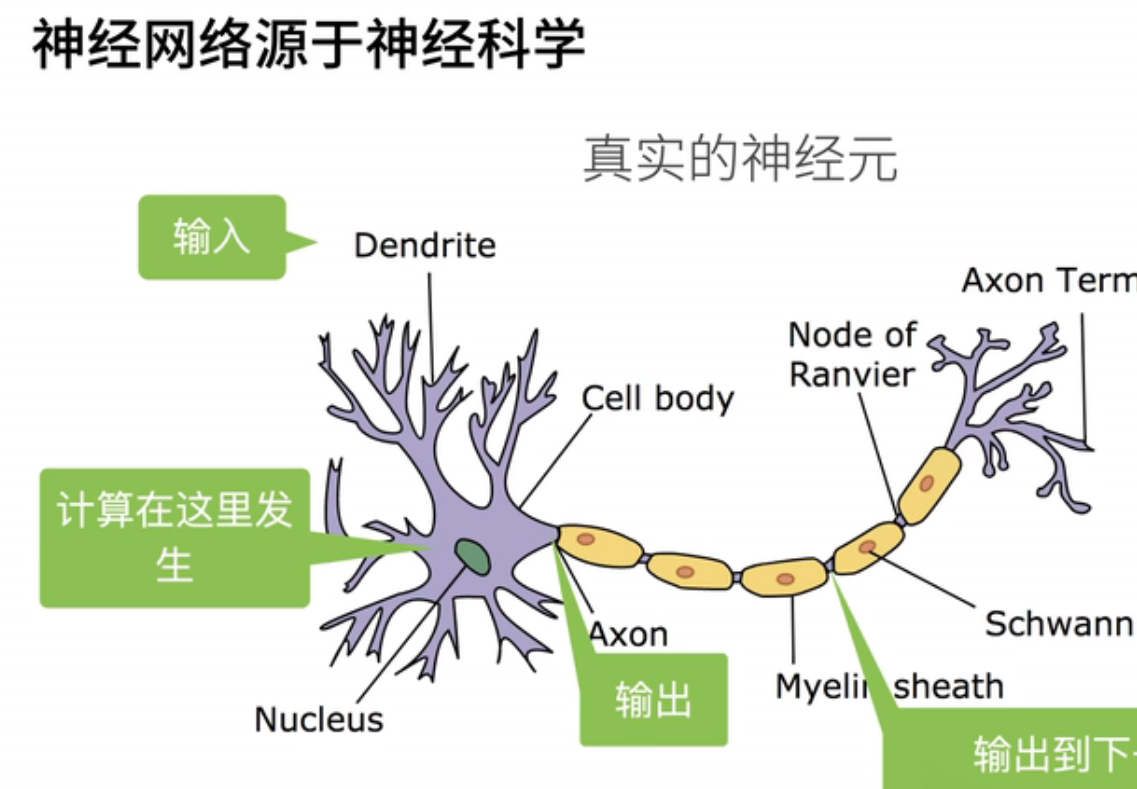
- 第一次提到神经网络是源自神经科学,具体来说是在50年代和60年代。当时,神经科学取得了一些重要突破,激发了人们的兴趣,思考是否能够创建人工神经网络来模拟人类大脑。下面是一个真实神经元的结构。
- 可以看到,神经元的输入相当复杂,然后在神经元内部进行计算。其输出通过连接到下一个神经元,其计算涉及判断输入是否超过阈值。如果超过阈值,神经元会产生神经信号;否则,它将保持不发射。
- 这也解释了为什么我们将这类模型称为神经网络,因为它们灵感来自于神经科学。然而,在过去的几十年中,神经网络的发展已经远远超越了神经科学的范畴,我们不再过于强调这种联系。
5、损失函数
- 我们已经建立了模型,现在可以进行预测。接下来,一个关键的任务是衡量我们的预测质量。具体来说,我们需要比较实际销售价格和预测值之间的差异,也就是我对这个房子的估计。
- 模型的质量与这些差异的大小有关,差异越小,模型质量越高,差异越大,模型质量就越差。因此,我们假设y是真实值,y hat是我们的估计值。一种常见的比较方法是使用平方损失,即1/2乘以真实值减去估计值的平方。这被称为平方损失,因为它衡量了我们未能完全准确预测真实值所导致的损失,或者说经济损失。我们使用1/2的系数是因为在求导时可以方便地消除。

6、训练数据
- 在模型和损失函数确定之后,我们将开始学习参数,即权重和偏差。但如何进行学习呢?我们通过数据来学习。通常,我们首先收集一些数据点来训练我们的模型。例如,在这个例子中,我们可以收集过去六个月内出售的所有房屋的信息以及最终成交价格。这些数据通常被称为训练数据,用于训练我们的模型。一般来说,训练数据越多越好,但实际上,您可能会受到许多限制,例如可用的房屋数量。即使我们收集了所有可用的房屋信息,数据也不会无限多。因此,当数据不足时,我们通常会采用各种技术来处理这个问题,而这将在以后的讨论中详细探讨。现在,让我们先看看训练样本。假设我们有n个样本,我们可以将它们排成一列相量,然后进行转置。因此,我们的大X的每一行对应一个样本,而y同样是一个列向量,其中有n个样本,每个yi都是一个实数值。这就是我们的数据,即x和y。

7、参数学习
- 现在,我们可以着手解决我们的模型了。基于之前的损失函数和给定的数据,我们将评估我们的模型在每个数据点上的损失,并得到一个损失函数。具体来说,我们的损失函数是关于数据x和y以及权重w和偏差b的函数。可以写成如下形式:1/2(这个项来自我们的损失函数) * 1/n(n分之一表示求平均) * 对于每个样本,真实值Yi减去预测值(一个样本的x与权重的累积加偏差)。当然,我们还可以以向量形式表示,即向量y减去矩阵x乘以向量w再减去b(b是一个标量),然后对向量求范数,这就是我们的损失函数。
- 我们的目标是找到一组权重w和偏差b,使得整个损失函数的值最小化。换句话说,我们要最小化损失函数来学习参数。我们选择w和b来表示最小化损失函数的解。这整个过程构成了我们的求解过程。
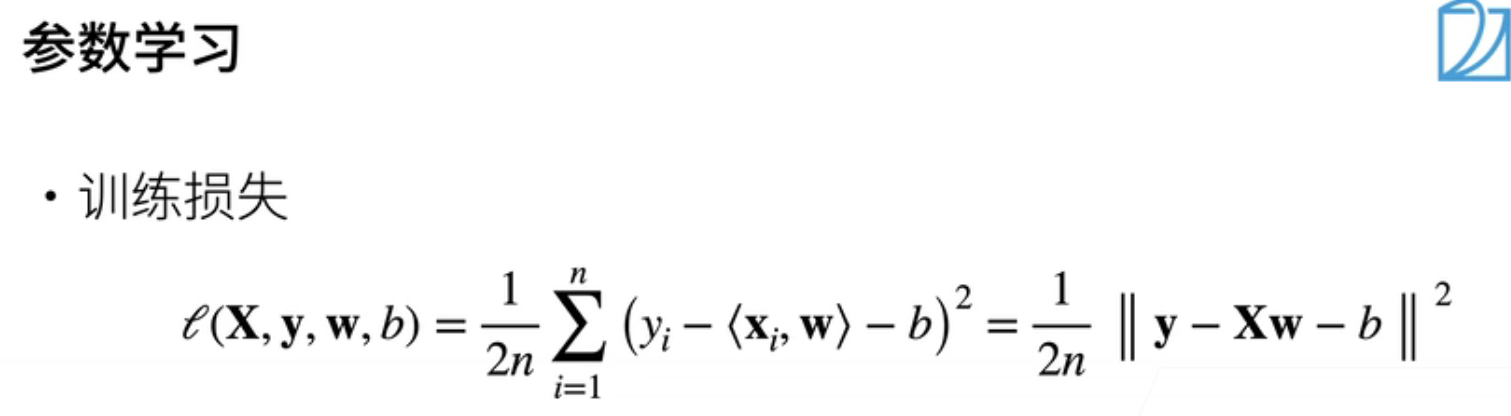

8、显示解
- 线性模型已经讨论完毕,现在让我们来看看它的显式解。最简单的方法是将偏差合并到权重中,以方便书写。具体而言,我们可以在输入特征向量x中添加一列全为1的特征,并将偏差放在权重w的最后一个位置。这样,我们的预测就变成了x乘以w。
- 我们的损失函数可以写成:1/2n * (y减去x乘以w的二范数的平方)。
- 回想一下我们之前介绍的矩阵计算,我们可以对损失函数进行求导。具体而言,我们可以写成:1/2 * (y减去x乘以w)的转置乘以x。由于这是一个线性模型,损失函数是凸函数,虽然我们不会深入解释什么是凸函数,但你可以将其视为一个相对简单的函数。
- 凸函数的性质是其最优解满足使其梯度等于零的点。因此,我们将这个表达式代入,最终得到最优解w*。实际上,它可以计算为x的转置乘以x的逆乘以x的转置乘以y。这是我们最优解的形式。当然,这只适用于线性模型,其他模型将没有这样的显式最优解。
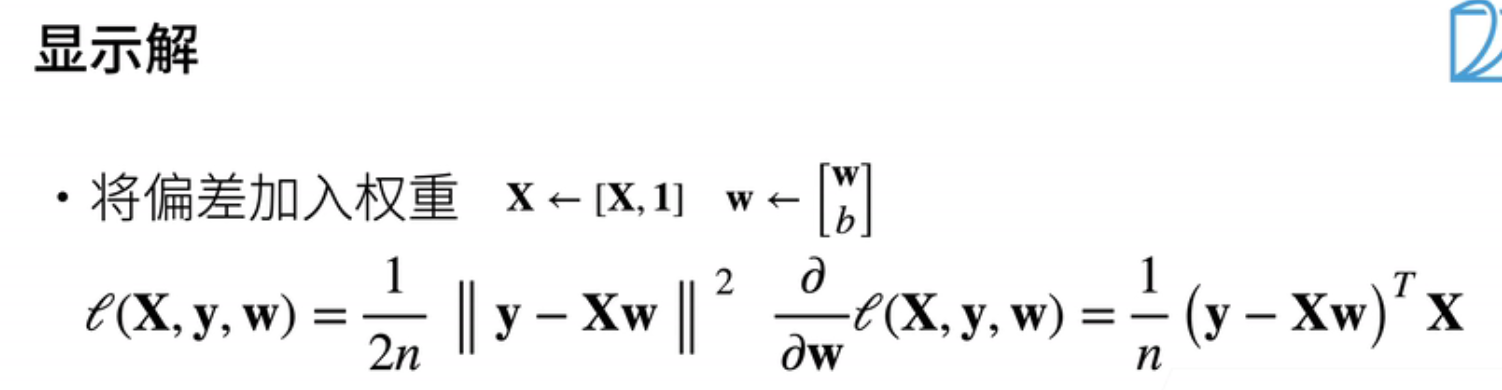
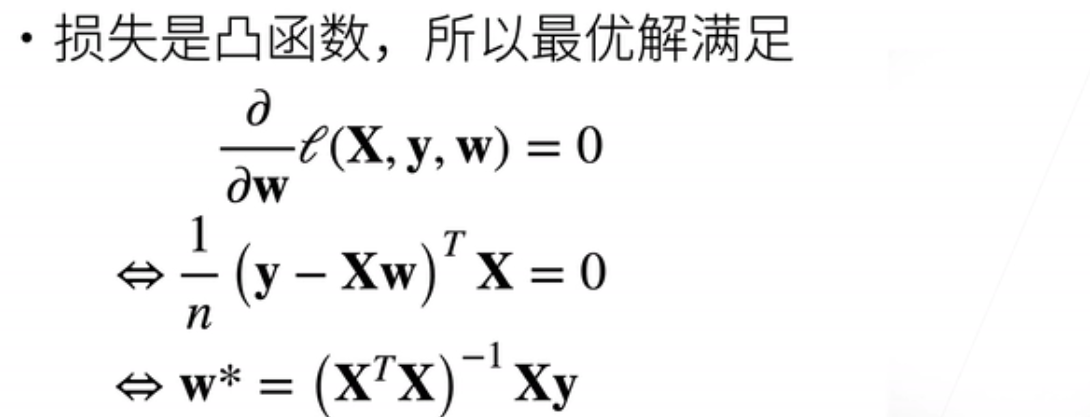
9、总结
- 线性回归是对n维输入的加权和,再加上一个偏差,用于对一个输出值进行估计。通常,它衡量预测值与真实值之间的差异,使用平方损失进行度量。
- 线性回归是一个特殊的模型,具有显式解。需要指出,在这堂课中,其他模型都没有显式解,因为具有显式解的模型通常过于简单。在机器学习中,通常用于解决NP难问题,因此,如果一个模型能够快速求解,它通常有限的能力难以处理复杂的数据和复杂的应用。因此,我们通常不会再追求显式解的模型。
- 最后,我们解释线性回归是因为它确实可以看作是一个单层神经网络,是最简单的神经网络之一。线性回归的介绍到此结束。

二、 基础优化算法
- 在提供线性回归的实现之前;简单的介绍一下优化方法;在接下来会有一大章的内容;来解释各种不一样的优化方法
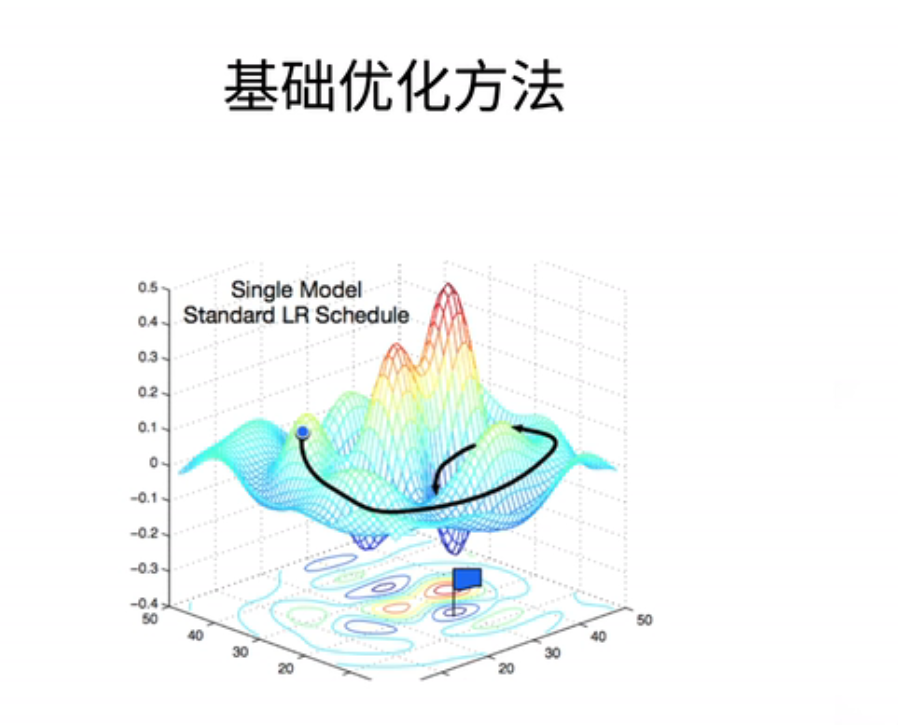
1、梯度下降
- 最常见的算法是梯度下降。当模型没有显式解时,我们可以采用梯度下降来逼近最优解。具体来说,我们首先随机选择一个参数的初始值,可以是任何地方,我们将其记为W0。然后,在接下来的时刻,我们不断更新W0,使其接近最优解。
- 更新的规则如下:WT = W(t-1) - a∇L(W(t-1)),其中∇L(W(t-1))表示在W(t-1)处的梯度,a是学习率。
- 让我们直观解释一下这个过程。下面是一个简单的二次函数的等高图,最优点位于最小值处。如果你看过地图,你可以将每个圈看作函数值等于一个固定值的一条曲线。
- 假设我们的初始值W0位于某处,通常是随机选择的。我们已经解释过梯度指向函数值增加最快的方向,负梯度指向函数值下降最快的方向,就像图中的黄线所示。学习率代表沿着负梯度方向每次前进的距离,比如从一个点走到另一个点之间的向量。通过将W0和这个相邻的向量相加,我们可以得到W1的位置。然后在W1处,我们继续计算梯度,再沿着它前进一步。
- 你可以将这个过程比喻为爬山,你可以选择不走大路,而是每次沿着最陡峭的路径向上爬。这就是梯度下降的直观解释。学习率就是步长,它是一个被称为超参数的值,需要人为指定。


2、学习率
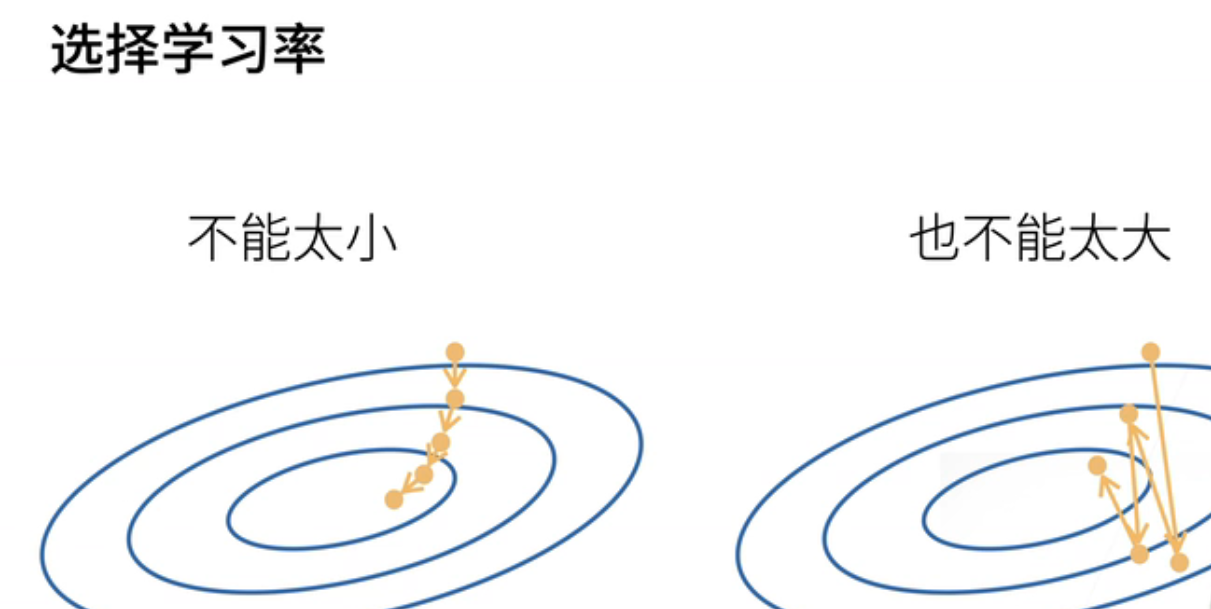
- 首先,我们不能选择太小的学习率。如果学习率太小,每一步前进的距离会非常有限,需要非常多的步骤才能到达目标点。这不是一个好的选择,因为计算梯度是非常昂贵的。我们之前已经提到过,在自动求导中,计算梯度是整个模型训练中最昂贵的部分之一。因此,我们应该尽量减少计算梯度的次数。
- 另一方面,学习率也不能太大。如果步子迈得太大,就有可能跨越了下降的最低点,导致我们一直在震荡而无法真正下降。因此,学习率既不能太小也不能太大。接下来,我们将提供一系列教程,教大家如何选择合适的学习率。
3、小批量随机梯度下降
- 在实际应用中,我们很少直接使用标准梯度下降方法。在深度学习中,最常见的梯度下降变体是小批量随机梯度下降。这是因为在标准梯度下降中,每次计算梯度都需要对整个损失函数进行求导,而这个损失函数是对所有样本的平均损失。
- 这意味着每次求梯度时,我们需要重新计算整个样本集,这是非常昂贵的,可能需要数分钟甚至数小时。通常情况下,我们需要执行数百甚至数千次梯度更新,因此计算成本非常高。为了降低计算成本,我们可以采用近似的方法。我们随机选择一个样本,并使用其损失的平均值来近似整个样本集上的平均损失。这种方法在批量大小(通常用b表示)较大时近似得更精确,但在b较小时近似程度较低。批量大小也是一个重要的超参数。

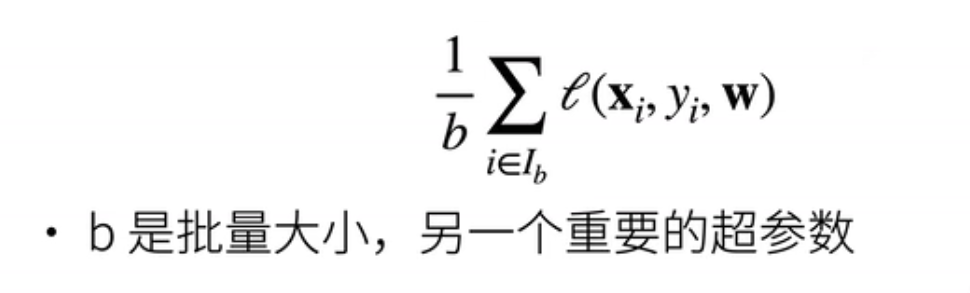
4、批量大小
- 批量大小既不能太大也不能太小。如果批量太小,会导致难以充分利用计算资源。通常,我们会使用GPU进行计算,而GPU通常具有数百甚至上千个核心。当批量太小时,难以充分发挥GPU的计算能力。
- 另一方面,批量太大也会带来问题。批量大小与内存占用通常成正比,特别是在使用GPU时。如果你的GPU内存有限(例如16GB或32GB),那么内存可能成为一个瓶颈,限制了批量大小的选择。
- 此外,如果所有样本都相似或相同,不管批量大小是多少,计算效果都是一样的。这意味着,如果在一个批量中包含大量相似的样本,会浪费计算资源。因此,批量大小的选择应适中,不要太大也不要太小。

5、总结
- 总结一下,梯度下降是一种持续更新模型的方法,通过沿着梯度的反方向来调整模型参数。其主要优点是无需明确知道解的形式,只需要知道如何进行求导。在自动求导章节中,我们讨论了深度学习框架能够自动进行导数计算,因此这一部分变得相对简单。
- 另一个重要的方法是小批量随机梯度下降,它是深度学习中默认的求解方法。尽管有更高级的算法可供选择,但小批量随机梯度下降通常是最稳定和最简单的方法,因此被广泛采用。在这个方法中,有两个关键超参数,即批量大小和学习率。我们将在今后的课程中详细解释如何选择适当的批量大小和学习率。
- 需要注意的是,优化算法是一个庞大的领域,我们将在今后的课程中专门讨论更高级和更稳定的优化算法。然而,对于初步学习而言,了解这个最简单的版本已经足够应对接下来几周的学习。

三、 线性回归的从零开始实现
1、D2L注意点
来实现我们所有;讲过的算法和一些技术细节;这样的好处是说;可以帮助大家从很底层的地方;了解每一个模块;具体是怎么实现的
四、线性回归的简洁实现
五、QA
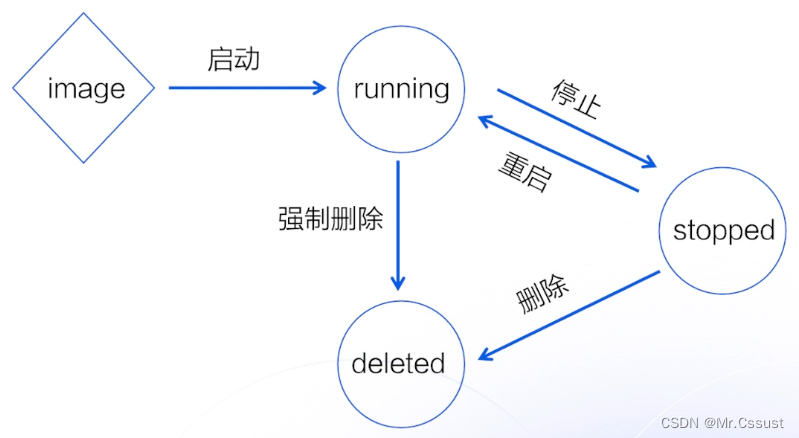
好我们的问题是说;第一个问题是说;请问可以在collab上安装detail;进行环境片;配置吗;可以的;就是说;你在collab上peeping store d tool就行了;就是可以装的;就是你在每一张;理论上在每一张前面我们有个感叹号;peeping store d to l;你是可以可以运行的;或者说;推荐一下对学生党比较便宜的平台;哎;就如果你能够访问Collab的话;我就我就不说怎么访问;哎Collab还是不错的;因为他的话就说比较简单;国内的话我来看一看;我们现在还好;我们现在没有用特别复杂东西;我们这是说之后要用GPU的话;确实会麻烦一点;自己大家不一定要自己去;装一个GPU;这个比较;现在买不到;现在被挖矿的人抢光了;买GP比较难;国内的话;云的话AW有;阿里也有;腾讯应该也有;我我再看一看;好吧就是说;云应该是一个不错的选择;但是用云关键时候不要忘了关机;hello please stop;hello please stop;hello please stop;第二个问题是说;为什么使用平方损失;而不使用绝对差值呢;其实没有太多的;怎么说呢;我们之后会讲一下;平方损失和绝对差值之间的区别;但区别不大;平方损失;最早大家用平方损失是因为绝对差值;它是一个不可不可导的函数;它是一个;当你有;SUB gradient我们之前在;矩阵计算里面应该讲过这个事情;就在 0点的时候;你那个绝对差值;它的导数会有一点点;比较难求;但是说;实际上来说;我们之后会讲一下区别;但实际上没什么太多区别;就是说你用绝对差值;或者用平方损失都问题不大;hello please stop;hello please stop;hello please stop;第三个问题就损失;为什么要求平均;就说你可以不求平均;没关系啦;就是说你求平均和不求平均;本质上没有关系;就说数值是等价的;就是说你求了平均你的梯度;那就是;在一个跟你的一个;就是说在一个样本和的scale上面;你不求平均的话;你的梯度的数值会比较大;那就是说;因为你的除以n在损失上除以n;就等在于我的梯度也除以了n;所以说你;你;如果你反正是用随机提度下降的话;那么你如果不除以n的话;你就把学习率除个n就是了;我给大家演示一下;就说这个值;假设我的l里面没有出个n;那么这一块值;梯度就会变成以前的n倍大小;那么你想得到之前一样的这一块的话;你就把你的学习率除个n就行了;就是你想把n除在这个地方;除在那个地方;基本上没区别;或者是说学习率是怎么学的;使得我的t使得整个这一块不要太大;也不要太小;所以是说除以n的好处是说我;不管你样本;不管你的批量有多大或样本有多大;我的梯度的值都差不多;使得我调学习率的时;候比较好调;就说我不管你的批量大小了;就是比较截偶;但如果你没有除n的话;那你就记得把学习率除了就行了;所以没关系的;;hello please stop;hello please stop;hello please stop;线性回归损失函数是不是通常都是MSC;就是MSC就是我们之前说的那个;是的;一般都是这样子的;hello please stop;hello please stop;hello please stop;关于神经网络;我们是通过误差反馈修改参数;但神经元没有反馈误差这一说;请问这一点是人为推导的吗;这个是一个挺好玩的问题;就是说首先我们提到两件事情;一件事情是说现在其实大家对于;神经网络;对跟人的神经没什么太多区别;第二个事情就是说;确实误差反传;是跟神经元有一定的关系;在神经元里面;大家可以去搜一个叫做赫本的;这个赫赫本的一个一个定律;就是说;他其实是说;神经元还是根会根据你的复反馈;进行一些;预知的调整;就是说他的调整是通过化学元素;神经元放电不放电的调整;他是有一定点的关系;我们之后会讲到一个模型;会叫做感知激;它其实是来自于神经网络的一个;我给大家讲一下它来自神经网络;它本质上等价的是一个提速下降;我们在下一节会讲到;hello please stop;hello please stop;hello please stop;物理实验中;通常使用n减1T的n求误差;请问这里求误差也能n减1T的;n吗就你用谁都没关系;就是说对损失来话;你你需要最小化损失;我不我不关心损失值是多少;我只要最小化;所以跟之前提到的一样;你出个谁都没关系;就是说最后你去学习率调一调就行了;hello please stop hello;please stop hello please stop;第七个问题是说;不管是剃度下降还是随机剃度下降;怎么找到合适的学习率;有什么好办法吗;有两个办法;第一个是说;你找到一个;对学习率不那么敏感的算法;比如说我们就会讲;Adam这种比较smooth的;一些基础下降;就说对学习率不那么下降;敏感第二第二个是说;你可以通过合理的参数的初始化;使得你整个学习率就是个0.1或者0.1;就差不多了;就说你开始不要;我们之后会讲数值稳定性;会给大家解释一下;然后呢还有一个办法是说;有有有这样子的找学习率的方法好;我们可能我们课程;这一次没有安排讲这个事情;我大概想办法在我们的;优化算法那一节;插进来给大家说;怎么样去调一个叫很快的方法;找到一个还合适的一个区间;我们想办法;大家如果我忘了的话;记记得提醒一下我;hello please stop;hello please stop;hello please stop;so bite size是否会影响最终模型的结果;其实你过小是好的;大了不行;就是说可能反直觉;就我们之后可能会讲到;丢弃法就drop power的时候;就是说你的bitch size;小其实对你在同样的计算;就是说我扫数据扫10遍的情况下;bitch size越小;其实是对收敛越好;为什么是因为随机梯度下降;理论上是说给你带来了噪音;就是我每一次他其实在;因为你采样的样本越小;你的噪音越多;因为我有100万个样本;每次采样两张图片;两个样本的话那么噪音就比较大;就跟真实的方向肯定差很远;但是这个噪音对神经网络是哼;是件好事情;因为神经网络;现在深度神经网络都太复杂了;一定的噪音使得你不会走偏;就是说大家说你教小孩的时候;不要一直夸他;对吧你也笑;你也是嗯嗯;操一点;其实对小孩不见得是件坏事情;就是更更;所谓的更鲁棒;就是说对于各种噪音你的容忍度越好;你可能你整个模型的泛化性更好;好我们还没讲泛化性;hello please stop;hello please stop;hello please stop;在过礼盒和嵌礼盒的情况下;学习率和批次应该怎么调整;理论上来说;学习率和批量大小;理论上;是不会影响到最后的一个收敛结果;但是说实际上;因为我们不能完全纠结;所以有一定的影响;但是你会想像是说没那么影响;我们之前所说到;PDM大小太大会导致收敛有问题;但是只要你不是特别特别大;一般来说就是说你就多花点时间;最后还是能收敛的;当然会我们会;可能会在实际上给大家演示一下;如果你真的特别特别大;那就是比较难了;hello please stop;hello please stop;hello please stop;针对批量大小的数据;及进行网络训练的时候;网络中每个参数更新减去的梯度;是bad size中每个样本对应参度的求和;取得平均值吗;是的;就是说理论;它其实的工作原理;因为梯度你知道是个线性;就是说我的损失函数是一个;每个样本相加;去等待是每个样本求梯度;然后去均值;就是说它是个线性关系;是可以写的;;hello please stop;hello please stop;hello please stop;随机梯度下降的随机;是指批量大小是随机的吗;不是;批量大小是一样的;就说我批量大小等于128;那么就是我们之后实现会讲;就说每次我随机的在样本里面采样;128个元素;这就随机的意;随机采样的意思;所以这是为什么;我们要讲讲实现;实现会有所有细节都会给给大家讲;在深度学习中;hello please stop;hello please stop;hello please stop;设置损失函数的时候需要考虑;正则吗;需要的正则;但是我们一般不放在损失函;怎么说呢;我们把损失函数就是那个l two的那个;损失函数;和正则是分开的;我们就会讲到正则项;会需要这个东西;但是也也没有太多用;就说;我们还有很多很多别的方法来做正则;;hello please stop;hello please stop;hello please stop;为什么机器学习的优化算法;都采用梯度下降一阶导算法;而不用流顿法二阶导;收敛更快;一般能算出一阶导二阶导;也能算;首先呢这句话不一定是对的;二阶导不好算;很难算;就是说嗯;不是总是能算出来的;都算起来特别贵;就说你一阶倒是个项量;二阶倒是一个梯度;你要想一想;这梯度是;假设你的纬度是100的话;他的;一阶梯度是一个100的向量;它的二阶梯度就是100*100的矩阵;当你很大的时候;当然就很大了;有很多算法可以做近似;是可以做的;但是真正流动法是做不了的;我们可以做一点近似的流动法;第二个是说;为什么不用流动法;就是说;这个;这个会涉及到比较大的一个话题;我不行不知道要不要特别展开;就是说首先大家要理解的是说;这里面有两个模型;一个是我的统计模型;就是我的损失函数长什么样子;一个是我的优化模小;就是我用什么样算法来求解;这两个东西其实都是错的;比如说我的模型;我的统计模型是错的;我优化模型也不会求到最终解;我们当然现在是可以求最终最优解;但是对于一般来积极函数;积极学习的函数;是求不到最优解的;所以说两个东西都是错的;所以说;所以说;我要把一个统计模型的最优解求出来;意义并不大;因为它是一个错误的模型;你求到最优解;或者不求到最优解的;无所谓;这是第一点;所以是说;你收敛快不快;其实我真的不那么关心;第二点是说;我关心的是说;你收敛到哪一个地方;我们之后会讲到;是说你的真实的损函数;是一个非常非常复杂的;一个一个平面;一个一个曲面;你通过你是牛顿法说我收敛很快;但是你可能找到那个点是一个自由解;不是一个自由解;那个点比较不平坦;所以是说你不见得就算你收敛快;你很快就能得了解;不见得;你最后你的训练出来的模型的泛化性;比我用随机提督下一项找的好;人生也是这样;感慨一下;就是说你不要每次步子迈太快;没必要就是说你;你20岁走上人生巅峰;巅峰so what;你你小步小步走;每次往前走一点;50岁到人生巅峰说不定还高一点呢;对吧;所以是说这个是玄学;我们可以;之后再来看;所以一般说我们;虽然二阶梯度;二阶导算法;在学术上确实最近一些年有很多工作;但是他还没有到像一阶法;那么实用的一个阶段;计算比较复杂;第一点第二点是说收敛不一定快;那就算快;结果不一定好;所以是说大家;在你有那么多的不好的情况下;大家先选最简单的;hello please stop;hello please stop;hello please stop;;学习率怎么除以n;设置学习率的时候吗;是的就是说假设n等于百的话;假设我的损失函数没有除以n;我的学习率等于0.1;那么呢如果你没有;如果你损失函数没有除以n的好;我就把那个0.1除以n嘛;就是除以100嘛;我们最后会可以给大家解释一下;对低态起是干嘛;hello please stop;hello please stop hello please stop;刚看我们最早有个低态函数;就是说告诉你说;我们就不要再不要算梯度了;就是说;就是因为;你可以认为就是说我要传到long派去;我就不要去参加自动求剃度这个事情;就是说;从剃度那个计算图里面给拿出来;就Detouch和和Pistouch的Detouch用法是一样;这个就是Pastouch的Detouch了;就是说;就是说你可以看一下;就是说这个取决Pistouch版本;有些版本新的版本好像是不需要了;就旧版本你需要Detouch一下;就说你到转到pass前要看看这个事情;hello please stop hello please stop hello please stop;接下来的;跟这一节相关的问题;就是说;这样的data iterate的写法;每次把所有的漏的进来;如果数据多的话;最后的内存会爆掉;有没有好办法嘛;是的;这样的内存会爆掉;就是说;如果你的数据特别大的话;假设你数据要100个GB的话;那你的数据就你这样子;就要先note进内存;肯定是不对的;但是我们在整本书;整本书我们用到data set都不会很大;就是就几百兆的样子吧;几百兆东西;写进内存其实问题不大了;其实你真的要在实际情况中;你的比如说你;你真实的有GPU的机器的话;你内存可能其实g也是有的;所以你你就一个10G;20G的数据;你漏的进去也问题不大;所以你不要太担心这个问题;但一般的做法是说因;为我们是真的;就告诉你说从头实现怎么样子;但实际情况中;你是数据是放在硬盘上的;每一次读;就说;比如说我有100万张图片放在硬盘上;每一次;我去随机去把那个图片给抓出来;我是不需要;去真的去把整个数据切漏的进内存;我每一次我只要读到批量大小;和数据进内存就行了;但如果说性能有问题的话;我会往前读几个;批量大小;就说假设我的批量大小是128的话;我读一个再读一个;每次往前读三个;早一点开始读叫就是豫曲prefect;这里的音;hello please stop;hello please stop;hello please stop;this要转成pen;pencil只需要列表不行吗;你可以试一下;应该是不行的;你可以试一下;每每次都随机取出一部分;最后保证所有数据都被拿过了;我们这个实现;是会保证所有数据被拿过了;就说你看到;是说我们把零一直到最后一个的;所有的index全部生成出来;然后render你shift一下;然后一次读;每次读的话;我能保证每扫一次数据;把所有的数据都拿过一次;但是另外有一些;另外一个实践是说我可以不要这么做;每次真的去随机采样一些数据;也是可以的;所以说其实你只要数据;你叠带次数够多的话;你总会拿看到所有的数据;而且你真的你有100万个数据的话;比如举个例子;少看一些数据没关系;其实没什么关系;hello please stop;hello please stop;hello please stop;这里;使用生成器生成数据有什么优势;相对于ten呃;好处是说你生成数据说每一次;就是说;这点好处是说你;比如item的好处是;我不需要把所有的bitch全部生成好;每次我要一个bitch;我就去run一遍;这个是第一个好处;第二个好处就是写起来比较好;Python都是这么写的;就说Python都是喜欢用Itter;这Python的写法也没有;就是一个;Python的习惯;如果样本大小不是批量数的整数倍;那需要随机剔除多余的样本吗;这个也是一个;细节的问题;就是说假设我有100个样本;我批量大小取了60;那么我第一个还能;第二个最后40个怎么办;有三种做法;最常见的做法其实是;拿到一个样本把后;就拿到一个小一点的样本;就是常为40的一个批量大小;这是我们这里的做法;是这样子做的;第二种做法是说;把最后一个不完整丢掉;这是第二种做法;第三个做法是说;其实是说;从下一个epoch里面补20个过来;要理解吧;就是说我我不够20个嘛;我再去随;在别的地方;再随地采一二十个过来补全;这是第三种做法;hello please stop;hello please stop;hello please stop;所以;问题22优化算法里面除以badge size;但是最后一个badge的样本没有那么多;对了这个就是一个;是的这是我们偷懒的;比如说实际上你的实现应该是;你应该除以到;你根据你真实的你拿进来那个批量多;多大你要除以他;这是你真实的真正的实现;这里我们就偷个懒;其实你就无所谓了;就是少一点点多一点点;而且我们这也是整除的;你可以我们生成了100个样本;然后我们的批量是等于10;所以我们除起来是整除了;所以没关系;但是你实际上;你应该是要去除你的实际样本的个数;你用Patouch的trend的话;它会帮你做这个事情;hello please stop hello;please stop hello please stop;提问题24学习率不做衰减吗;有什么好的衰减方法吗;我们没有做衰减;我们整个整本书都没有讲太多衰减;就是说衰减的意思是说;理论上;SGD要要收敛的话;那么需要不断的把学习率变小变小;变小变小;在实际上来说;你其实有很多种办法;你不做分解也问题不大;就是说是;比如说你用;我们之后会讲那种比较adaptive的学习;方法;就是说;他会根据你的t度的大小来调整学习;律师就是说你不做衰减也问题不大;所以你就说;我们可以先不讲这个事情;不讲这个细节;hello please stop;hello please stop;hello please stop;收敛的判断吗;要直接人为设置epoch大小吗;你可以判收敛;收敛很多种判法;一个是说我发现两个目标函数;两次迭代的目;两个epoch之间;目标函数变化不大的时候;我就可以收敛了;我可以这么判;就说;相对物质相对变化是比如说1%的时候;我就说停了;第二个是说我会拿;一个验证数据集;看一下验证数据的精度没有增加了;我也可以停;就这里我就偷个懒吧;就是说那你就看一下你眼睛;看一下就说实际情况下;实际;在真实的;训练中;通常来说这个是大家凭直觉选的;就取决你这个;一般来说;第一次训;训练的时候我会去看他;就说我就选一个比较大的吧;设100 比如说;要去看他的学习的曲线;我们之后会来给大家画;那个曲线长什么样子;我如果感觉他平了的话;我感觉;这个数据集感觉有点难;可能要100个EPOK;另外数据集可能就40个就差不多了;那我就下次我就知道;这个写100;这个写40;这是最简单的了;实际情况;就说你当然自动化一点;就是说根据你每一次精度的变化;或者是说;你的目标函数的变化;变化不大了;你就可以停;但是你多迭代一点没错的;就说你只要你算力支持;你就多跑一点;没关系就就;说就算你的loss没有下降了;可能他还在做一些微调;不学习;就说就说;你就说你读书对吧;读十遍可能差不多;你再读一遍也没关系;就这样子;hello please stop;hello please stop hello please stop;本本质上为什么没拥有SGD;是因为大部分实际loss太复杂;推导不出导数为0的解吗;只能逐个bitch去逼近;是的是这样子;就是说除了线性回归之外有显示解;别的所有都没有;有写字节的模型;我们也没必要真的花半年来给;大家讲了这东西;我就讲到今天就结束了;剃度就后面都不用讲了;但实际上来说;求解不了;就是说我们我们都是在解mp;就所有我们有意思的问题都是mp complete;如果你这个问题不是mp complete;用什么机器学习对吧;直接直接精确值求了;所以的话;你你如果能够直接解救出来;那就不算be complete了;哈哈哈对吧;OK;hello please stop;hello please stop hello please stop;问题26 为什么w每次要随机初始化;不能用同样的值呢;你可以用同样的值没关系;就是说你可以固定随机种子就说;但是你无所谓;就是说这个东西;;你随机或者你固定或不固定的没关系;就说我们就偷懒就不固定了;实际中有时候网络会输出lotter number;lotter number怎么出现的;为什么不是应付;数值不稳就是说因为求导于密;有有有除法;除法会导致你处处0;除应付呀;就是说会出现这个问题;涉及到就是;求导带我们会讲数值稳定性的问题;在后面一节;另一层最后一定要手动设置;初始之门;不一定就说他有默认的处置值;也挺好的;就我们之所以手动设施给大家说;我们要跟我们的之前的那个;从零开始实现能匹配上;就是这个意思;就我们之后就不会这么手动式了;因为收不过来了对吧;l的backward就是调用它的backup provocation;我们在之前自动求导里面有讲过;对最后一层复;里面最后一层就是为了print;我们就是为了print它;不需要清零;梯度清零是因为我们没有更新了;我们只run forward;没有run backward;所以不需要清零;hello please stop;hello please stop;hello please stop;每个batch计算的时候;为什么要把t图清零;是因为;排头局不帮你清;就是你算完t图之后;如果你不清零;它就在上面的t图上做累加;就一直累加下去了;;这个这个问题就是说还是not number问题;我们会有一专门的一章来给大家解释;所以大家不用急;我们会讲为什么要应付;为什么要not number;为什么会变成0;怎么所以这一块;我们会因为这个问题还挺;挺难的挺严重的;所以我们会;真的给大家解释一下;专门花一些时间;;
No.2 Softmax回归+损失函数+图片分类数据集
一、Softmax回归
1、Softmax回归
- Softmax回归;它是继续学习另外一个非常经典;而且重要的模型;虽然它的名字叫做回归;但是它其实是一个分类问题;
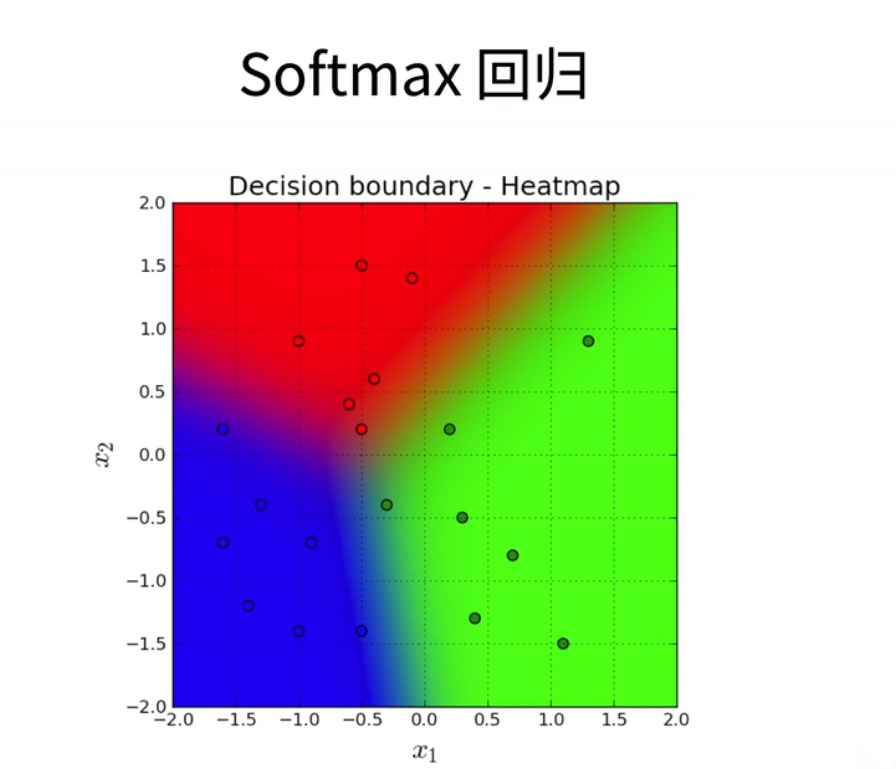
2、回归vs分类
- 我们来解释一下分类和回归的区别。之前,我们已经学习了线性回归,其中我们预测的是连续值,比如房屋的售价。而对于分类问题,我们预测的是一个离散的类别,例如判断一张图片里是猫还是狗。让我们通过几个例子来说明:
- 首先,一个经典的数据集是MNIST,它用于识别手写数字0到9,因此它是一个十类分类问题,我们需要将数字分类为这10个类别。
- 另一个非常经典的数据集是ImageNet,在深度学习领域引发了一系列重要突破。这个数据集包含100万张图片,每张图片都包含一个自然物体,通常是1000个不同类别中的一个,例如包括大约100种不同种类的狗。因此,ImageNet问题是一个包含1000个类别的分类问题。

3、常见分类问题
- 接下来,让我们来看几个典型的分类问题。首先,我们可以考虑使用显微镜图像来分类人类蛋白质。在这个问题中,有28个不同的蛋白质类别,我们需要根据显微镜图像将其分类为其中的一种。
- 另一个典型问题是,假设我们已经获得了一个软件的运行信息,我们希望判断它是否是一种恶意软件,以及如果是,那么它属于哪一种恶意软件类型。
- 还有一个经典问题涉及文本分类,例如,我们可以收集来自Wikipedia的评论,并尝试分类这些评论,以确定它们是否包含不雅内容。在这个问题中,通常有多个不同的恶意类别,总计有七个类别。

4、从回归到多类分类
- 回归和分类问题之间存在许多相似之处,但也有一些不同之处。在回归问题中,我们通常要预测一个连续的数值输出,这个输出的范围是一个自然数范围,比如房价预测。尽管输出值必须大于等于0,但实际上它可以具有不同的取值。在构建损失函数时,我们会计算预测值与真实值之间的差异,通常使用平方差作为损失函数,即预测值减去真实值的平方。
- 而在分类问题中,通常有多个输出。举例来说,如果我们要进行三类别的分类,输出不再是单一的数值(如O1),而是包含多个元素的向量(如O1,O2,O3),其中每个元素用来表示对应类别的置信度。因此,可以简单地认为,分类问题将从回归问题的单一输出转变为多输出,其中输出的数量等于类别的数量。

5、从回归到多类分类―均方损失
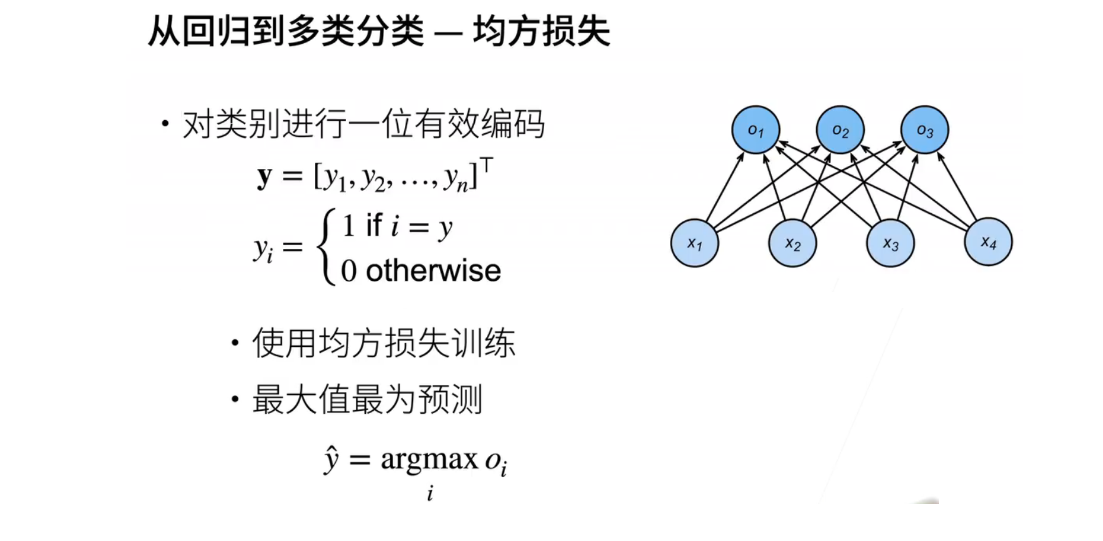
- 当从回归问题过渡到分类问题时,首先需要对类别进行编码。由于类别通常是非数值形式,如猫或狗,对n个类别可以使用最简单的一位有效编码方法。如果有n个类别,那么编码向量将包含n个元素,从Y1到YN,其中真实类别对应的元素(假设是第i个类别)等于1,其他元素全部设为0。一位有效编码表示只有一个元素是1,该元素的下标对应真实类别,其他元素为0。
- 使用这种编码,可以将分类问题转化为具有一位有效编码的回归问题,从而可以使用回归问题的损失函数进行训练。在训练好模型后,进行预测时,选择具有最大OI值的i作为预测类别,即argmax(OI)。
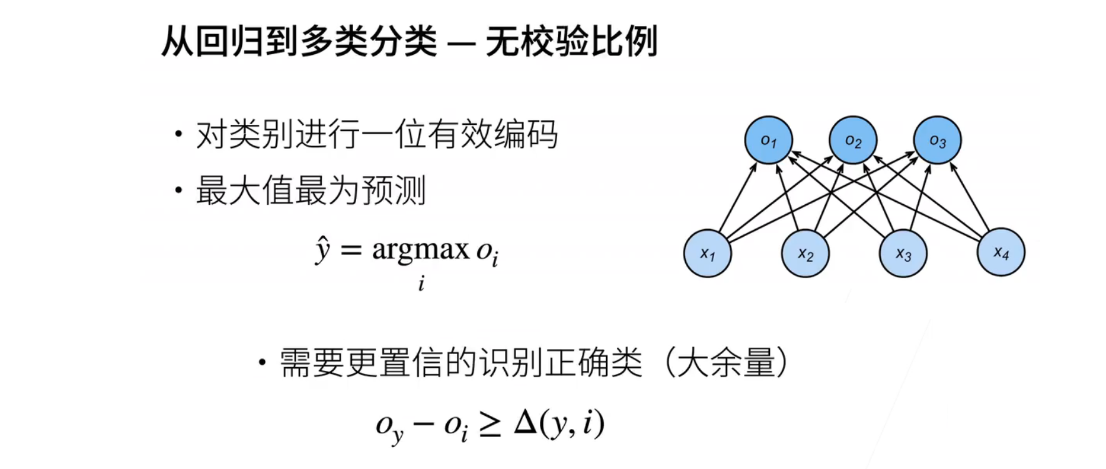
- 现在,让我们逐步从这个基础点过渡到Softmax回归。在分类中,我们通常不关心OI值的实际数值,而关心的是对正确类别y的置信度是否远高于其他非正确类别的OI值。这可以用一个数学不等式表示为OI - OI > delta,其中delta是一个预先定义的阈值,用于确保模型能够明显区分正确类别和其他类别。
- 此外,尽管OI的绝对值不影响相对值,但将OI的值映射到合适的区间可以使问题更简单。这是为了让后续计算更加方便。
6、从回归到多类分类―校验比例
- 当我们希望将模型的输出转化为概率分布时,可以引入Softmax操作。这将Softmax函数应用于模型的输出向量o,得到一个新的向量y hat,其中y hat是一个包含n个元素的向量。这个向量具有一些特性:每个元素都为非负值,而且所有元素的总和等于1。
- 具体来说,y hat中的每个元素y hat i等于o中对应元素的指数。指数运算的好处在于它可以将任何值转化为非负值,然后我们将这些非负值归一化,除以所有指数的总和,以确保y hat中的所有元素总和为1。这使得y hat 成为一个概率分布,与真实标签y的表示方式类似。
- 我们知道真实标签y也可以视为概率分布,因为它的一个元素为1,其他元素为0,而且所有元素非负且总和为1。然后,我们可以通过比较真实标签y和模型的预测y hat 之间的差异来计算损失。

7、Softmax和交叉嫡损失
- 一般来说,我们使用交叉熵(cross-entropy)来度量两个概率分布之间的差异。假设我们有两个概率分布p和q,我们可以使用H(p, q)来计算它们之间的交叉熵。对于离散概率分布,如果它们有n个元素,那么交叉熵的公式可以表示为:H(p, q) = -Σ (p_i * log(q_i)),其中i从1到n求和。
- 在分类问题中,我们通常使用交叉熵损失来衡量预测概率分布与真实标签之间的差异。对于真实标签y和预测标签y hat,交叉熵损失可以表示为L(y, y hat) = -Σ (y_i * log(y hat i)),其中i从1到n,n是类别数量。需要注意的是,对于真实标签y,只有一个元素为1,其余元素都为0,因此交叉熵损失的求和可以简化为L(y, y hat) = -log(y hat j),其中j是真实类别的索引。
- 关于损失的梯度,如果我们对损失L对于y hat进行求导,那么梯度等于y hat - y。这意味着我们通过不断减小真实标签y和预测标签y hat 之间的差异,来更新Softmax函数的输出,使其更接近真实标签y。这样我们就能不断降低损失。

8、总结
- 下面是对Softmax回归的介绍:虽然它称为回归,但实际上它用于多类别分类问题。在这个方法中,如果我们有n个类别,我们需要n个输出。Softmax操作用于将每个类别的分数转化为概率,确保它们是非负的且总和等于一。最后,我们使用交叉熵损失来度量我们的预测与实际标签之间的差异,作为损失函数。这就是Softmax回归的工作原理。

二、损失函数
1、损失函数
-
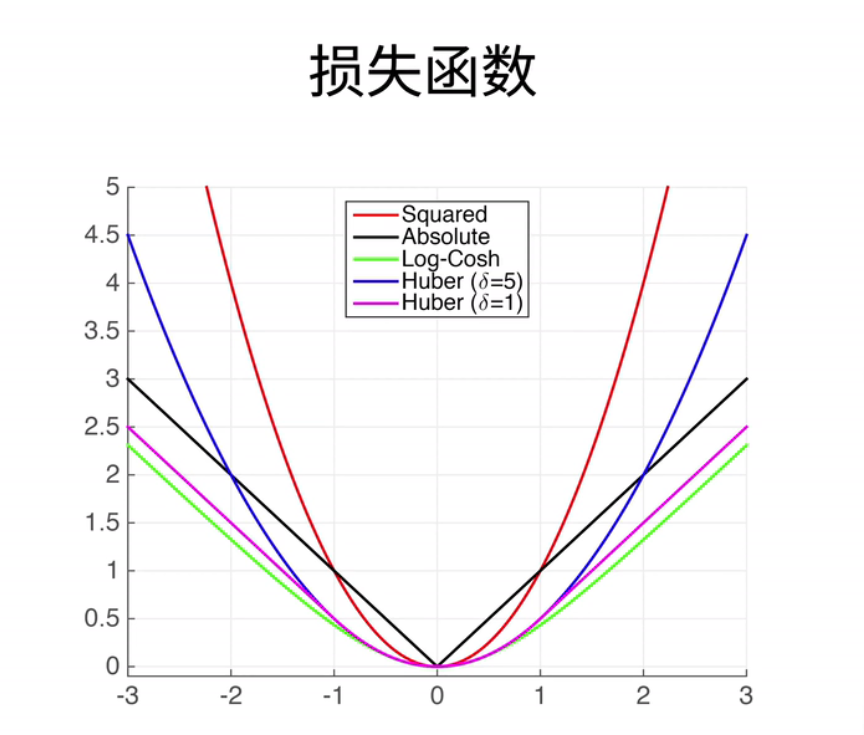
损失函数;用来衡量预测值和真实值之间的区别;是机器学习里面一个非常重要的概念;这里简单介绍三个常用的损失函数
2、L2 Loss
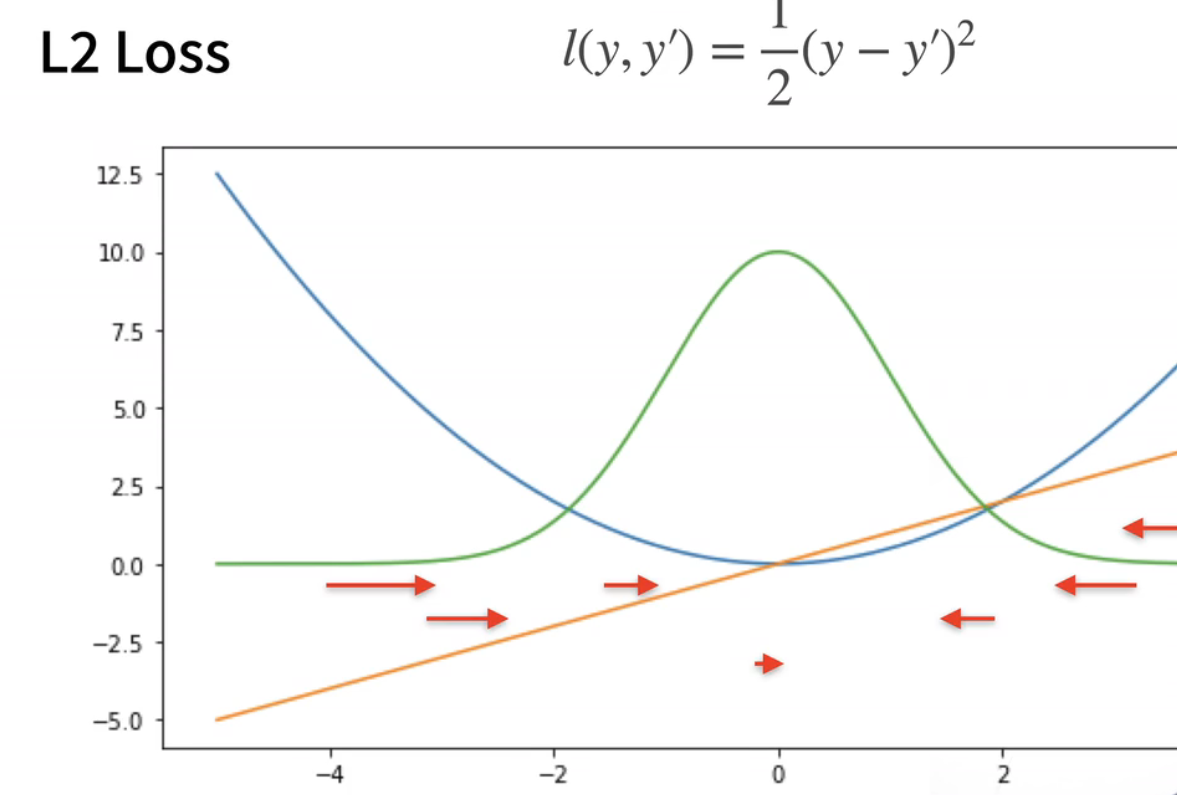
- 我们已经介绍过的L2损失,又叫L2 loss。它的定义非常简单,即真实值y减去预测值,我们用y hat来表示。然后再平方,再除以2,这里1/2的目的是为了在求导数时,将2和1/2相互抵消,最终变成1。
- 接下来,我们画了三条曲线来展示这个损失函数的特性。蓝色的曲线表示当y等于0时,随着预测值y hat的变化,它是一个二次函数。绿色的曲线表示它的四次方函数,也就是1的负4次方。虽然我们没有详细讲解四次方函数,但它在统计中是一个重要的概念,它表示一个高斯分布。
- 橙色的曲线表示这个损失函数的梯度。我们知道它的梯度是一个一次函数,且穿过原点。在梯度下降时,我们根据负梯度的方向来更新我们的参数。可以看到,当预测值y hat远离真实值y时,梯度较大,因此参数的更新幅度较大。当y hat逐渐接近真实值时,梯度的绝对值变得越来越小,这意味着参数的更新幅度也变得越来越小。然而,这并不一定总是理想的,特别是当我们对远离原点的数值进行更新时,我们可能不想要那么大的梯度。
- 因此,另一个选择是考虑…
3、L1 Loss
- 绝对值损失函数,也叫L1 loss,其定义非常简单,即预测值减去真实值的绝对值。当然,反过来也是一样的。蓝色的线仍然代表损失函数的曲线,即当y等于0时的样子。绿色的线代表其四次方函数,具有一个尖峰,位于原点处。有趣的是其导数,可以看到,当y hat大于0时,导数为常数1,当y hat小于0时,导数为-1,同样是一个常数。我们之前提到过,由于绝对值函数在0点处不可导,因此其梯度可以在-1和1之间变化。因此,这个损失函数的主要特性是,无论预测值距离真实值有多远,梯度始终是常数,因此即使预测值相差很大,权重的更新也不会特别大,这可以带来稳定性上的好处。然而,它的不足之处在于,我们之前提到过,0点处不可导,而且在0点附近存在剧烈的梯度变化,这种不平滑性导致了当预测值和真实值靠得很近时,尤其是在优化末期,可能会变得不太稳定。总的来说,无论你的预测值有多远,这个损失函数的梯度基本上都会帮助你朝着原点移动,这可以提供更多的稳定性。

4、Huber
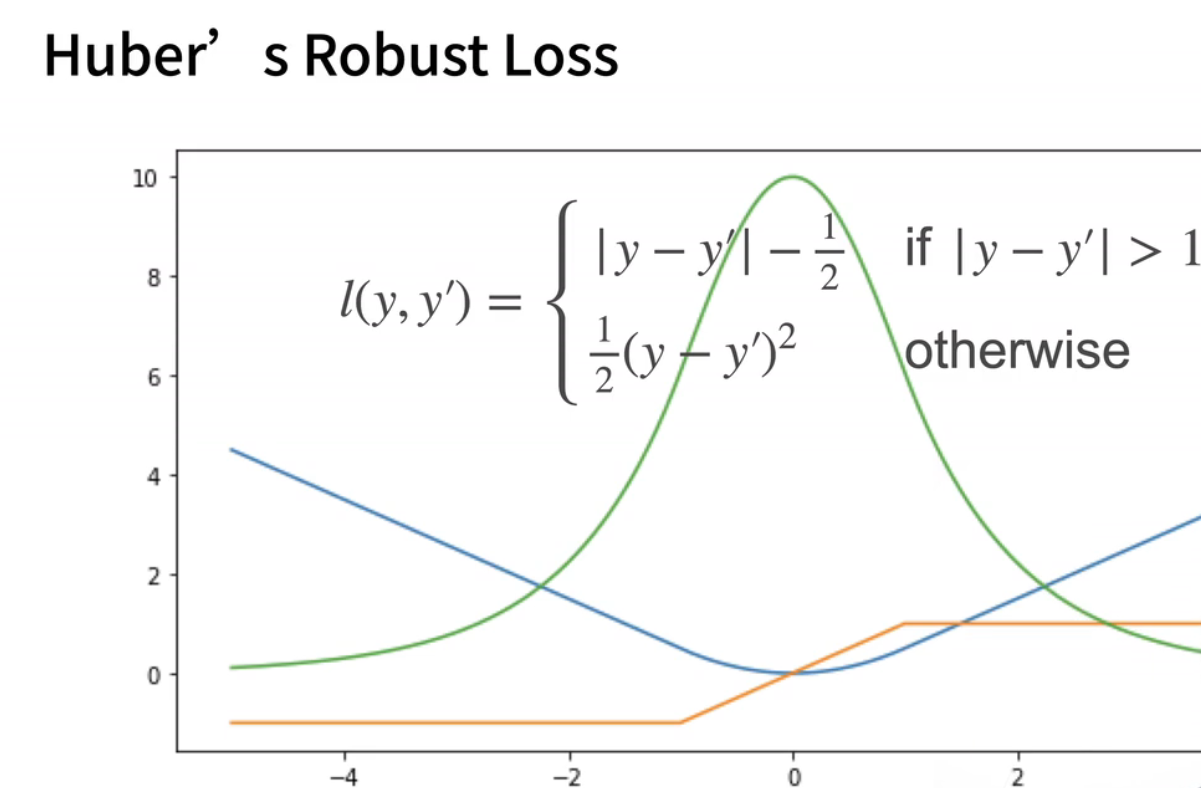
- 我们可以提出一个新的损失函数,结合了绝对值损失和平方损失的优点,同时避免了它们的不足。让我们举个例子,这个损失函数被称为"Huber鲁棒损失",其定义如下:当我的预测值和真实值差距较大,即绝对值大于1时,我使用绝对值误差,即y减去y hat的绝对值。通过减去fg,使曲线可以连接起来。当你的预测值和真实值靠得很近,即小于等于1时,损失变成了平方误差。你可以看到我的南侧是曲线,在正一和负一之间,它是一个二次函数,非常平滑。但是在之外,它是一条曲线,绿色线是损失函数的导数,你可以看到它仍然类似于高斯分布,但不像绝对值损失那样,在原点附近有一个尖峰。
- 导数是最值得关注的地方,你可以看到,当y hat大于1或小于-1时,导数是一个常数,而当y hat位于这两个值之间时,它是一个渐变的过程。所以它的好处在于,当你的预测值和真实值相差较远时,不管如何,它的梯度都能够以相对均匀的力度帮助你朝着原点回归,但是在你靠近原点的时候,也就是在优化的末期,它的梯度绝对值会变得越来越小,这样可以确保你的优化过程相对平滑,避免出现太多数值上的问题。
- 所以,我们已经介绍了三种相对简单的损失函数,不论它们多么复杂,我们同样可以通过类似的方法来研究它们的特性,特别是在预测值较远和较近的情况下它们的作用。最简单的情况下,我们可以通过它们的函数形状和梯度形状来分析这些特性。这就是关于损失函数的介绍。
三、图片分类数据集
代码
四、Softmax回归从零开始
代码
五、Softmax回归简单实现
代码
六、QA
第一个问题是说;能提一下soft label的训练策略吗;以及为什么有效;soft label是说嗯;刚刚有讲到怎么样用;一位有效来表示一个标号;就是说有n类的话;就把变成一个很长的项量;其中只有正确那一类为一;剩下的那所有的全部变成0;所以呢然后用一个Softmax;去逼近这个乘以一的分布;但是它的问题是什么呢;他的问题是说;用一用了指数的话;很难用指数;去逼近一个一;因为指数变成一的话;想让他完全变成一的话;必须是的那个输出;几乎接近于无穷大;而剩下的东西;都很小这就是挺难用;soft Mac是逼近一个0和一的;一个极端的数值;所以他提出了一个方案;是说那就不用用那么极端吧;那就说如果是正确那一类;那就把记成0.9;剩下那些不正确的类;那就是0.1;除以n分之一;这就是;soft label这样的好处是说;使得用;Softmax真的去完全拟合那个0.9;和那些很小的数的时候;是有可能的;这个是一个常用的技巧;在图片分类里面;这是默认的大家会使用的一个小trick;第二个问题;Softmax回归和logistic regression;它是不是一样的;如果不一样的话;哪些地方不一样;其实可以认为它是一样的吧;就是说;logistic regression就是一个;可以认为是一个;当只有两类的时候;做Softmax会怎么样;就是说等于是输出只有两个;一个正1;一个-1;但是注意到是说的Softmax;它的加起来是等于一的;所以如果就做一个0和1分布的话;根本不需要管;只要预测为0的那个或者正一;或者-1 只要预测-1的那一个类;因为正一;只要预测了负1;正一那就一定是一减去那个概率;这就是Logistic regression和Softmax的区别;所以Logistic regression;虽然是一个二分类的问题;但是呢它实际上只要输出一个;元素;可以是要么是对正正一类的预测;要么是-1类的预测;那么剩下那个类;那就是等于一减去它;所以就是可以认为是;Logistic regression是Softmax regression的一个;特例;一般来说;在;接下来深度学习中很少遇到;两分类的问题;所以就是直接跳过了logistic regression;直接讲Softmax回归;第三个问题和第二个问题;其实是一样的;第四个问题是说;为什么使用交叉伤而不用相对伤;或者别的;信息衡量标准;大家如果学过的话;那知道;相对上;mutual information就表示的是一个两个;统计两个概率之间的一个区别;它比交叉上的好处是说它是没有;它是一个对称的关系;就是说;现在HPQ它不等于HQP;但是相互上呢;就是IPQ是等于IQP的;至至于为什么不用呢;其实也没有特别大的原因;不用户信息最大的问题;是不好算;那东西算起来;不如加销商来的那么简单;对于来讲;其实真的只关心一个;两个分布的一个距离;就跟讲过的手势函数一样;用l one;用l two或者用Harbor的loss;其实差不多;最后的最后会选一个;算起来相对来说简单一点的;第五个问题;why产业lock;why hat;只关心正确的类;不关心不正确的类;如果不关心不正确的类的效果;有没有可能更好呢;其实不是不关心不正确的类;是因为那个;那个哇;hot的那个编码;就是把剩下的类的概率变成0了;所以导致计算的时候可以忽略掉;不正确的类;如果使用之前提到的;soft label那就是不正确的类;它是;也是有存在一个非0的概率的情况下;那确实会关心不正确的类了;OK再刷新一下;看看还有没有;别的问题;这样的n类问题;对于一个类别来说;是不是认为只有一个正类;n减一个负类;会不会;类别不平衡呢;会;会有这样子的情况;但是相对来说;好处就是说;可以看到刚刚那个损失函数;如果是用01这个编码的话;其实并不关心别的类的一个;别的类会怎么样;所以只关心当前类;或者是说;其实大家不用关心说是不是不平衡;要关心的是说是不是存在一些类;他那些类;没有足够多的样本;没有足够多的样本;那就会比较麻烦;如果每一个类有足够多的样本;比如说;image net每一个类;大概都有5,000个样本的情况下;那么其实去每个类还是差不多的;;另外一个问题是说;损失函数的红色箭头;和橙色的线之间的关系;再讲解一下;可以来可以讲解一下;就是说其实就是一个很直观的表示嘛;就是;这个箭头就表示还记不记得;就是在讲梯度下降的时候;每次有一个点;然后沿着这个点;沿着这个往往前走一步;那么这个不长取决于两个东西;是不是;一个是的梯度那个本身的大小;一个是的学习率;这里假设;的学习率是固定的情况下;那么呢那么的那个不长;就真的取决于的梯度;那些数字的大小;数值大小就用橙色线来表示;所以这个线就意味着是说;不管是在正一还是-1;那个梯度的绝对值就是那个长度;其实是一样的;所以在不管哪一个地方往前走一步;的;在基本上学习率在不变的情况下;那么的步长都差不多;所以这里就意思是说;每个红色的箭头的步法都差不多;假设要往前走的话;比如说是l two lost的话;那么可以看到是说;跟原点隔得比较远的地方;的梯度的绝对值比较大;比较大的话;在学习率固定的情况下;那么这个布场就会显得会大一;点反;反过来说;到了快到0点的时候;的绝梯度的绝对值变小;那么的步长也会变小;就说可以认为是说;这个损失函数;是怎么样把一个远的一个结;拉向的最优解l two的话;就是说如果跟离得很远;那就会尽力的;把很快的把拉过来;如果是l one的话;那就是一个均匀的速度把拉过来;OK;问题八是说;对于Ms SE和最大四然的估计;能不能稍微提一下;其实和第九问题是差不多的;就是说;四然函数的曲线是怎么得出来的;这个之所以没有讲;是因为整个这一块;其实统计里面的概念;;其实尽量的没有涉及到太多的统计;因为为什么;是因为;统计;是可以用来解释模型的一个工具;但反过来讲;深度学习在后面的模型;跟统计没有太多的关系;所以这一次主要讲的是;线性代数;因为的所谓的数据结构;是一个线性代数;所以可以大概简单讲一下;最小化的一个损失;就等价于最大化的一个自然函数;就说自然函数;就是说这个;有个模型;然后这个去;给定这个数据的情况下;这个模型就说模型;所谓的模型就是的权重了;出现的概率是有多大;就是那么需要最大后;也给定观察到的东西;要找到一个模型;使得给定这个数据出现的概率;是最大的最合理;的解释;所以呢就是说;可以看到这个;这个线;虽然是要最小化的;损失函数;也就是等价于最大化;那个最大4然函数最大4然;在这里其实可以等加是一个;那统计上来就要叫做一个指数;family的一个分布;所以的话;就是有可以对应到概率那一套东西;那并没有特别讲;所以大家可以去看一下书;书里面确实是有讲4还是怎么样子;如果大家想更深刻理解的话;可以学一下统计;或者说;统计学习就是statistic learning;会稍微讲一点点;但是不会深入太多;OK;第十个问题其实也有讲过;就是其实就是说当的;就说这个问题是说;在不同的损失函数;下降的速度;和昨天讲的学习率的关系是什么样子;昨天理解的学习率好像是梯度;下降的步长;步长和速度有点搞不清;就是说;刚刚也讲过;那个其实那个w;每次对他的做更新的时候;需要两项对吧;一项是的负的梯度方向;一项是的学习率;所以要;所以就是被两个地方控制;一个是那个梯度;的每个数值有多少;另外一个是说的学习率;就是是人为控制的;所以呢;这里的理解是说;假设的学习率是固定的情况下;那么不同的损失函数;会导致算梯度的那个值会发生变化;就说在别的全部固定就是学;习率固定的情况下;不同的损失函数;会导致在不同的地方;会带来不一样的梯度的那一些值;使得的走的那个;每次走的那个步伐会有点不一样;第11个问题是说all the regression;其实不是特别理解;all the regression是什么;假设是说rankingranking;所谓的ranking就是说得去排序;说a是应该排在b的前面;那就意味着说;其实并不关心的概率什么样子;的数值是什么样子;只关心的相对值;其实可以用Softmax来做;其实也问题不大;但是可以把它做成一个ranking的;问题ranking就是用margin来做;其实说句脏话会有一点点区别;但实际;使用中区别不那么大;其实那些区别跟的数据;跟的最后的那个模型;其实差别还是挺明显的;所以每个地方都有区别;所以当然可以用Softmax;总是可以用的;OK应该是这也是的;所有问题再刷新一下;刚刚有同学问到;是在直播还是在录播;现在是在直播;不过今天确实想试一下;是不是能提前录一下;效果会不会好;就是其实在大概3个小时之前;录了几段;主要有两个目的;刚好时间还有24分钟;应该来得及;聊一下这个;整个是怎么设置的;今天想试一下录制一下;为什么呢;是因为前面几次;有一;次是摄像头;就相机有点发热;另外一块就是;有一次是说解释一个东西;其实是解释错了;还有一次其实是;的;有一个的notebook里面没有;那个slides没有写出来;所以感觉这些东西都会给直播;给大家浪费大家时间;特别是浪费大家几分钟时间;所以呢在想说;先试着先录一次;录一次的话如果中间出现问题;可以把它剪掉;所以就说不用去节省大家的时间;第二个也是;看一下;自己能不能承受这个哈的开销;因为直播容易一些;就直播就讲过去;反正一个半小时;讲也是讲站;站在这里也是时间也花掉了;所以要去录的话;其实还得多花一两个小时;在想;能不能承受这个时间;因为主要是周末干这个事情;周末现在是还是在疫情期间;跟太太两个人;在周末主要的活动是带了两个娃;一个4岁一个一岁;基本上是要等他睡午觉的时候;能够抽一点时间来做一点概念事情;所以就是想看看;能不能在那个睡午觉;他的一个半小时里面;能不能压出来;能把录一段;给大家提供更好的体验;当然希望是不要录;希望直播能达到今天;除了今天录播少放;有个order没放对之外;希望直播能达到的;录播的效果;但是目前来说;这个是;这个也;是一个业余;想做到一个因为想露脸;露脸的话;因为露脸主要是会有一点交互性;大家会觉得可能会呃;就motivate去看一点;当然不是长得怎么样;所以呢;在想就说因为要为了露这个脸;所以导致整个其实挺麻烦的一个事情;给大家可以看一下;现在这个set up是什么样子;其实现在车库里面;车库这个地方真的是;冬天很冷;夏天很热;所以所以可以看到是说;这里是一块绿布;这导致的那个背景的透明;然后呢这里有个灯;这个灯其实也不是那么的好;其实一直想买一个灯;这个灯呢;一个新品;然后到等了两个月还是没到货;认为可能是疫情的缘故;所以那个灯感觉没造出来;所以这个灯有时候会;觉得不是很亮;就背景有会有一点点灰;然后下面其实更麻烦;下面有一个相机;这里有个Mac;这里还有一个MacBook;然后那里有显示器;的屏幕是在这个地方;这里有一个摄像头在;在这个地方有个麦克风在这里;下面其实本来再来一个iPad;本来如果要手写;然后可以用它;所以整个设置;其实是挺麻烦的一个设置;经常出错的概率特别大;所以在想说;好在确实能;哎还而且这个设置会在不断的变;每天可能会想一想说;是不是有办法显得更专业一点;做一件事情就;是尽量做到最好;觉得这个也是想;不管做什么事情;虽然这个东西;可能觉得找一个专业人士来帮;就解决了;但觉得需要去;这门课就动手学嘛;就是就是;要去动手不管什么事情都去动手;这个是的一个哲学;OK;所以尽量;尽量;还是在学习怎么样做比较好的;课程然后;确实比较得心应手了;就直接直播就行了;哈哈这样子也简单一点;但是确实觉得还是内容有限;因为多花一个小时;如果有100个人或1,000个人;能够节省5分钟或看的更好的话;就还见了;就说number做比较好的没得问题;这样子也简单一点;但是确实觉得还是内容有限;因为多花一个小时;如果有100个人或1,000个人;能够节省5分钟或看的更好的话;觉得还是值得;OK所以;来直接来切换到的问题;是说第一问题12是说;执行这个下载命令后显示HTTBL;这个东西还真不知道;这个他是用的是;touch的自己的官官网网网下载;哈哈;希望他不是放在Google上面哈哈;这样子可能会下载会比较麻烦一点;当然如果不行的话;就是自己手动下载也行;可以看一下拍拖局的网页上;怎么把这个数据集手动下载;问题是3;this loader的number of work是并行的吗;是的就是说取决于;的实现;应该是;拍talk应该是用的是进程来实现的;就是说的number of works设成是4的话;那么会在后端开4个拍摄的进程;来帮做并行;问题是写4也是一个相关的问题;这个;直接写4是不是不好;哦;进程这样子简单;还是有必要写嘛;是不是不好;其实其实也可以直接写了;这个没关系;之前之所以这是有个历史原因;之所以做了这个函数;是因为在以前在早点版本里面;他Windows不支持;所以在函数里面要判一下;如果是Windows的话;不要用;只能不能开;躲线程;躲进程所以;然后就一直保留下来了;但写不写都没关系;觉得不写没事;;另外是方差0.01有什么讲究吗;没有什么讲究;就是;现在没有什么讲究;之后会有;现在就选了一个比较小的值;之后会来解释一下;应该是下下节课会来解释一下;方差这个东西其实是挺有讲究的;对深度审计网络;方差是很重要的一件事情;但是只是放在这里;大家知道这是一个;超参数就行了;问题是7;pitoge训练好的模型;在测试的时候;不论是badge size设备一还是更多;测试的时间差不多;如果正常理解;如果设成4;不应该就是一的4倍速度吗;当然不是的;就是说;就是说不管bitch size等于几;的计算量是不会发生变化的;只是说唯一的发生变化的是说;的变形度;计算的时候的变形度是不是能增加;使得的整个;这执行的效率能不能增加;所以说;如果badge size变大变小都没区别的话;很有可能是说;这个模型其实就很小;本来就变形度不够;所以就看不出区别;但一般来说;而且在CPU上;可能大家也看不出太多区别;这个主要的区别是在于;在GPU上会有比较大的区别;因为GPU上;现在都是上百或上千个核;当然会有一点区别;CPU上可能确实没区别;问题是把这两个等号等号相连;起什么作用;应该就是Python的pan;两个东西是不是相等;就是看每个元素之间是不是相等;在;数据操作那一节讲过这个问题;大家可以回顾一下;;为什么不在AQC的函数里面;把除以nonse y呢;之所以不做这个事情是说;有可能还记不记得;如果去读一个badge的时候;最后那个badge很有可能是没读满的;如果在ACUS;ACUS也就是说要对n个batch;然后一直算下来;如果都除了的话;那其实它如果最后一个batch;它的呃batch size;它的number of examples;它不等于那个batch size的时候;那这个是不正确的;所以应该是把;所有东西的正立和负立;在所有的群面加起来;然后最后再除是等价的;;CMP的typey;type是必要的吗;可以可以去试一下;可以试一下必不必要;可能是不必要的哦;就是说这个是给代码给代都能让;就去让一下吧;而且其实里面代码不很多;代码其实觉得是有一点点多余的;可以去尝试去简化它;之所以写成那样子;很多时候有很多一些历史原因;很多时候是老的package版本不支持;如果做的比较早的话;;拍拖解释每三个月更新一次的话;那么新的版本也许支持了;但不一定是能改过来;但还在;联系拍托起团队说;把整个;这本书;放进他的官方的一个测试里面;这样子他的可以帮也来看一下;IQC函数能不能再讲一下;觉得IQC函数可以去;仔细看一下;其实还是比较简单的一个;计算嘛好;之后会再讲一次;IQC就是在GPU上怎么算;所以可以可以先看一看;如果还没看懂;下一次再讲IQC的时候;可以再听一听;在计算精度的时候;为什么用Evo将模型设成评估模式;是因为;其实不设没关系;是为了一个好的习惯吧;就设一下吧;就是说设成Evo模式的话;那就是他默认会不去开不去对的体;他就知道不要算剃度了;那很多跟剃度相关的事情;可以不用做;性能上可能会好一点;但是觉得不设也没关系;这里的;w和b是怎么从网络模式中抽出来;放进Updator的;其实不是很知道;是讲哪一个实现;如果是讲的;的从0开始的实现的话;就直接拿出来放进去;w和b是创建的;如果是讲的是NMOJ的实现的话;在构造那个automizer的时候;是把net的点parameters;但net点primetors;就把所有的w和b拿出来;放进了它的呃update里面;这就是做step的时候;就已经知道这些;所有的模型了;问题23在多次迭代之后;如果测试精度出现上升再下降;是过离合的吗;是不是可以提前终止;很有可能是过敏核了;但是可以再等一等;如果确实一直是下降的话;那有可能是过敏核;嗯通常的;可能会后面会讲一些策略;让来尽量的避免;一个办法是说;可以通过比较好的去微调呢学习率;能够呢避免一些事情;当然可以通过讲各种政策项吧;之后会来讲这种实际的;碰到这种情况应该怎么办;而且会有竞赛真实数据;大家都来跑;大家都来跑的好处是说;因为现在是来讲来讲;就是就讲很标准的一些模型啦;但如果做竞赛的话;希望是说;大家都能来分享;给定个数据机;大家分享不同的模型;调彩的一些观察;这个事情是想做一个竞赛;让大家来做;事情就是大家把各种学到的;东西去试一下;然后以后碰到了新的问题;可以一起来讨论;CNN的网络学习到底是什么信息;是纹理还是轮廓;还是所有内容的综合;说不清的那种;还没有讲CNN;cn是接下来的话题;会讲到所有cn里面;从80年代到最近的一些模型;但如果大家懂得就说;懂的话就是说;其实也不好说cn学到什么;目前至少几年前;大家觉得cn其实主要是学纹理;轮廓他其实不那么在意;OK但是雪大龙纹理;纹理也不错;纹理就人看纹理不那么仔细;但计算机看纹理其实是非常强的;;是不是要对全列阶层的输出做成l to;规划;对最后的损失和精度会有什么影响;会专门有一节讲这一个东西;这是一个很重要的一个项;通过规划来控制过;喝;可以稍微等一下;等到应该是下周或下;下周没课;下周不是长假嘛;下下周应该会讲到;应该是下下下周;下周要讲赶制机;自己实呃;实现的Softmax和拍拓取实现的;Softmax谁快;这个东西就比一下嘛;呃;但很有可能他实现的稳定性要高;可以去看的书;书里面有个练习题;来跟大家讲;说为什么这么实现;会有一点的问题;有数据精度的问题;但是说谁快;大家一定要去比一下;千万不要信;说说快;说快;这些东西;都是;都是很主观的一些事情;如果是自己的图片数据集;需要怎么做才能用于训练;怎么样根据本地图片;训练集和测试集创建迭代器;这个可以去看一下patot文档;里面有从文件;就是说怎么办呢;最简单就是说;比如说的图片有10个类;有猫狗;马呀什么;就猫创建一个文件夹;狗创建一个文件夹;然后;把猫的图片放在猫的那个文件夹下;狗的图片放在狗的文件夹下;然后呢;拍拖写;能够说把的上一层目录告诉他;他就去扫一遍;是能够直接读进来的;可以去看一下排头局的文档;其实不管Tesla Pro还是msnet;它是都是支持这样子的一个操作的;另外一个问题就是说;在后续讲解;和现在英文版的内容是一样吗;哈看了一下;英文版有1,000页;哈哈是的;尽量把;在不断地把英文版翻译到中文版;然后;希望这个课能够把整个内容讲完;但可能会不会去讲推荐系统;因为为什么;是因为;推荐系统觉得写的还不那么好;还一个真正的教科书;能被好的大学采用作为教科书;那个还有一定的差距;所以那一章有一两章觉得;质量还不那么高;所以可能会这次会不会讲;但接下来会;找这方面的专家来继续往下写;这样子如果;到了觉得;非常专业的一个程度了;好可以开始来给大家讲一讲;Softmax究竟呢学到了什么;它的解释性可以怎么理解;有没有指标;可以衡量神经网络的解释性;这一块如果想理解的话;Softmax的话;还是有机会的;就是说还没有讲深度神经网络;所以只讲了一个Softmax回归;大家可以去看一下;如果想真的知道话去看一下;统计学习就是statistic learning;就说它里面是有很多可解释的;对于整个模型的capacity;他的convergence各种nonability;它都是可以做的;所以在可以去参考一下;那些相对应的数;这里;就不会特别深入的讲这一块了;因为想法还是说;给大家讲一下最基础的模型实现一遍;然后大概差不多了;就往前走;因为Softmax回归越好;线性回归越好;那都是;50年前的东西了;跟现在的神经网络确实差的;虽然本质上没有区别;但是他的各种细节还是差别比较大的;所以想尽量的快速的往前走;所以这一课;这个课不会那么的去讲;一些理论性的东西;所以这个也是这个课的局限性;大家理解;这个课其实很;是在讲一点点数学的前提下;尽量的往实用走;就是讲这是什么;怎么实现;怎么用然后还有一点点东西;还讲一下一些数学;为什么是因为如果纯纯讲数学;大家早就走掉了;哈哈哈;因为毕竟不是在尝试过在;book里的统计系;就是两年前在;UC book里的统计系;那也是世界上最好的统计系了;Michael Jordan;余斌;他都在那里;给统计系的本科生讲数学;大家都觉得哎呀这个东西有点难;所以觉得还是嗯;就是尽量的;使用化一点;这是的这个课程;OK来;最后刷新一下;如果这是所有的问题的话;今天刚好讲到这里;时间上刚好也是来最后看一眼;应该;;