文章目录
- 统计学习方法 条件随机场
- 随机场
- 马尔可夫随机场
- 定义
- 因子分解
- 条件随机场
- 定义
- 参数化形式
- 简化形式
- 矩阵形式
- 概率预测问题
- 前向-后向算法
- 概率的计算
- 期望值的计算
- 学习问题
- 改进的迭代尺度法
- 拟牛顿法
- 解码问题
统计学习方法 条件随机场
学习李航的《统计学习方法》时,关于条件随机场的笔记。
条件随机场(conditional random filed, CRF)也是一个条件概率分布模型,即给定一组输入随机变量条件下另一组输出随机变量的条件概率分布,其特点是假设输出随机变量构成马尔可夫随机场。
这里仅仅讨论 CRF 在标注问题上的应用,因此主要讲述线性链条件随机场。此时模型形式为对数线性模型,其学习方法通常是极大似然估计或正则化的极大似然估计。
随机场
随机场:随机场是由若干个位置组成的整体,当给每一个位置中按照某种联合分布 P ( Y ) P(Y) P(Y) 随机赋予一个值之后,其全体就叫做随机场。例如,我们有一个十个词形成的句子需要做词性标注,这十个词每个词的词性可以在我们已知的词性集合(名词,动词等)中去选择,当我们为每个词选择完词性后,这就形成了一个随机场)。
马尔可夫随机场
马尔可夫随机场,也称概率无向图模型,是以无向图的形式表示联合概率分布。
马尔科夫随机场是随机场的特例,它假设随机场中某一个位置的赋值仅仅与和它相邻的位置的赋值有关,与其不相邻的位置的赋值无关。例如,我们假设所有词的词性只和它相邻的词的词性有关时,这个随机场就特化成一个马尔科夫随机场。
定义
概率无向图模型:设有联合概率分布 P ( Y ) P(Y) P(Y) ( Y ∈ Y Y\in\mathcal{Y} Y∈Y 是一组随机变量),由无向图 G = ( V , E ) G=(V,E) G=(V,E) 表示。在图 G G G 中,节点表示随机变量,边表示随机变量之间的依赖关系。如果联合概率分布 P ( Y ) P(Y) P(Y) 满足成对、局部或全局马尔可夫性,则称此联合概率分布 P ( Y ) P(Y) P(Y) 为概率无向图模型(或马尔可夫随机场)。
成对马尔可夫性:设 u u u 和 v v v 是无向图 G G G 中任意两个没有边连接的节点,其分别对应随机变量 Y u Y_u Yu 和 Y v Y_v Yv ,其他所有节点为 O O O ,对应的随机变量组为 Y O Y_O YO 。成对马尔可夫性是指给定 Y O Y_O YO 的条件下 Y u Y_u Yu 和 Y v Y_v Yv 是条件独立的,即:
P ( Y u , Y v ∣ Y O ) = P ( Y u ∣ Y O ) P ( Y v ∣ Y O ) P(Y_u,Y_v|Y_O)=P(Y_u|Y_O)P(Y_v|Y_O) P(Yu,Yv∣YO)=P(Yu∣YO)P(Yv∣YO)
局部马尔可夫性:设节点 v ∈ V v\in V v∈V , W W W 是与 v v v 有边连接的所有节点, O O O 是除 v v v 和 W W W 外的所有节点。局部马尔可夫性是指在给定 Y W Y_W YW 的条件下 Y v Y_v Yv 与 Y O Y_O YO 是独立的,即:
P ( Y v , Y O ∣ Y W ) = P ( Y v ∣ Y W ) P ( Y O ∣ Y W ) P(Y_v,Y_O|Y_W)=P(Y_v|Y_W)P(Y_O|Y_W) P(Yv,YO∣YW)=P(Yv∣YW)P(YO∣YW)
当 P ( Y O ∣ Y W ) > 0 P(Y_O|Y_W)\gt 0 P(YO∣YW)>0 时,也可以表示为(这样比较像 Markov 性):
P ( Y v ∣ Y O , Y W ) = P ( Y v ∣ Y W ) P(Y_v|Y_O,Y_W)=P(Y_v|Y_W) P(Yv∣YO,YW)=P(Yv∣YW)
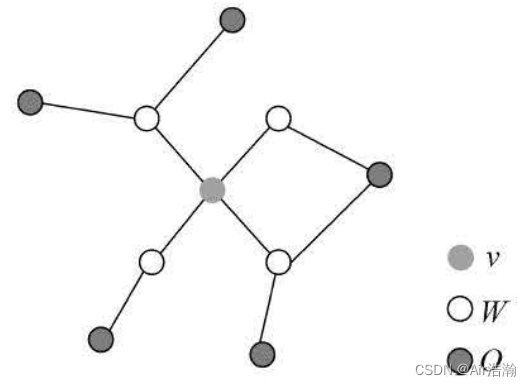
全局马尔可夫性:设节点集合 A A A , B B B 时在无向图中被节点集合 C C C 分开的任意节点集合(即删去 C C C 后, A A A 和 B B B 不连通) 。全局马尔可夫性是指给定 Y C Y_C YC 条件下 Y A Y_A YA 和 Y B Y_B YB 是条件独立的,即:
P ( Y A , Y B ∣ Y C ) = P ( Y A ∣ Y C ) P ( Y B ∣ Y C ) P(Y_A,Y_B|Y_C)=P(Y_A|Y_C)P(Y_B|Y_C) P(YA,YB∣YC)=P(YA∣YC)P(YB∣YC)

上述成对、局部、全局的马尔可夫性的定义是等价的。
因子分解
最大团:若 C C C 是无向图 G G G 的一个团,并且不能再加入任何一个 G G G 的节点使其成为一个更大的团,则称此 C C C 为最大团。注意, G G G 中的最大团往往不止一个,并不是最大团中的最大团才叫做最大团。
因子分解:将概率无向图的联合概率分布 P ( Y ) P(Y) P(Y) 表示为其最大团上的随机变量的函数的乘积形式的操作,称为概率无向图模型的因子分解。由以下定理来保证:
Hammersley-Clifford 定理:概率无向图的联合概率分布 P ( Y ) P(Y) P(Y) 可以表示为如下形式:对于所有最大图 C C C , Y C Y_C YC 为某一最大图对应的随机变量序列,则:
P ( Y ) = 1 Z ∏ C Ψ C ( Y C ) P(Y)=\frac{1}{Z}\prod_{C}\Psi_C(Y_C) P(Y)=Z1C∏ΨC(YC)
其中 Z Z Z 是规范化因子,为:
Z = ∑ Y ∏ C Ψ C ( Y C ) Z=\sum\limits_{Y}\prod_{C}\Psi_C(Y_C) Z=Y∑C∏ΨC(YC)
规范化因子保证 P ( Y ) P(Y) P(Y) 构成一个概率分布(对 Y Y Y 的和为 1)。函数 Ψ C ( Y C ) \Psi_C(Y_C) ΨC(YC) 称为势函数(potential function),要求势函数严格正,通常定义为指数函数:
Ψ C ( Y C ) = e − E [ Y C ] \Psi_C(Y_C)=\mathrm{e}^{-E[Y_C]} ΨC(YC)=e−E[YC]
条件随机场
有 X X X 和 Y Y Y 两种随机变量, X X X 一般是给定的,而 Y Y Y 则是在给定 X X X 的条件下的输出(在十个词的句子词性标注的例子中, X X X 是词, Y Y Y 是词性)。若 Y Y Y 形成马尔可夫随机场,则条件概率分布 P ( X ∣ Y ) P(X|Y) P(X∣Y) 形成条件随机场。
这里主要介绍定义在线性链上的 CRF,可用于标注等问题。此时 Y Y Y 是输出变量,表示标记序列,也称为状态序列; X X X 是输入变量,表示要标注的观测序列。
- 学习时,利用训练集,通过极大似然估计或正则化的极大似然估计得到条件概率模型 P ^ ( Y ∣ X ) \hat P(Y|X) P^(Y∣X) ;
- 预测时,对于给定的输入序列 x x x ,求出条件概率 P ^ ( y ∣ x ) \hat P(y|x) P^(y∣x) 最大的输出序列 y ^ \hat y y^ ;
定义
条件随机场:设 X X X 与 Y Y Y 是随机变量, P ( Y ∣ X ) P(Y|X) P(Y∣X) 是在给定 X X X 的条件下 Y Y Y 的条件概率分布。若随机变量 Y Y Y 构成一个无向图 G = ( V , E ) G=(V,E) G=(V,E) 表示的马尔可夫随机场,即:
P ( Y v ∣ X , Y w , w ≠ v ) = P ( Y v ∣ X , Y w , w ∼ v ) P(Y_v|X,Y_w,w\not=v)=P(Y_v|X,Y_w,w\sim v) P(Yv∣X,Yw,w=v)=P(Yv∣X,Yw,w∼v)
对任意节点 v v v 成立,则条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X) 为条件随机场。其中 w ∼ v w\sim v w∼v 表示 G G G 中与节点 v v v 有边连接的节点。
本书考虑的无向图为线性链的情况,即:
G = ( V = { 1 , 2 , ⋯ , n } , E = { ( i , i + 1 ) ∣ i = 1 , 2 , ⋯ , n } ) G=(V=\set{1,2,\cdots,n},\,\,E=\set{(i,i+1)|i=1,2,\cdots,n}) G=(V={1,2,⋯,n},E={(i,i+1)∣i=1,2,⋯,n})
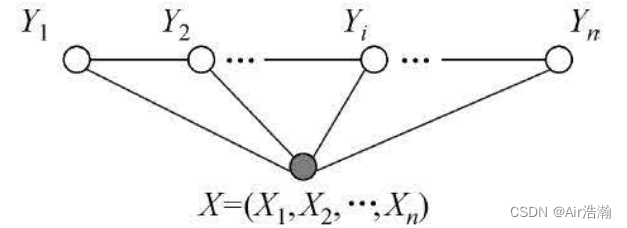
一般假设 X X X 和 Y Y Y 有相同的图结构, X = ( X 1 , X 2 , ⋯ , X n ) X=(X_1,X_2,\cdots,X_n) X=(X1,X2,⋯,Xn) , Y = ( Y 1 , Y 2 , ⋯ , Y n ) Y=(Y_1,Y_2,\cdots,Y_n) Y=(Y1,Y2,⋯,Yn) ,此时最大团为相邻两个节点的集合:
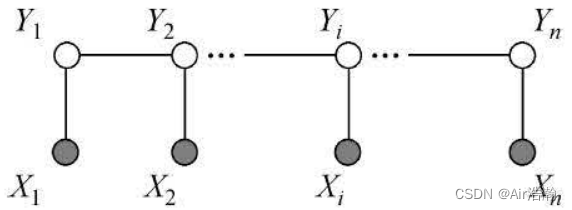
线性链条件随机场:设 X = ( X 1 , X 2 , ⋯ , X n ) X=(X_1,X_2,\cdots,X_n) X=(X1,X2,⋯,Xn) , Y = ( Y 1 , Y 2 , ⋯ , Y n ) Y=(Y_1,Y_2,\cdots,Y_n) Y=(Y1,Y2,⋯,Yn) 均为线性链表示的随机变量序列,若在给定随机变量序列 X X X 的条件下,随机变量序列 Y Y Y 的条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X) 构成条件随机场,即满足马尔可夫性:
P ( Y i ∣ X , Y 1 , ⋯ , Y i − 1 , Y i + 1 , ⋯ , Y n ) = P ( Y i ∣ X , Y i − 1 , Y i + 1 ) i = 1 , 2 , ⋯ , n ( i = 1 或 n 时只考虑单边 ) P(Y_i|X,Y_1,\cdots,Y_{i-1},Y_{i+1},\cdots,Y_n)=P(Y_i|X,Y_{i-1},Y_{i+1}) \\ i=1,2,\cdots,n \quad (i=1\text{ 或 }n\text{时只考虑单边}) P(Yi∣X,Y1,⋯,Yi−1,Yi+1,⋯,Yn)=P(Yi∣X,Yi−1,Yi+1)i=1,2,⋯,n(i=1 或 n时只考虑单边)
则称 P ( Y ∣ X ) P(Y|X) P(Y∣X) 为线性条件随机场。在标注问题中, X X X 表述输入观测序列, Y Y Y 表示对应的输出标记序列或状态序列。
参数化形式
线性链条件随机场是对数线性模型。逻辑回归和最大熵模型也是对数线性模型,参考之前的笔记,可以理解下面的公式和特征函数:
线性链条件随机场的参数化形式: P ( Y ∣ X ) P(Y|X) P(Y∣X) 具有以下形式:
P ( y ∣ x ) = 1 Z ( x ) exp ( ∑ i , k λ k t k ( y i − 1 , y i , x , i ) + ∑ i , l μ l s l ( y i , x , i ) ) P(y|x)=\frac{1}{Z(x)}\exp \left( \sum\limits_{i,k}\lambda_kt_k(y_{i-1},y_i,x,i)+\sum\limits_{i,l}\mu_ls_l(y_i,x,i) \right) P(y∣x)=Z(x)1exp i,k∑λktk(yi−1,yi,x,i)+i,l∑μlsl(yi,x,i)
其中:
Z ( x ) = ∑ y exp ( ∑ i , k λ k t k ( y i − 1 , y i , x , i ) + ∑ i , l μ l s l ( y i , x , i ) ) Z(x)=\sum\limits_{y}\exp\left( \sum\limits_{i,k}\lambda_kt_k(y_{i-1},y_i,x,i)+\sum\limits_{i,l}\mu_ls_l(y_i,x,i) \right) Z(x)=y∑exp i,k∑λktk(yi−1,yi,x,i)+i,l∑μlsl(yi,x,i)
- t k t_k tk 和 s l s_l sl 是特征函数, λ k \lambda_k λk 和 μ l \mu_l μl 是对应的权值; t k t_k tk 是定义在边上的特征,称为转移特征; s l s_l sl 是定义在节点上的特征,称为状态特征;
- Z ( x ) Z(x) Z(x) 是规范化因子,求和是在所有可能的输出序列上进行的;
- 特征函数参数中的 ’ i i i ’ 代表一个集合,即某个特征函数既可以描述某个位置的特征,也可以同时描述多个位置的特征;
- CRF 的参数即权重 w w w ;学习时,给定训练集和特征函数,我们要学习出最佳的权重 w w w ;
例:(从这个例子学习一下什么是特征)设有一个标注问题,输入观测序列为 X = ( X 1 , X 2 , X 3 ) X=(X_1,X_2,X_3) X=(X1,X2,X3) ,输出标记序列为 Y = ( Y 1 , Y 2 , Y 3 ) Y=(Y_1,Y_2,Y_3) Y=(Y1,Y2,Y3) ,其中 Y i ∈ Y = { 1 , 2 } Y_i\in \mathcal{Y}=\set{1,2} Yi∈Y={1,2} 。假设特征有:
t 1 = t 1 ( y i − 1 = 1 , y i = 2 , x , i ) , i = 2 , 3 , λ 1 = 1 t_1=t_1(y_{i-1}=1,y_i=2,x,i),\quad i=2,3, \quad \lambda_1=1 t1=t1(yi−1=1,yi=2,x,i),i=2,3,λ1=1
即:
t 1 ( y i − 1 , y i , x , i ) = { 1 , y i − 1 = 1 , y i = 2 , ∀ x , i = 2 , 3 0 , else t_1(y_{i-1},y_i,x,i)=\left\{ \begin{array}{ll} 1, & y_{i-1}=1,y_i=2,\forall x,i=2,3 \\ 0, & \text{else} \end{array} \right. t1(yi−1,yi,x,i)={1,0,yi−1=1,yi=2,∀x,i=2,3else
还有其他特征:
t 2 = t 2 ( y 1 = 1 , y 2 = 1 , x , 2 ) λ 2 = 0.6 t 3 = t 3 ( y 2 = 2 , y 3 = 1 , x , 3 ) λ 3 = 1 ⋯ s 1 = s 1 ( y 1 = 1 , x , 1 ) μ 1 = 1 s 2 = s 2 ( y i = 2 , x , i ) , i = 1 , 2 μ 2 = 0.5 ⋯ \begin{aligned} t_2=&\,t_2(y_1=1,y_2=1,x,2) & \lambda_2=0.6 \\ t_3=&\,t_3(y_2=2,y_3=1,x,3) & \lambda_3=1 \\ \cdots \\ s_1=&\,s_1(y_1=1,x,1) & \mu_1=1 \\ s_2=&\,s_2(y_i=2,x,i),i=1,2 & \mu_2=0.5 \\ \cdots \end{aligned} t2=t3=⋯s1=s2=⋯t2(y1=1,y2=1,x,2)t3(y2=2,y3=1,x,3)s1(y1=1,x,1)s2(yi=2,x,i),i=1,2λ2=0.6λ3=1μ1=1μ2=0.5
简化形式
我们简化特征函数,首先将转移特征和状态特征及其权值用统一的符号表示。设有 K 1 K_1 K1 个转移特征, K 2 K_2 K2 个状态特征, K = K 1 + K 2 K=K_1+K_2 K=K1+K2 ,记:
f k ( y i − 1 , y i , x , i ) = { t k ( y i − 1 , y i , x , i ) , k = 1 , 2 , ⋯ , K 1 s l ( y i , x , i ) , k = K 1 + l ; l = 1 , 2 , ⋯ , K 2 f_k(y_{i-1},y_{i},x,i)=\left\{ \begin{array}{ll} t_k(y_{i-1},y_i,x,i), & k=1,2,\cdots,K_1 \\ s_l(y_i,x,i), & k=K_1+l; \,l=1,2,\cdots,K_2 \end{array} \right. fk(yi−1,yi,x,i)={tk(yi−1,yi,x,i),sl(yi,x,i),k=1,2,⋯,K1k=K1+l;l=1,2,⋯,K2
然后,对特征在各个位置 i i i 求和(将特征函数的计算有效地归纳到整个序列上,从而减少了计算的复杂度):
f k ( y , x ) = ∑ i = 1 n f k ( y i − 1 , y i , x , i ) , k = 1 , 2 , ⋯ , K f_k(y,x)=\sum\limits_{i=1}^{n}f_k(y_{i-1},y_i,x,i), \quad k=1,2,\cdots,K fk(y,x)=i=1∑nfk(yi−1,yi,x,i),k=1,2,⋯,K
用 w k w_k wk 表示特征 f k ( y , x ) f_k(y,x) fk(y,x) 的权值,即:
w k = { λ k , k = 1 , 2 , ⋯ , K 1 μ l , k = K 1 + l ; l = 1 , 2 , ⋯ , K 2 w_k=\left\{ \begin{array}{ll} \lambda_k, & k=1,2,\cdots,K_1 \\ \mu_l, & k=K_1+l;\, l=1,2,\cdots,K_2 \end{array} \right. wk={λk,μl,k=1,2,⋯,K1k=K1+l;l=1,2,⋯,K2
于是,条件随机场可以表示为:
P ( y ∣ x ) = 1 Z ( x ) exp ∑ k = 1 K w k f k ( y , x ) Z ( x ) = ∑ y exp ∑ k = 1 K w k f k ( y , x ) \begin{aligned} P(y|x)=&\, \frac{1}{Z(x)}\exp\sum\limits_{k=1}^{K}w_kf_k(y,x) \\ Z(x)=&\, \sum\limits_{y}\exp\sum\limits_{k=1}^{K}w_kf_k(y,x) \\ \end{aligned} P(y∣x)=Z(x)=Z(x)1expk=1∑Kwkfk(y,x)y∑expk=1∑Kwkfk(y,x)
也可以写成向量内积的形式:
P w ( y ∣ x ) = exp ( w ⋅ F ( y , x ) ) Z w ( x ) Z ( x ) = ∑ y exp ( w ⋅ F ( y , x ) ) \begin{aligned} P_w(y|x)=&\, \frac{\exp{(w\cdot F(y,x))}}{Z_w(x)} \\ Z(x)=&\, \sum\limits_{y}\exp(w\cdot F(y,x)) \end{aligned} Pw(y∣x)=Z(x)=Zw(x)exp(w⋅F(y,x))y∑exp(w⋅F(y,x))
其中 w = ( w 1 , w 2 , ⋯ , w K ) T w=(w_1,w_2,\cdots,w_K)^\mathrm{T} w=(w1,w2,⋯,wK)T , F ( y , x ) = ( f 1 ( x , y ) , f 2 ( x , y ) , ⋯ , f K ( x , y ) ) T F(y,x)=(f_1(x,y),f_2(x,y),\cdots,f_K(x,y))^\mathrm{T} F(y,x)=(f1(x,y),f2(x,y),⋯,fK(x,y))T ;
矩阵形式
对每个标记序列,引入额外的起点和终点状态标记 y 0 = start y_0=\text{start} y0=start 和 y n + 1 = stop y_{n+1}=\text{stop} yn+1=stop ,有 start , stop ∈ Y \text{start},\,\text{stop}\in\mathcal{Y} start,stop∈Y;
对观测序列 x x x 的每一个位置 i = 1 , 2 , ⋯ , n + 1 i=1,2,\cdots,n+1 i=1,2,⋯,n+1 ,定义一个 m m m 阶矩阵随机变量:
M i ( x ) = [ M i ( y i − 1 , y i ∣ x ) ] M_i(x)=[M_i(y_{i-1},y_i|x)] Mi(x)=[Mi(yi−1,yi∣x)]
矩阵随机变量的元素为:(即所有特征函数在该位置的权重之和的指数)
M i ( y i − 1 , y i ∣ x ) = exp ( ∑ k = 1 K w k f k ( y i − 1 , y i , x , i ) ) M_i(y_{i-1},y_{i}|x)=\exp\left(\sum\limits_{k=1}^{K}w_kf_k(y_{i-1},y_i,x,i)\right) Mi(yi−1,yi∣x)=exp(k=1∑Kwkfk(yi−1,yi,x,i))
这里并未规范化,但是也可以看作是转移概率。因此给定观测序列 x x x ,相应标记序列 y y y 的非规范化概率可以通过矩阵的乘积表示;则条件概率为规范化后的矩阵乘积:
P w ( y ∣ x ) = 1 Z w ( x ) ∏ i = 1 n + 1 M i ( y i − 1 , y i ∣ x ) P_w(y|x)=\frac{1}{Z_w(x)}\prod_{i=1}^{n+1}M_{i}(y_{i-1},y_i|x) Pw(y∣x)=Zw(x)1i=1∏n+1Mi(yi−1,yi∣x)
其中, Z w ( x ) Z_w(x) Zw(x) 为规范化因子,是以 start 为起点 stop 为终点通过状态的所有路径 y 1 y 2 ⋯ y n y_1y_2\cdots y_n y1y2⋯yn 的非规范化概率 ∏ i = 1 n + 1 M i ( y i − 1 , y i ∣ x ) \prod\limits_{i=1}^{n+1}M_{i}(y_{i-1},y_i|x) i=1∏n+1Mi(yi−1,yi∣x) 之和,即所有矩阵的乘积的第 start \text{start} start 行 stop \text{stop} stop 列元素:
Z w ( x ) = [ M 1 ( x ) M 2 ( x ) ⋯ M n + 1 ( x ) ] start,stop Z_w(x)=[M_1(x)M_2(x)\cdots M_{n+1}(x)]_{\text{start,stop}} Zw(x)=[M1(x)M2(x)⋯Mn+1(x)]start,stop
概率预测问题
CRF 的概率预测问题即给定 P ( Y ∣ X ) P(Y|X) P(Y∣X) ,输入序列 x x x 和输出序列 y y y ,计算条件概率 P ( Y i = y i ∣ x ) P(Y_i=y_i|x) P(Yi=yi∣x) , P ( Y i − 1 = y i − 1 , Y i = y i ∣ x ) P(Y_{i-1}=y_{i-1},Y_{i}=y_i|x) P(Yi−1=yi−1,Yi=yi∣x) 以及特征函数的数学期望的问题。计算方法和 HMM 类似,也需要前向和后向变量,递归地求解以上问题。
概率预测问题使用矩阵形式的 CRF;
前向-后向算法
对每个下标 i = 0 , 1 , ⋯ , n + 1 i=0,1,\cdots,n+1 i=0,1,⋯,n+1 ,定义前向向量 α i ( x ) \alpha_i(x) αi(x) ;每个 α i ( x ) \alpha_i(x) αi(x) 都是一个向量,其下标分别对应 Y Y Y 某个可能的取值; Y Y Y 的取值有 m m m 个,因此 α i ( x ) \alpha_i(x) αi(x) 是 m m m 维列向量。其中:
α 0 ( y ∣ x ) = { 1 , y = start 0 , else \alpha_0(y|x)=\left\{ \begin{array}{ll} 1, & y=\text{start} \\ 0, & \text{else} \end{array} \right. α0(y∣x)={1,0,y=startelse
递推公式为:(因为定义 M M M 行下标为前一状态,列下标为下一状态,所以 α \alpha α 就变得麻烦,要取转置)
α i T ( x ) = α i − 1 T ( x ) M i ( x ) \alpha^{T}_i(x)=\alpha^{T}_{i-1}(x)M_i(x) αiT(x)=αi−1T(x)Mi(x)
α i ( y i ∣ x ) \alpha_{i}(y_i|x) αi(yi∣x) 表示到位置 i i i 的标记为 y i y_i yi 的非规范化概率。
同样地,定义后向向量 β i ( x ) \beta_i(x) βi(x) :
β n + 1 ( y ∣ x ) = { 1 , y = stop 0 , else \beta_{n+1}(y|x)=\left\{ \begin{array}{ll} 1, & y=\text{stop} \\ 0, & \text{else} \end{array} \right. βn+1(y∣x)={1,0,y=stopelse
递推公式为:
β i ( x ) = M i + 1 ( x ) β i + 1 ( x ) \beta_i(x)=M_{i+1}(x)\beta_{i+1}(x) βi(x)=Mi+1(x)βi+1(x)
β i ( y i ∣ x ) \beta_{i}(y_i|x) βi(yi∣x) 表示从后往前到位置 i i i 的标记为 y i y_i yi 的非规范化概率。
概率的计算
经过点的概率:在位置 i i i 为标记 y i y_i yi 的条件概率为:
P ( Y i = y i ∣ x ) = α i T ( y i ∣ x ) β i ( y i ∣ x ) Z ( x ) P(Y_i=y_i|x)=\frac{\alpha_i^T(y_i|x)\beta_{i}(y_i|x)}{Z(x)} P(Yi=yi∣x)=Z(x)αiT(yi∣x)βi(yi∣x)
经过边的概率:在位置 i − 1 i-1 i−1 和位置 i i i 是标记 y i − 1 y_{i-1} yi−1 和 y i y_i yi 的概率为:
P ( Y i − 1 = y i − 1 , Y i = y i ∣ x ) = α i = 1 T ( y i − 1 ∣ x ) M ( y i − 1 , y i ∣ x ) β i ( y i ∣ x ) Z ( x ) P(Y_{i-1}=y_{i-1},Y_i=y_i|x)=\frac{\alpha_{i=1}^{T}(y_{i-1}|x)M(y_{i-1},y_{i}|x)\beta_i(y_i|x)}{Z(x)} P(Yi−1=yi−1,Yi=yi∣x)=Z(x)αi=1T(yi−1∣x)M(yi−1,yi∣x)βi(yi∣x)
其中规范因子可以用新的方法计算:
Z ( x ) = α n T ( x ) 1 = 1 β 1 ( x ) Z(x)=\alpha_n^T(x)\bold{1}=\bold{1}\beta_{1(x)} Z(x)=αnT(x)1=1β1(x)
期望值的计算
特征函数 f k f_k fk 关于条件分布 P ( Y ∣ X ) P(Y|X) P(Y∣X) 的数学期望是(相当于给定 x x x 的期望):
$$
\begin{aligned}
E_{P(Y|X)}[f_k]
=&,\sum\limits_{y}P(y|x)f_k(y,x) \
=&,\sum\limits_{i=1}{n+1}\sum\limits_{y_{i-1},y_i}f_k(y_{i-1},y_i,x,i)\frac{\alpha_{i=1}{T}(y_{i-1}|x)M(y_{i-1},y_{i}|x)\beta_i(y_i|x)}{Z(x)} \
&, k=1,2,\cdots,K
\end{aligned}
KaTeX parse error: Can't use function '$' in math mode at position 10: 假设经验分布为 $̲\tilde P(X)$ ,特…
\begin{aligned}
E_{P(X,Y)}[f_k]
=&,\sum\limits_{x,y}P(x,y)\sum\limits_{i=1}^{n+1}f_k(y_{i-1},y_i,x,i) \
=&, \sum\limits_{x}\tilde P(x) \sum\limits_{y}P(y|x)\sum\limits_{i=1}^{n+1}f_k(y_{i-1},y_i,x,i) \
=&,\sum\limits_{x}\tilde P(x)
\sum\limits_{i=1}{n+1}\sum\limits_{y_{i-1},y_i}f_k(y_{i-1},y_i,x,i)\frac{\alpha_{i=1}{T}(y_{i-1}|x)M(y_{i-1},y_{i}|x)\beta_i(y_i|x)}{Z(x)} \
&, k=1,2,\cdots,K
\end{aligned}
$$
这两个期望是 ∈ [ 0 , 1 ] \in[0,1] ∈[0,1] 的,因为如果该特征函数的 i i i 有多个取值,则需要对所有位置求平均。
特征函数的期望是用在 CRF 的学习问题中的,因为学习的目的是要让学习到的模型尽可能反映训练集的特征,二者对于特征函数的期望要尽可能相等。
学习问题
CRF 实际上是定义在时序数据上的对数线性模型,其学习问题主要是学习 P ( y ∣ x ) P(y|x) P(y∣x) ,学习方法常有极大似然估计和正则化的极大似然估计。具体的优化算法有 IIS、梯度下降法及拟牛顿法。
学习问题使用参数形式的 CRF(因为就是要学习参数)
改进的迭代尺度法
IIS 可以理解为,不断更新参数,从而使得学习到的模型尽可能反映数据集的特征,即二者特征的总数尽可能相等。
CRF 的 IIS 推导:已知训练集,则可知经验概率分布 P ~ ( X , Y ) \tilde P(X,Y) P~(X,Y) ; IIS 通过极大化训练数据的对数似然函数来求模型参数。训练数据的对数似然函数为(该似然函数的推导过程可以参考最大熵的笔记):
L ( w ) = L P ~ ( P w ) = log ∏ x , y P w ( y ∣ x ) P ~ ( x , y ) = ∑ x , y P ~ ( x , y ) log P w ( y ∣ x ) L(w)=L_{\tilde P}(P_w)=\log \prod_{x,y}P_w(y|x)^{\tilde P(x,y)}=\sum\limits_{x,y}\tilde P(x,y)\log P_w(y|x) L(w)=LP~(Pw)=logx,y∏Pw(y∣x)P~(x,y)=x,y∑P~(x,y)logPw(y∣x)
带入 CRF 的参数形式可以得到:
$$
\begin{aligned}
L(w)
=&,\sum\limits_{x,y}\tilde P(x,y)\log P_w(y|x) \
=&,\sum\limits_{x,y} \left[ \tilde P(x,y)\sum\limits_{k=1}^{K}w_kf_k(y,x)
-
\tilde P(x,y)\log Z_w(x) \right] \
=&, \frac{1}{N} \left( \sum\limits_{j=1}{N}\sum\limits_{k=1}{K}w_kf_k(y_j,x_j)-\sum\limits_{j=1}^{N}\log Z_w(x_j) \right)
\end{aligned}
$$ -
第三个等号中,考虑以下经验概率分布的定义: P ~ ( x , y ) = v ( x , y ) N \tilde P(x,y)=\frac{v(x,y)}{N} P~(x,y)=Nv(x,y) ,即 ( x , y ) (x,y) (x,y) 出现的频数,所以我们直接将频数拆开;
训练集大小 N N N 与优化无关,因此直接将对数似然函数写作:
L ( w ) = ∑ j = 1 N ∑ k = 1 K w k f k ( y j , x j ) − ∑ j = 1 N log Z w ( x j ) L(w)=\sum\limits_{j=1}^{N}\sum\limits_{k=1}^{K}w_kf_k(y_j,x_j)-\sum\limits_{j=1}^{N}\log Z_w(x_j) L(w)=j=1∑Nk=1∑Kwkfk(yj,xj)−j=1∑NlogZw(xj)
IIS 通过迭代的方法不断优化对数似然函数该变量的下界,达到极大化对数似然函数的目的。假设模型的当前参数为 w = ( w 1 , w 2 . ⋯ , w K ) T w=(w_1,w_2.\cdots,w_K)^T w=(w1,w2.⋯,wK)T ,增量为 δ = ( δ 1 , δ 2 , ⋯ , δ K ) T \delta=(\delta_1,\delta_2,\cdots,\delta_K)^T δ=(δ1,δ2,⋯,δK)T ,更新参数向量为:
w + δ = ( w 1 + δ 1 , w 2 + δ 2 , ⋯ , w K + δ K ) w+\delta=(w_1+\delta_1,w_2+\delta_2,\cdots,w_K+\delta_K) w+δ=(w1+δ1,w2+δ2,⋯,wK+δK)
IIS 依次求解两个方程得到 δ \delta δ (推导过程参考逻辑回归和最大熵的笔记);
转移特征 t k t_k tk 在经验概率下的期望为:
E P ~ [ t k ] = ∑ x , y P ~ ( x , y ) ∑ i = 1 n + 1 t k ( y i − 1 , y i , x , i ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) ∑ i = 1 n + 1 t k ( y i − 1 , y i , x , i ) exp ( δ k T ( x , y ) ) k = 1 , 2 , ⋯ , K 1 \begin{aligned} E_{\tilde P}[t_k] =&\, \sum\limits_{x,y}\tilde P(x,y)\sum\limits_{i=1}^{n+1}t_k(y_{i-1},y_i,x,i) \\ =&\, \sum\limits_{x,y}\tilde P(x)P(y|x)\sum\limits_{i=1}^{n+1}t_k(y_{i-1},y_i,x,i) \exp(\delta_kT(x,y)) \\ &\, k=1,2,\cdots,K_1 \end{aligned} EP~[tk]==x,y∑P~(x,y)i=1∑n+1tk(yi−1,yi,x,i)x,y∑P~(x)P(y∣x)i=1∑n+1tk(yi−1,yi,x,i)exp(δkT(x,y))k=1,2,⋯,K1
状态特征 s l s_l sl 在经验概率下的期望为:
E P ~ [ s l ] = ∑ x , y P ~ ( x , y ) ∑ i = 1 n + 1 s l ( y i , x , i ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) ∑ i = 1 n + 1 s l ( y i , x , i ) exp ( δ K 1 + l T ( x , y ) ) l = 1 , 2 , ⋯ , K 2 \begin{aligned} E_{\tilde P}[s_l] =&\, \sum\limits_{x,y}\tilde P(x,y)\sum\limits_{i=1}^{n+1}s_l(y_i,x,i) \\ =&\, \sum\limits_{x,y}\tilde P(x)P(y|x)\sum\limits_{i=1}^{n+1}s_l(y_i,x,i) \exp(\delta_{K_1+l}T(x,y)) \\ &\, l=1,2,\cdots,K_2 \end{aligned} EP~[sl]==x,y∑P~(x,y)i=1∑n+1sl(yi,x,i)x,y∑P~(x)P(y∣x)i=1∑n+1sl(yi,x,i)exp(δK1+lT(x,y))l=1,2,⋯,K2
这里, T ( x , y ) T(x,y) T(x,y) 是在数据 ( x , y ) (x,y) (x,y) 中出现所有特征的总和:
T ( x , y ) = ∑ k f k ( y , x ) = ∑ k = 1 K ∑ i = 1 n + 1 f k ( y i − 1 y i , x , i ) T(x,y)=\sum\limits_{k}f_k(y,x)=\sum\limits_{k=1}^{K}\sum\limits_{i=1}^{n+1}f_k(y_{i-1}y_i,x,i) T(x,y)=k∑fk(y,x)=k=1∑Ki=1∑n+1fk(yi−1yi,x,i)
算法:条件随机场模型学习的改进的迭代尺度法
- 输入:特征函数 t 1 , t 2 , ⋯ , t K 1 t_1,\,t_2,\,\cdots,\,t_{K_1} t1,t2,⋯,tK1 , s 1 , s 2 , ⋯ , s K 2 s_1,\,s_2,\,\cdots,\,s_{K_2} s1,s2,⋯,sK2 ;训练集 T T T 和对应的经验分布 P ~ ( x , y ) \tilde P(x,y) P~(x,y)
- 输出:参数估计 w ^ \hat w w^ ;模型 P w ^ P_{\hat w} Pw^ ;
-
对所有 k ∈ { 1 , 2 , ⋯ , K } k\in \set{1,2,\cdots,K} k∈{1,2,⋯,K} ,取初值为 w k = 0 w_k=0 wk=0 ;
-
求出 δ k \delta_k δk , k = 1 , 2 , ⋯ , K k=1,2,\cdots,K k=1,2,⋯,K :
- 当 1 ≤ k ≤ K 1 1\leq k \leq K_1 1≤k≤K1 ,即对于转移特征的参数变化量, δ k \delta_k δk 为以下方程的解:
∑ x , y P ~ ( x ) P ( y ∣ x ) ∑ i = 1 n + 1 t k ( y i − 1 , y i , x , i ) exp ( δ k T ( x , y ) ) = E P ~ [ t k ] \sum\limits_{x,y}\tilde P(x)P(y|x)\sum\limits_{i=1}^{n+1}t_k(y_{i-1},y_i,x,i)\exp (\delta_kT(x,y))=E_{\tilde P}[t_k] x,y∑P~(x)P(y∣x)i=1∑n+1tk(yi−1,yi,x,i)exp(δkT(x,y))=EP~[tk]
- 当 k = K 1 + l , 1 ≤ l ≤ K 2 k=K_1+l,\,1\leq l \leq K_2 k=K1+l,1≤l≤K2 ,即对于状态特征的参数变化量, δ K 1 + l \delta_{K_1+l} δK1+l 为以下方程的解:
∑ x , y P ~ ( x ) P ( y ∣ x ) ∑ i = 1 n + 1 s l ( y i , x , i ) exp ( δ K 1 + l T ( x , y ) ) = E P ~ [ s k ] \sum\limits_{x,y}\tilde P(x)P(y|x)\sum\limits_{i=1}^{n+1}s_l(y_i,x,i)\exp (\delta_{K_1+l}T(x,y))=E_{\tilde P}[s_k] x,y∑P~(x)P(y∣x)i=1∑n+1sl(yi,x,i)exp(δK1+lT(x,y))=EP~[sk]
-
更新 w k w_k wk 值: w k ← w k + δ k w_k \leftarrow w_k+\delta_k wk←wk+δk ;
-
如果不是所有的 w k w_k wk 收敛,则重复算法;
算法 S:由于 T ( x , y ) T(x,y) T(x,y) 表示某个数据 ( x , y ) (x,y) (x,y) 中的特征总数,难以计算,我们可以定义一个松弛特征 S S S , S S S 是一个足够大的常数,使得:
S ≥ max x , y ∑ i = 1 n + 1 ∑ k = 1 K f k ( y i − 1 , y i , x , i ) S \geq \max_{x,y}\sum\limits_{i=1}^{n+1}\sum\limits_{k=1}^{K}f_k(y_{i-1},y_i,x,i) S≥x,ymaxi=1∑n+1k=1∑Kfk(yi−1,yi,x,i)
则每次更新参数时可以将 S S S 作为特征总数。
此时,对于转移特征 t k t_k tk , δ k \delta_k δk 的更新方程为:
∑ x , y P ~ ( x ) P ( y ∣ x ) ∑ i = 1 n + 1 t k ( y i − 1 , y i , x , i ) exp ( δ k S ) = E P ~ [ t k ] ⇒ δ k = 1 S log E P ~ [ t k ] E P [ t k ] \sum\limits_{x,y}\tilde P(x)P(y|x)\sum\limits_{i=1}^{n+1}t_k(y_{i-1},y_i,x,i)\exp (\delta_kS)=E_{\tilde P}[t_k] \\ \Rightarrow \delta_k=\frac{1}{S}\log \frac{E_{\tilde P}[t_k]}{E_P[t_k]} x,y∑P~(x)P(y∣x)i=1∑n+1tk(yi−1,yi,x,i)exp(δkS)=EP~[tk]⇒δk=S1logEP[tk]EP~[tk]
对于状态特征 s l s_l sl , δ k \delta_k δk 的更新方程为:
∑ x , y P ~ ( x ) P ( y ∣ x ) ∑ i = 1 n + 1 s l ( y i , x , i ) exp ( δ k S ) = E P ~ [ s l ] ⇒ δ k = 1 S log E P ~ [ s l ] E P [ s l ] \sum\limits_{x,y}\tilde P(x)P(y|x)\sum\limits_{i=1}^{n+1}s_l(y_i,x,i)\exp (\delta_kS)=E_{\tilde P}[s_l] \\ \Rightarrow \delta_k=\frac{1}{S}\log \frac{E_{\tilde P}[s_l]}{E_P[s_l]} x,y∑P~(x)P(y∣x)i=1∑n+1sl(yi,x,i)exp(δkS)=EP~[sl]⇒δk=S1logEP[sl]EP~[sl]
其中 E P [ t k ] E_P[t_k] EP[tk] 和 E P [ s l ] E_P[s_l] EP[sl] 的计算参考前面的概率计算问题。
算法 T :算法 S 中一次性选了一个很大的 S,会使得每次迭代时 δ \delta δ 都变大,算法收敛速度则会变慢。算法 T 则在 T ( x , y ) T(x,y) T(x,y) 和 S S S 中折中选择了一个值:
T ( x ) = max y T ( x , y ) T(x)=\max_{y}T(x,y) T(x)=ymaxT(x,y)
(后面什么 T ( x ) = t T(x)=t T(x)=t 的没看懂是什么意思,也不知道为什么说 T ( x ) T(x) T(x) 很容易计算)
拟牛顿法
CRF 的拟牛顿法推导:参考牛顿法和拟牛顿法的笔记。对于 CRF 的参数形式:(我们这里假设特征有 n n n 个,虽然前面都是假设特征有 K K K 个,但是牛顿法中 k k k 往往代表迭代的次数):
P ( y ∣ x ) = exp ∑ i = 1 n w i f i ( y , x ) ∑ y exp ∑ i = 1 n w i f i ( y , x ) \begin{aligned} P(y|x)=&\, \frac{\exp\sum\limits_{i=1}^{n}w_if_i(y,x)} {\sum\limits_{y}\exp\sum\limits_{i=1}^{n}w_if_i(y,x)} \\ \end{aligned} P(y∣x)=y∑expi=1∑nwifi(y,x)expi=1∑nwifi(y,x)
目标函数为对数似然函数,但牛顿法求的是极小值问题,因此取个负号。学习的优化目标函数是:
min w ∈ R n f ( w ) = − L ( w ) = ∑ x P ~ ( x ) log ∑ y exp ( ∑ i = 1 n w i f i ( x , y ) ) − ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) \begin{aligned} \min\limits_{w\in\R^n} f(w)=&\,-L(w) \\ =&\,\sum\limits_{x}\tilde P(x)\log \sum\limits_{y}\exp \left( \sum\limits_{i=1}^{n}w_if_i(x,y)\right)-\sum\limits_{x,y}\tilde P(x,y)\sum\limits_{i=1}^{n}w_if_i(x,y) \end{aligned} w∈Rnminf(w)==−L(w)x∑P~(x)logy∑exp(i=1∑nwifi(x,y))−x,y∑P~(x,y)i=1∑nwifi(x,y)
其梯度函数为:
g ( w i ) = ∑ x , y P ~ ( x ) P w ( y ∣ x ) f i ( x , y ) − E P ~ ( f i ) g(w_i)=\sum\limits_{x,y}\tilde P(x)P_w(y|x)f_i(x,y)-E_{\tilde P}(f_i) g(wi)=x,y∑P~(x)Pw(y∣x)fi(x,y)−EP~(fi)
这个梯度其实就是模型的概率分布下和经验概率分布下第 i i i 个特征的期望之差;当梯度足够小时,我们就认为模型学习到了训练数据的特征。
算法:条件随机场模型学习的 BFGS 算法
- 输入:特征函数 f 1 f_1 f1 , f 2 f_2 f2 , ⋯ \cdots ⋯ , f n f_n fn ,经验分布 P ~ ( X , Y ) \tilde P(X,Y) P~(X,Y) ,精度 ε \varepsilon ε;
- 输出:最优参数值 w ^ \hat w w^ ,最优模型 P w ^ ( Y ∣ X ) P_{\hat w}(Y|X) Pw^(Y∣X) ;
- 选定初始点 w ( 0 ) w^{(0)} w(0) ,取 B 0 B_0 B0 为正定矩阵,置 k = 0 k=0 k=0 ;
- 计算 g k = g ( w ( k ) ) g_k=g(w^{(k)}) gk=g(w(k)) ,若 ∥ g k ∥ < ε \|g_k\|\lt \varepsilon ∥gk∥<ε ,则停止计算,返回参数值 w ^ = w ( k ) \hat w=w^{(k)} w^=w(k) 和最优模型 P w ^ ( Y ∣ X ) P_{\hat w}(Y|X) Pw^(Y∣X) ;
- 由 B k p k = − g k B_kp_k=-g_k Bkpk=−gk 求得 p k p_k pk ;
- 一维搜索:求 λ k \lambda_k λk 使得:
f ( w ( k ) + λ k p k ) = min λ ≥ 0 f ( w ( k ) + λ p k ) f(w^{(k)}+\lambda_kp_k)=\min\limits_{\lambda \geq 0} f(w^{(k)}+\lambda p_k) f(w(k)+λkpk)=λ≥0minf(w(k)+λpk)
- 更新 w ( k + 1 ) = w ( k ) + λ k p k w^{(k+1)}=w^{(k)}+\lambda_kp_k w(k+1)=w(k)+λkpk ;更新 B k + 1 B_{k+1} Bk+1 :
B k + 1 = B k + y k y k T y k T δ k − B k δ k δ k T B k δ k T B k δ k B_{k+1}=B_k+\frac{y_ky_k^{\mathrm{T}}}{y_k^{\mathrm{T}}\delta_k}-\frac{B_k\delta_k\delta_k^{\mathrm{T}}B_k}{\delta_k^{\mathrm{T}}B_k\delta_k} Bk+1=Bk+ykTδkykykT−δkTBkδkBkδkδkTBk
- 置 k = k + 1 k=k+1 k=k+1 ,跳转至 2;
解码问题
解码问题也叫预测问题,是给定条件随机场 P ( Y ∣ X ) P(Y|X) P(Y∣X) 和输入序列 (观测序列) x x x,求条件概率最大的输出序列(标记序列) y ∗ y^\ast y∗ ,即对序列进行标注。CRF 的解码问题也是使用维特比算法,可以参考HMM 的笔记。
CRF 的 Viterbi 算法推导:有:
y ∗ = arg max y P w ( y ∣ x ) = arg max y exp ( w ⋅ F ( y , x ) ) Z w ( x ) = arg max y w ⋅ F ( y , x ) \begin{aligned} y^\ast =&\, \arg\max_yP_w(y|x) \\ =&\, \arg\max_y \frac{\exp(w\cdot F(y,x))}{Z_w(x)} \\ =&\, \arg\max_yw\cdot F(y,x) \end{aligned} y∗===argymaxPw(y∣x)argymaxZw(x)exp(w⋅F(y,x))argymaxw⋅F(y,x)
因此 CRF 的的解码问题变为求非规范化概率最大的最优路径问题。此时只需要计算非规范化概率,而不必计算概率,可以大大提高效率。
首先求出下标 1 1 1 的各个标记 j = 1 , 2 , ⋯ , m j=1,2,\cdots,m j=1,2,⋯,m 的非规范化概率:
δ 1 ( j ) = w ⋅ F 1 ( y 0 = start , y 1 = j , x ) , j = 1 , 2 , ⋯ , m \delta_1(j)=w \cdot F_1(y_0=\text{start},\,y_1=j,x),\quad j=1,2,\cdots,m δ1(j)=w⋅F1(y0=start,y1=j,x),j=1,2,⋯,m
递推得到各个位置 i = 2 , 3 , ⋯ n i=2,3,\cdots n i=2,3,⋯n 的各个标记 l = 1 , 2 , ⋯ , m l=1,2,\cdots,m l=1,2,⋯,m 的非规范化概率的最大值,同时记录路径:
δ i ( l ) = max 1 ≤ j ≤ m { δ i − 1 ( j ) + w ⋅ F i ( y i − 1 = j , y i = l , x ) } , l = 1 , 2 , ⋯ , m Ψ i ( l ) = arg max 1 ≤ j ≤ m { δ i − 1 ( j ) + w ⋅ F i ( y i − 1 = j , y i = l , x ) } , l = 1 , 2 , ⋯ , m \delta_i(l)=\max\limits_{1\leq j\leq m} \set{\delta_{i-1}(j)+w\cdot F_i(y_{i-1}=j,y_i=l,x)},\quad l=1,2,\cdots,m \\ \Psi_i(l)=\arg\max\limits_{1\leq j\leq m} \set{\delta_{i-1}(j)+w\cdot F_i(y_{i-1}=j,y_i=l,x)},\quad l=1,2,\cdots,m δi(l)=1≤j≤mmax{δi−1(j)+w⋅Fi(yi−1=j,yi=l,x)},l=1,2,⋯,mΨi(l)=arg1≤j≤mmax{δi−1(j)+w⋅Fi(yi−1=j,yi=l,x)},l=1,2,⋯,m
递推到 i = n i=n i=n 时,得到非规范化概率的最大值:
max y ( w ⋅ F ( y , x ) ) = max 1 ≤ j ≤ m δ n ( j ) \max_y (w\cdot F(y,x))=\max\limits_{1\leq j\leq m}\delta_n(j) ymax(w⋅F(y,x))=1≤j≤mmaxδn(j)
以及最优路径的终点:
y n ∗ = arg max 1 ≤ j ≤ m δ n ( j ) y^\ast_n=\arg\max_{1\leq j\leq m}\delta_n(j) yn∗=arg1≤j≤mmaxδn(j)
并回溯得到最优路径:
y i ∗ = Ψ i + 1 ( y i + 1 ∗ ) , i = n − 1 , n − 2 , ⋯ , 1 y^\ast_i=\Psi_{i+1}(y^\ast_{i+1}),\quad i=n-1,n-2,\cdots,1 yi∗=Ψi+1(yi+1∗),i=n−1,n−2,⋯,1
求得最优路径 y ∗ = ( y 1 ∗ , y 2 ∗ , ⋯ , y n ∗ ) T y^\ast=(y^\ast_1,y^\ast_2,\cdots,y_n^\ast)^\mathrm{T} y∗=(y1∗,y2∗,⋯,yn∗)T ;
算法:条件随机场预测的维特比算法
- 输入:模型特征向量 F ( y , x ) F(y,x) F(y,x) 和权值向量 w w w ,观测序列 x = ( x 1 , x 2 , ⋯ , x n ) x=(x_1,x_2,\cdots,x_n) x=(x1,x2,⋯,xn) ;
- 输出: y ∗ = ( y 1 ∗ , y 2 ∗ , ⋯ , y n ∗ ) T y^\ast=(y^\ast_1,y^\ast_2,\cdots,y_n^\ast)^\mathrm{T} y∗=(y1∗,y2∗,⋯,yn∗)T ;
- 初始化:
δ 1 ( j ) = w ⋅ F 1 ( y 0 = start , y 1 = j , x ) , j = 1 , 2 , ⋯ , m \delta_1(j)=w \cdot F_1(y_0=\text{start},\,y_1=j,x),\quad j=1,2,\cdots,m δ1(j)=w⋅F1(y0=start,y1=j,x),j=1,2,⋯,m
- 递推:对 i = 2 , 3 , ⋯ , n i=2,3,\cdots,n i=2,3,⋯,n :
δ i ( l ) = max 1 ≤ j ≤ m { δ i − 1 ( j ) + w ⋅ F i ( y i − 1 = j , y i = l , x ) } , l = 1 , 2 , ⋯ , m Ψ i ( l ) = arg max 1 ≤ j ≤ m { δ i − 1 ( j ) + w ⋅ F i ( y i − 1 = j , y i = l , x ) } , l = 1 , 2 , ⋯ , m \delta_i(l)=\max\limits_{1\leq j\leq m} \set{\delta_{i-1}(j)+w\cdot F_i(y_{i-1}=j,y_i=l,x)},\quad l=1,2,\cdots,m \\ \Psi_i(l)=\arg\max\limits_{1\leq j\leq m} \set{\delta_{i-1}(j)+w\cdot F_i(y_{i-1}=j,y_i=l,x)},\quad l=1,2,\cdots,m δi(l)=1≤j≤mmax{δi−1(j)+w⋅Fi(yi−1=j,yi=l,x)},l=1,2,⋯,mΨi(l)=arg1≤j≤mmax{δi−1(j)+w⋅Fi(yi−1=j,yi=l,x)},l=1,2,⋯,m
- 终止:
max y ( w ⋅ F ( y , x ) ) = max 1 ≤ j ≤ m δ n ( j ) y n ∗ = arg max 1 ≤ j ≤ m δ n ( j ) \max_y (w\cdot F(y,x))=\max\limits_{1\leq j\leq m}\delta_n(j) \\ y^\ast_n=\arg\max_{1\leq j\leq m}\delta_n(j) ymax(w⋅F(y,x))=1≤j≤mmaxδn(j)yn∗=arg1≤j≤mmaxδn(j)
- 返回路径:
y i ∗ = Ψ i + 1 ( y i + 1 ∗ ) , i = n − 1 , n − 2 , ⋯ , 1 y^\ast_i=\Psi_{i+1}(y^\ast_{i+1}),\quad i=n-1,n-2,\cdots,1 yi∗=Ψi+1(yi+1∗),i=n−1,n−2,⋯,1
求得最优路径 y ∗ = ( y 1 ∗ , y 2 ∗ , ⋯ , y n ∗ ) T y^\ast=(y^\ast_1,y^\ast_2,\cdots,y_n^\ast)^\mathrm{T} y∗=(y1∗,y2∗,⋯,yn∗)T ;
例:设有一个标注问题,输入观测序列为 X = ( X 1 , X 2 , X 3 ) X=(X_1,X_2,X_3) X=(X1,X2,X3) ,输出标记序列为 Y = ( Y 1 , Y 2 , Y 3 ) Y=(Y_1,Y_2,Y_3) Y=(Y1,Y2,Y3) ,其中 Y i ∈ Y = { 1 , 2 } Y_i\in \mathcal{Y}=\set{1,2} Yi∈Y={1,2} 。假设特征有:
t 1 = t 1 ( y i − 1 = 1 , y i = 2 , x , i ) , i = 2 , 3 λ 1 = 1 t 2 = t 2 ( y 1 = 1 , y 2 = 1 , x , 2 ) λ 2 = 0.6 t 3 = t 3 ( y 2 = 2 , y 3 = 1 , x , 3 ) λ 3 = 1 t 4 = t 4 ( y 1 = 2 , y 2 = 1 , x , 2 ) λ 4 = 1 t 5 = t 5 ( y 2 = 2 , y 3 = 2 , x , 3 ) λ 3 = 0.2 s 1 = s 1 ( y 1 = 1 , x , 1 ) μ 1 = 1 s 2 = s 2 ( y i = 2 , x , i ) , i = 1 , 2 μ 2 = 0.5 s 3 = s 3 ( y i = 1 , x , i ) , i = 2 , 3 μ 3 = 0.8 s 4 = s 4 ( y 3 = 2 , x , 3 ) μ 4 = 0.5 \begin{aligned} t_1=&\,t_1(y_{i-1}=1,y_i=2,x,i),i=2,3 & \lambda_1=1 \\ t_2=&\,t_2(y_1=1,y_2=1,x,2) & \lambda_2=0.6 \\ t_3=&\,t_3(y_2=2,y_3=1,x,3) & \lambda_3=1 \\ t_4=&\,t_4(y_1=2,y_2=1,x,2) & \lambda_4=1 \\ t_5=&\,t_5(y_2=2,y_3=2,x,3) & \lambda_3=0.2 \\ s_1=&\,s_1(y_1=1,x,1) & \mu_1=1 \\ s_2=&\,s_2(y_i=2,x,i),i=1,2 & \mu_2=0.5 \\ s_3=&\,s_3(y_i=1,x,i),i=2,3 & \mu_3=0.8 \\ s_4=&\,s_4(y_3=2,x,3) & \mu_4=0.5 \\ \end{aligned} t1=t2=t3=t4=t5=s1=s2=s3=s4=t1(yi−1=1,yi=2,x,i),i=2,3t2(y1=1,y2=1,x,2)t3(y2=2,y3=1,x,3)t4(y1=2,y2=1,x,2)t5(y2=2,y3=2,x,3)s1(y1=1,x,1)s2(yi=2,x,i),i=1,2s3(yi=1,x,i),i=2,3s4(y3=2,x,3)λ1=1λ2=0.6λ3=1λ4=1λ3=0.2μ1=1μ2=0.5μ3=0.8μ4=0.5
这里给出的特征对 x x x 都没什么要求,因此不论观测序列是什么,它们都对应同一个最大概率的标记序列 y ∗ = ( y 1 ∗ , y 2 ∗ , y 3 ∗ ) y^\ast=(y_1^\ast,y_2^\ast,y_3^\ast) y∗=(y1∗,y2∗,y3∗) ;
Y δ 1 , Ψ 1 δ 2 , Ψ 2 δ 3 , Ψ 3 1 1 , / 2.4 , 1 4.3 , 2 2 0.5 , / 2.5 , 1 3.9 , 1 \begin{array}{c|cccc} \hline Y & \delta_1,\Psi_1 & \delta_2,\Psi_2 & \delta_3,\Psi_3 \\ \hline 1 & 1,/ & 2.4,1 & 4.3,2 \\ 2 & 0.5,/ & 2.5,1 & 3.9,1 \\ \hline \end{array} Y12δ1,Ψ11,/0.5,/δ2,Ψ22.4,12.5,1δ3,Ψ34.3,23.9,1
因此最优标记序列为 y ∗ = ( 1 , 2 , 1 ) y^\ast=(1,2,1) y∗=(1,2,1) ;

![[vmware]vmware虚拟机压缩空间清理空间](https://img-blog.csdnimg.cn/a7626de85a264efaa9c957df09fa6f43.png)