分治法——找众数-编程知识

分治法——找众数

要求：

寻找整数数组的众数，如果存在多个众数，则返回权值最小的那个

第一步：

要利用分治法找众数，首先就先要使数组有序。这里，我们用C语言库中的qsort进行快排：

qsort(nums, numsSize, sizeof(int), cmp_int);
//nums——给定数组
//numsSize——数组大小
//cmp_int——qsort要用到的函数指针

第二步：

开始编写分治算法，寻找众数。

函数声明：

void Find_Mode(int* nums, int begin, int end)

为了方便，我们先定义两个全局变量mode_count和mode_index来记录众数出现的次数和下标

int mode_count = 0;	//记录众数出现的次数
int mode_index = 0;	//记录下标

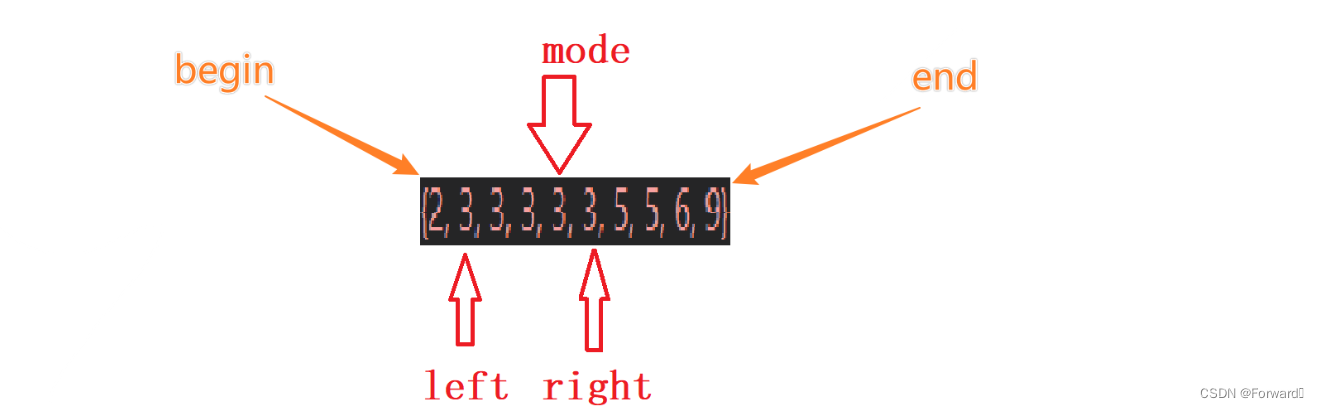
我们以下面的有序数组为例：

在这里插入图片描述

首先假设众数为数组中间的数，记其下标为mode。
int left = begin;
int right = end;
int mode = (right - left) / 2 + left;	//为防止整形移除，故不采用(right + left)/2的写法
然后，移动left和right，确定有多少个值为nums[mode]的元素：
while (left < right && nums[left] != nums[mode])left++;
while (left < right && nums[right] != nums[mode])right--;//这样，值为nums[mode]的元素个数为(right - left + 1)
当确定好nums[mode]的个数count后，就需要比较[begin, left - 1]和[right + 1, end]这两个区间的和count的大小

如果[begin, left - 1]区间的大小大于或等于count就说明该区间内可能出现出现次数更多的或者权值更小的众数。因此要继续进行递归分治。
对于区间[right + 1, end]同理。
if (left - begin >= right - left + 1)Find_Mode(nums, begin, left - 1);if (end - right >= right - left + 1)Find_Mode(nums, right + 1, end);
如果上面两个if语句没有执行，那就说明nums[mode]出现的次数count就是最大的，那就需要和mode_count(众数出现的次数)进行比较

如果count == mode_count。那就比较nums[mode]和nums[mode_index]的权值，并将众数更新为权值较小的那个，并更新mode_index
如果count > mode_count。那就直接让众数为nums[mode]，更新mode_count和mode_index
如果count < mode_cout。就不做任何修改
//right - left + 1即上文所说的count
if (mode_count <= right - left + 1)
{//如果二者相等，就取权值较小的if (mode_count == right - left + 1)mode_index = nums[mode] < nums[mode_index] ? mode : mode_index;else{mode_index = mode;mode_count = right - left + 1;}
}
函数整体即为：
int mode_count = 0;	//记录众数出现的次数
int mode_index = 0;	//记录下标void Find_Mode(int* nums, int begin, int end)
{int left = begin;int right = end;int mode = (right - left) / 2 + left;//移动做右指针，寻找nums[mode]（假设的众数）的出现次数while (left < right && nums[left] != nums[mode])left++;while (left < right && nums[right] != nums[mode])right--;//如果左右区间的长度大于或者等于nums[mode]（假设的众数）的出现次数//那就进行分治递归if (left - begin >= right - left + 1)Find_Mode(nums, begin, left - 1);if (end - right >= right - left + 1)Find_Mode(nums, right + 1, end);//更新众数if (mode_count <= right - left + 1){//如果二者相等，就取权值较小的if (mode_count == right - left + 1)mode_index = nums[mode] < nums[mode_index] ? mode : mode_index;else{mode_index = mode;mode_count = right - left + 1;}}
}

整体代码：

#include <stdio.h>
#include <stdlib.h>int mode_count = 0;	//记录众数出现的次数
int mode_index = 0;	//记录下标void Find_Mode(int* nums, int begin, int end)
{int left = begin;int right = end;int mode = (right - left) / 2 + left;//移动做右指针，寻找nums[mode]（假设的众数）的出现次数while (left < right && nums[left] != nums[mode])left++;while (left < right && nums[right] != nums[mode])right--;//如果左右区间的长度大于或者等于nums[mode]（假设的众数）的出现次数//那就进行分治递归if (left - begin >= right - left + 1)Find_Mode(nums, begin, left - 1);if (end - right >= right - left + 1)Find_Mode(nums, right + 1, end);//更新众数if (mode_count <= right - left + 1){//如果二者相等，就取权值较小的if (mode_count == right - left + 1)mode_index = nums[mode] < nums[mode_index] ? mode : mode_index;else{mode_index = mode;mode_count = right - left + 1;}}
}//qsort需要的函数
int cmp_int(void const* num1, void const* num2)
{return *(int*)num1 - *(int*)num2;
}int main()
{int nums[] = { 10, 4, 2, 10, 5, 8, 9, 5, 6, 1, 4, 7, 2, 1, 7, 4, 3, 1, 7, 2 };int numsSize = sizeof(nums) / sizeof(int);qsort(nums, numsSize, sizeof(int), cmp_int);	//利用快速排序排序数组，是数组升序排列Find_Mode(nums, 0, numsSize - 1);	//找众数printf("众数为：%d\n", nums[mode_index]);return 0;
}