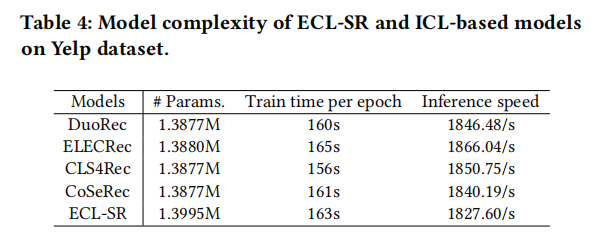
卡尔曼滤波之二:Python实现
- 1.背景描述
- 2.构建卡尔曼滤波公式
- 2.1 预测
- 2.2 更新
- 3.代码实现
- 3.1 输入值
- 3.2 pykalman包实现
- 3.3 不使用Python包实现
- 3.4 效果可视化
- 参考文献
了解了卡尔曼滤波之一:基本概念,可以结合代码来理解下卡尔曼滤波的2个预测+3个更新环节。
1.背景描述
设有一个球在30m的起始高度,以10m/s的速度竖直上抛,用传感器来跟踪球的高度。
对应于卡尔曼滤波,此系统的状态包括位置 h h h及速度 v v v。
球的高度满足式子:
x t = x t − 1 + v t − 1 τ − 1 2 g τ 2 \qquad x_t = x_{t-1} + v_{t-1}\tau - \frac{1}{2} g \tau^2 xt=xt−1+vt−1τ−21gτ2
速度满足:
v t = v t − 1 − g τ \qquad v_t = v_{t-1} - g \tau vt=vt−1−gτ
其中, τ \tau τ 为 t − 1 t-1 t−1 与 t t t之间的时间(s), g g g 为重力加速度。
传感器检测高度,存在的位置协方差约为3m。
2.构建卡尔曼滤波公式
2.1 预测
- 状态值预测
x ^ t − = F ⋅ x ^ t − 1 + B ⋅ u t − 1 ① \qquad\qquad\quad \hat x_t^-=F\cdot\hat x_{t-1} + B\cdot u_{t-1}\qquad\qquad \qquad\qquad \qquad\qquad \quad\ \ \ ① x^t−=F⋅x^t−1+B⋅ut−1 ①
[ h t − v t − ] = [ 1 τ 0 1 ] [ h t − 1 v t − 1 ] + [ − 1 2 τ 2 − τ ] ⋅ g \qquad\qquad\begin{bmatrix} h_t^-\\v_t^-\end{bmatrix} =\begin{bmatrix} 1& \tau \\0 & 1 \end{bmatrix}\begin{bmatrix} h_{t-1}\\v_{t-1}\end{bmatrix}+\begin{bmatrix} - \frac{1}{2} \tau^2\\- \tau\end{bmatrix}\cdot g [ht−vt−]=[10τ1][ht−1vt−1]+[−21τ2−τ]⋅g
- 状态协方差预测
P t − = F ⋅ P t − 1 ⋅ F T + Q ② \qquad\qquad \quad P_{t}^{-}=F\cdot P_{t-1}\cdot F^{T}+Q\qquad\qquad \qquad\qquad \qquad\qquad \qquad ② Pt−=F⋅Pt−1⋅FT+Q②
\qquad 状态协方差预测值的初始值 P 0 − P_{0}^{-} P0−为 [ 1 0 0 1 ] \begin{bmatrix} 1& 0 \\0 & 1 \end{bmatrix} [1001],过程噪声的协方差 Q Q Q 取 [ 0 0 0 0 ] \begin{bmatrix} 0& 0 \\0 & 0 \end{bmatrix} [0000]。
2.2 更新
- 更新卡尔曼增益 K t K_{t} Kt:
K t = P t − ⋅ H T H ⋅ P t − ⋅ H T + R ③ \qquad\qquad K_{t}=\cfrac {P_{t}^{-} \cdot H^{T}}{H\cdot P_{t}^{-} \cdot H^{T}+R}\qquad\qquad \qquad\qquad \qquad\qquad \qquad\ ③ Kt=H⋅Pt−⋅HT+RPt−⋅HT ③
\qquad 观测矩阵 H H H 这里为 [ 1 0 ] \begin{bmatrix} 1& 0 \end{bmatrix} [10], R R R 为 3.
- 融合状态估计值 x ^ t − \hat x_{t}^{-} x^t−以及观测量 Z t Z_t Zt,更新状态值 x ^ t \hat x_{t} x^t:
x ^ t = x ^ t − + K t ( Z t − H ⋅ x ^ t − ) ④ \qquad\qquad \hat x_{t}=\hat x_{t}^{-}+K_t(Z_t-H\cdot \hat x_{t}^{-})\qquad\qquad \qquad\qquad\qquad \qquad\ ④ x^t=x^t−+Kt(Zt−H⋅x^t−) ④
- 更新状态协方差 P t P_{t} Pt:
P t = ( 1 − K t ⋅ H ) P t − ⑤ \qquad\qquad P_{t}=(1-K_t\cdot H) P_{t}^{-}\qquad\qquad \qquad\qquad\qquad \qquad \qquad\ \ \ \ ⑤ Pt=(1−Kt⋅H)Pt− ⑤
3.代码实现
3.1 输入值
import numpy as np
times = 40
tau = 0.1
actual = -4.9*tau**2*np.arange(times)**2
# Simulate the noisy camera data
sim = actual + 3*np.random.randn(times)# kalman filter parameters
initial_state = np.array([[30],[10]])
initial_current_state_covariance =np.eye(2)
Q = np.zeros((2,2)) # process_noise_covariance
R = 3 # observation_covariance
F=np.array([[1,tau],[0,1]])
B=np.array([[-0.5*tau**2],[-tau]])
U=g=9.8
H=np.array([[1,0]])3.2 pykalman包实现
from pykalman import KalmanFilter
# Set up the filter
kf = KalmanFilter(n_dim_obs=1, n_dim_state=2,initial_state_mean=initial_state.reshape(-1) ,initial_state_covariance=initial_current_state_covariance ,transition_matrices=F,observation_matrices=H,observation_covariance=R,transition_covariance=Q,transition_offsets=[-4.9*tau**2, -9.8*tau])state_means, state_covs = kf.filter(sim)
注意,pykalman包中使用transition_offsets来替代 B ⋅ u t − 1 B\cdot u_{t-1} B⋅ut−1部分。
3.3 不使用Python包实现
current_state_covariance=None
current_state_mean=None
time=0
estimated_signal = []
for measurement in sim:# predictif time==0:# initialize predicted_state_means=initial_statepredicted_state_covariances=initial_current_state_covarianceelse:predicted_state_means = F @ current_state_mean+ B*Upredicted_state_covariances = F @current_state_covariance @F.T + Q# updatekalman_gain = predicted_state_covariances @ H.T @ np.linalg.pinv(H@predicted_state_covariances@H.T + R)current_state_mean = predicted_state_means + kalman_gain * (measurement - H @ predicted_state_means)current_state_covariance = predicted_state_covariances - kalman_gain @ H @ predicted_state_covariancesestimated_signal.append(current_state_mean[0,0])time + =1
3.4 效果可视化
import matplotlib
matplotlib.use("TkAgg")
import matplotlib.pyplot as pltplt.figure(figsize=(12, 6))
plt.plot(range(times), sim, label="Noisy Signal")
plt.plot(range(times), state_means[:,0], label="Kalman Signal1")plt.plot(range(times), estimated_signal, label="Estimated Signal (Kalman Filter)")
plt.legend()
plt.title("Signal Denoising with Kalman Filter")
plt.show(block=True)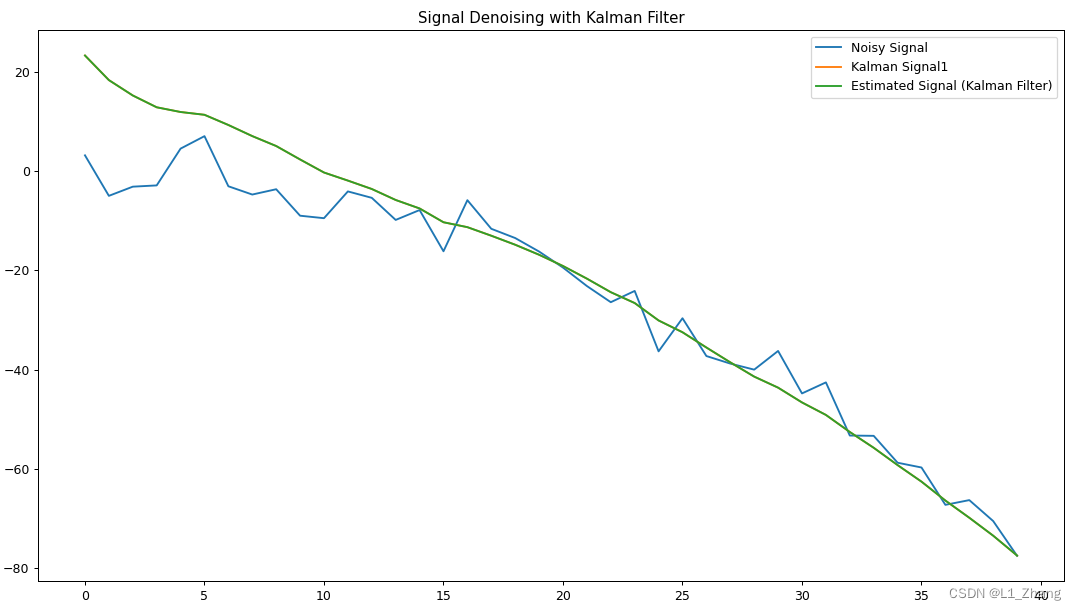
两种方法曲线重合在一起,说明Python实现没有问题。
注意:这里的两种实现都默认t=0时只赋初值,不进行预测。
信号去噪之卡尔曼滤波代码实现中,t=0时也进行了预测。
长期来看,效果差不多,
从图上可以看出,滤波信号与有噪声信号相比,非常平滑,同时也有很好的跟踪效果。
参考文献
[1] 信号去噪之卡尔曼滤波
[2] 卡尔曼滤波:再也不用瑟瑟发抖了
[3] https://github.com/quantopian/research_public/blob/master/notebooks/lectures/Kalman_Filters/notebook.ipynb
[4] https://github.com/pykalman/pykalman/tree/master
[5] https://pykalman.github.io/#choosing-parameters
[6] Kalman Filter and Maximum Likelihood Estimation of Linearized DSGE Models
[7] 卡尔曼滤波之一:基本概念

![Electron[3] 基础配置准备和Electron入门案例](https://img-blog.csdnimg.cn/069302fac6824f2b8c37525b2ef1ab16.png)