一、什么是快速排序算法
快速排序的基本思想是选择一个基准元素(通常选择最后一个元素)将数组分割为两部分,一部分小于基准元素,一部分大于基准元素。
然后递归地对两部分进行排序,直到整个数组有序。这个过程通过 partition 方法实现,它使用两个指针 i 和 j 来遍历数组,将小于基准元素的元素交换到左边,大于基准元素的元素交换到右边。
最后,将基准元素放入正确的位置,并返回该位置作为划分点。快速排序的时间复杂度为O(nlogn)。
如下:快速排序算法的实现代码:
import java.util.Arrays;/*** @Description 快速排序算法**/
public class QuickSort {public static void main(String[] args) {int[] array = {0, 8, 9, 5, 6, 1, 4, 9, 3, 6, 3, 8, 2, 1, 7};quickSort(array, 0, array.length - 1);System.out.println("Sorted array: " + Arrays.toString(array));}// 递归函数用于执行快速排序public static void quickSort(int[] array, int low, int high) {if (low < high) {// 分割数组并获取基准元素的索引int pivotIndex = partition(array, low, high);// 递归排序左侧和右侧子数组quickSort(array, low, pivotIndex - 1);quickSort(array, pivotIndex + 1, high);}}// 函数用于分割数组并返回基准元素的索引public static int partition(int[] array, int low, int high) {// 选择基准元素(在本例中选择最后一个元素)int pivot = array[high];int i = low - 1;// 遍历数组for (int j = low; j < high; j++) {if (array[j] < pivot) {// 如果元素小于基准元素,则交换位置i++;swap(array, i, j);}}// 将基准元素放入正确的位置swap(array, i + 1, high);// 返回基准元素的索引return i + 1;}// 函数用于交换数组中的两个元素public static void swap(int[] array, int i, int j) {int temp = array[i];array[i] = array[j];array[j] = temp;}
}排序输出:
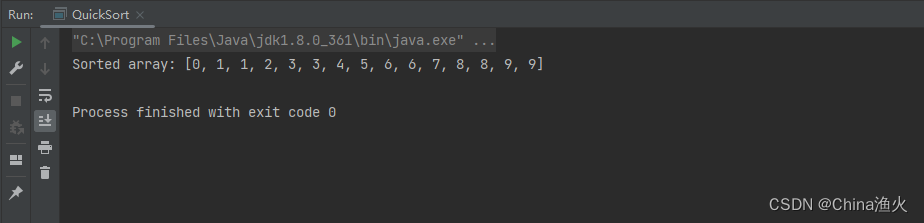
上述代码中,就是快速排序算法的一种实现,总结来说就是:
1. 选择一个基准元素(通常是数组中的最后一个元素)。
2. 将数组分割为两部分,一部分是小于基准元素的元素,另一部分是大于基准元素的元素。
3. 对这两部分分别递归地应用快速排序算法,直到每个子数组都有序。
4. 将所有子数组合并起来,得到最终排序后的数组。
具体步骤实现:
1. 选择基准元素。
2. 设置两个指针,一个指向数组的起始位置(通常为low),另一个指向数组的结束位置(通常为high)。
3. 从起始位置开始,向右移动指针,直到找到一个大于或等于基准元素的元素。
4. 从结束位置开始,向左移动指针,直到找到一个小于或等于基准元素的元素。
5. 如果左指针的位置小于右指针的位置,则交换这两个元素。
6. 重复步骤3到5,直到左指针的位置大于或等于右指针的位置。
7. 将基准元素与左指针所指向的元素进行交换,将基准元素放置在正确的位置。
8. 递归地对基准元素左侧和右侧的子数组应用快速排序算法。
快速排序的关键在于划分过程,即将数组分割为两部分。通过不断地划分和排序,最终实现整个数组的排序。快速排序的平均时间复杂度为O(nlogn),是一种高效的排序算法。
二、快速排序算法和三路快排的关系
快速排序算法和三路快速排序算法都是基于快速排序思想的排序算法,它们之间的关系是三路快速排序算法是对快速排序算法的一种改进和优化。
快速排序算法通过选择一个基准元素,将数组分割为两部分,一部分是小于基准元素的元素,另一部分是大于基准元素的元素。然后递归地对这两部分进行排序,直到整个数组有序。
而三路快速排序算法在快速排序的基础上进行了改进。它通过选择两个基准元素,将数组划分为三部分:小于第一个基准元素、等于第一个基准元素、大于第一个基准元素的元素。然后递归地对小于和大于基准元素的两部分进行排序,而不需要再对等于基准元素的部分进行排序,因为它们已经在正确的位置上。
三路快速排序算法在处理包含大量重复元素的数组时表现更好,因为它能够更有效地处理重复元素,减少了不必要的比较和交换操作。相比于快速排序算法,三路快速排序算法的时间复杂度仍然是O(nlogn),但在某些情况下,它的性能更好。
总的来说,三路快速排序算法是对快速排序算法的改进,通过减少重复元素的比较和交换操作,提高了排序的效率。
三、三路快排代码实现
/*** @Description 三路快排**/
public class ThreeWayQuickSort {public static void main(String[] args) {int[] array = {9, 8, 5, 9, 2, 9, 1, 2, 3, 4, 6, 8, 4, 7};quickSort(array, 0, array.length - 1);System.out.println("排序后的数组:");for (int num : array) {System.out.print(num + " ");}}// 三路快速排序算法public static void quickSort(int[] array, int low, int high) {if (low < high) {// 将数组划分为三部分,并返回等于pivot值的范围int[] range = partition(array, low, high);// 递归地对小于pivot和大于pivot的部分进行排序quickSort(array, low, range[0] - 1);quickSort(array, range[1] + 1, high);}}// 划分数组为三部分的函数public static int[] partition(int[] array, int low, int high) {int pivot = array[low]; // 选择第一个元素作为pivotint lt = low; // 初始化lt指针指向lowint gt = high; // 初始化gt指针指向highint i = low + 1; // 初始化i指针指向low的下一个位置while (i <= gt) {if (array[i] < pivot) {swap(array, i, lt);i++;lt++;} else if (array[i] > pivot) {swap(array, i, gt);gt--;} else {i++;}}// 返回等于pivot值的范围int[] range = {lt, gt};return range;}// 交换数组中两个元素的函数public static void swap(int[] array, int i, int j) {int temp = array[i];array[i] = array[j];array[j] = temp;}
}排序输出:
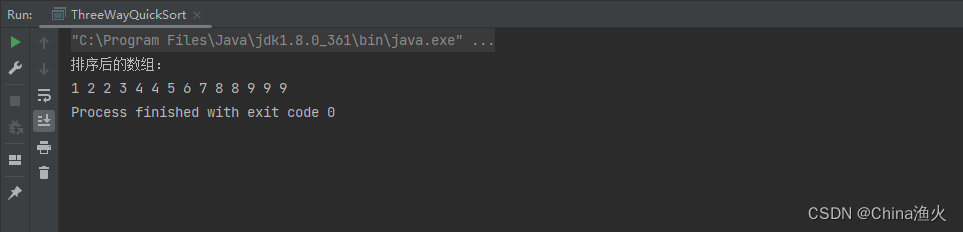
三路快速排序算法是一种高效的排序算法,它通过将数组划分为三个部分来进行排序:
小于pivot的部分、等于pivot的部分和大于pivot的部分。
下面是三路快速排序算法的实现思路步骤总结:
1. 选择一个pivot元素(通常选择数组的第一个元素)。
2. 初始化三个指针:lt指向数组的起始位置,gt指向数组的结束位置,i指向数组的起始位置的下一个位置。
3. 从i开始遍历数组,比较当前元素与pivot的大小关系:
- 如果当前元素小于pivot,将它与lt指针指向的元素交换,并将lt和i指针都向右移动一位。
- 如果当前元素大于pivot,将它与gt指针指向的元素交换,并将gt指针向左移动一位。
- 如果当前元素等于pivot,将i指针向右移动一位。
4. 重复步骤3,直到i指针遍历完整个数组。
5. 最终,数组将被划分为三个部分:小于pivot的部分、等于pivot的部分和大于pivot的部分。
6. 递归地对小于pivot和大于pivot的部分进行三路快速排序。
三路快排算法通过将相等的元素放在中间,这样就避免了重复比较和交换的过程,从而提高了排序的效率。
![[java进阶]——方法引用改写Lambda表达式](https://img-blog.csdnimg.cn/fa211daacd9e4c36a392ab62b9592444.png)