引言
在原神的世界中,小森决定挑战自我,踏上了寻找风神的迷宫——风之迷宫。这个迷宫就像是一个巨大的电玩城,让小森感到困惑和无助。他站在迷宫的入口,看着眼前乱糟糟的路径,内心充满了不安和焦虑。
“派蒙,我… 我真的不知道该怎么办了。”小森向他的老朋友派蒙诉说。
派蒙看着小森愁眉苦脸的样子,笑着说:“别担心,小森,我们可以利用深度优先搜索来寻找路径。这个算法超级强大,它会帮助我们找到一条通往风神的正确道路。”
小森听后有些疑惑,他挠了挠头,瞪大了眼睛问:“深度优先搜索?那是什么?听起来好像很高级的样子。”
派蒙笑着回答:“哈哈,别担心,小森,其实它就像是你吃蛋糕一样。我们从蛋糕的顶部开始,一口一口地吃下去,直到吃到下面为止。这就是深度优先搜索!”
小森听后恍然大悟,“哦!我明白了!就像我们在森林里迷路一样,我们要一直往下走,直到找到出口为止!”
派蒙点点头,“没错,就是这个意思。”
正当他们谈话时,另一位神秘人物小坤出现了。小坤看着小森和派蒙焦虑的样子,笑着说:“你们不必担心迷宫中的路径,我可以给你们提供一种回溯算法,这种算法可以帮助你们在迷宫中寻找路径。回溯算法就像是你走迷宫一样,如果发现走不通,就会原路返回,换一条路继续前进。”
小坤的话让小森和派蒙感到非常安心。他们决定按照小坤的指引行动。在接下来的冒险中,他们分工合作,派蒙利用深度优先搜索算法不断探索迷宫中的路径,而小坤则根据回溯算法不断调整搜索方向,引导他们找到正确的路径。
在探索的过程中,小森想起自己的冒险经历,“派蒙,你说我们会不会像以前一样遇到很多困难呢?”
派蒙看着他,“哈哈,难说呢,小森。但是我们可以抱着乐观的态度去面对。就像以前一样,遇到困难我们就一起解决。”
小森握紧拳头,“好!我相信我们一定能够成功找到风神!”
每当他们遇到困难时,他们都会相互鼓励、互相扶持着继续前进。小坤的回溯算法总是能在关键时刻指引他们走向正确的方向。
通过不断地尝试和探索,他们终于在字符矩阵中找到了通往风神的路径。在这个过程中,他们不仅学会了如何利用深度优先搜索和回溯算法来解决问题,还进一步理解了风神的哲学理念。
最终,当他们站在风神的面前时,小森感慨万分。他向派蒙表示感激:“谢谢你派蒙,如果不是你一直在我身边支持和鼓励我,我可能早就放弃了。”
派蒙笑着回答:“哈哈,别客气,小森!我们是朋友嘛!而且这个冒险旅程也让我学到了很多。”
回溯算法核心思想
回溯:尝试解决问题若某个位置卡着,就回退到那个位置,继续解决计算位置并且确实走那个位置
- 利用深度优先搜索算法不停段的搜索问题
- 若问题有障碍 就回溯到上一个子问题
- 直到解决问题的解
- 在此之上必须定义搜索问题的空间 (防止重复计算)
动态规划算法实现思路
如上所说(引言里) 在字符矩阵里找到包含指定的字符串的路径是否出租
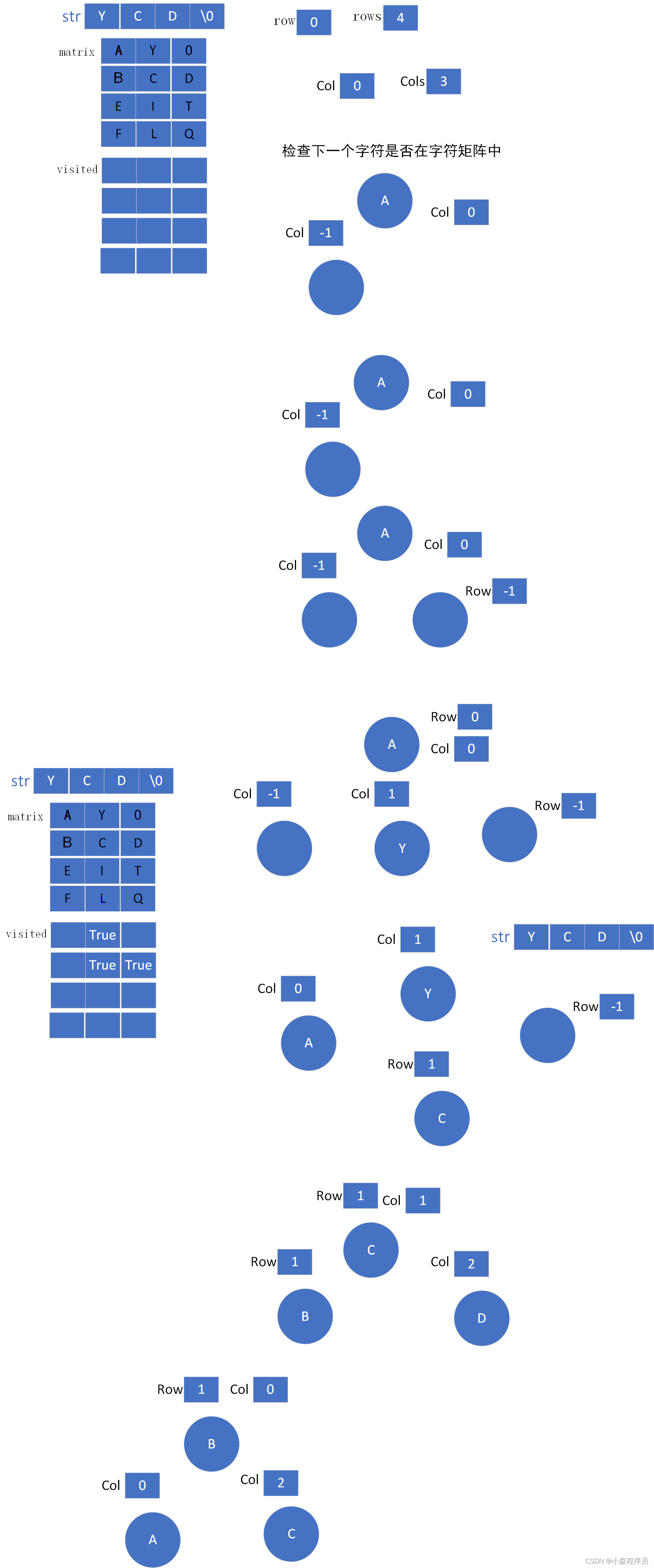
如图 可以看出这搜索的路径 由左上右下策略 走这么一个路径 若都走不动,则回溯并重置路径长度和标记当前字符为未访问过状态,以便其他路径可以继续尝试访问当前字符
虽然说采用递归的方式比较绕 ,但没有必要把 每一个执行的步骤都要做到非常清楚 若是这样动脑能力都没有一点学这个 有啥意思 至于我嘛大概了解 即可没必要死磕 画这个的时候,我需要彻底掌握? 当然需要,但舍近求远 毕竟后面的内容更加精彩 技术更迭 是程序员必备技能
回溯应用算法专区
// 查找字符矩阵中子字符串的路径,返回是否存在路径
bool FindCharMatrixSubstrPath(const char* matrix, int rows, int cols, const char* str) { // 初始化返回值 bool ret = false; // 检查输入矩阵和字符串是否有效,并且行数和列数是否大于1 if (matrix != nullptr && rows > 1 && cols > 1 && str != nullptr) { // 初始化访问数组,用于标记已访问的字符 bool* visited = new bool[rows * cols] {}; // 初始化路径长度为0 int Pathlen = 0; // 遍历矩阵的每个字符 for (size_t row = 0; row < rows; row++) { for (size_t col = 0; col < cols; col++) { // 检查下一个字符是否在字符矩阵路径中 if (CheckNextCharisCharMatrixPath(matrix, rows, cols, row, col, str, Pathlen, visited)) { // 如果找到路径,则设置返回值为true ret = true; // 终止函数执行,并释放访问数组内存 delete[] visited; // 跳出内层循环,继续查找是否有其他路径 break; } } if (ret){ // 如果找到路径,则跳出外层循环,不再继续遍历矩阵 break; } } } // 返回是否存在路径的结果 return ret;
} // 检查下一个字符是否在字符矩阵路径中,返回是否找到路径的结果
bool CheckNextCharisCharMatrixPath(const char* matrix, int rows, int cols, int row, int col, const char* str, int& Pathlen, bool* visited){ // 如果字符串已经遍历完,则返回找到路径的结果 if (str[Pathlen]=='\0'){ return true; } // 初始化是否找到路径的标志为false bool isPath = false;; // 检查当前字符的坐标是否在矩阵范围内 bool CheckRange = row >= 0 && row < rows && col >= 0 && col < cols; // 计算当前字符在矩阵中的索引位置 int matrixIndex = row * cols + col; // 检查当前字符是否与字符串中的字符匹配 bool CheckStr = matrix[matrixIndex] == str[Pathlen]; // 如果坐标在矩阵范围内,字符匹配且未被访问过,则进行递归调用,检查上下左右四个方向是否可以找到路径 if (CheckRange && CheckStr &&!visited[matrixIndex]) { // 更新路径长度并标记当前字符已访问过 Pathlen++; visited[matrixIndex] = true; // 分别检查四个方向是否可以找到路径,任意一个方向可以找到路径,则设置isPath为true,否则回溯并重置路径长度和标记当前字符为未访问过状态 isPath = CheckNextCharisCharMatrixPath(matrix, rows, cols, row , col-1, str, Pathlen, visited) || CheckNextCharisCharMatrixPath(matrix, rows, cols, row -1, col, str, Pathlen, visited) || CheckNextCharisCharMatrixPath(matrix, rows, cols, row, col + 1, str, Pathlen, visited) || CheckNextCharisCharMatrixPath(matrix, rows, cols, row+1, col , str, Pathlen, visited); if (!isPath){ // 如果四个方向都没有找到路径,则回溯并重置路径长度和标记当前字符为未访问过状态,以便其他路径可以继续尝试访问当前字符 Pathlen--; visited[matrixIndex] = false; } } // 返回是否找到路径的结果 return isPath;